Multi-start Optimization Method via Scalarization based on Target Point-based Tchebycheff Distance for Multi-objective Optimization

Multi-objective optimization is crucial in scientific and industrial applications where solutions must balance trade-offs among conflicting objectives. State-of-the-art methods, such as NSGA-III and MOEA/D, can handle many objectives but struggle with coverage issues, particularly in cases involving inverted triangular Pareto fronts or strong nonlinearity. Moreover, NSGA-III often relies on simulated binary crossover, which deteriorates in problems with variable dependencies. In this study, we propose a novel multi-start optimization method that addresses these challenges. Our approach introduces a newly introduced scalarization technique, the Target Point-based Tchebycheff Distance (TPTD) method, which significantly improves coverage on problems with inverted triangular Pareto fronts. For efficient multi-start optimization, TPTD leverages a target point defined in the objective space, which plays a critical role in shaping the scalarized function. The position of the target point is adaptively determined according to the shape of the Pareto front, ensuring improvement in coverage. Furthermore, the flexibility of this scalarization allows seamless integration with powerful single-objective optimization methods, such as natural evolution strategies, to efficiently handle variable dependencies. Experimental results on benchmark problems, including those with inverted triangular Pareto fronts, demonstrate that our method outperforms NSGA-II, NSGA-III, and MOEA/D-DE in terms of the Hypervolume indicator. Notably, our approach achieves computational efficiency improvements of up to 474 times over these baselines.

A Memetic Algorithm based on Variational Autoencoder for Black-Box Discrete Optimization with Epistasis among Parameters

Black-box discrete optimization (BB-DO) problems arise in many real-world applications, such as neural architecture search and mathematical model estimation. A key challenge in BB-DO is epistasis among parameters where multiple variables must be modified simultaneously to effectively improve the objective function. Estimation of Distribution Algorithms (EDAs) provide a powerful framework for tackling BB-DO problems. In particular, an EDA leveraging a Variational Autoencoder (VAE) has demonstrated strong performance on relatively low-dimensional problems with epistasis while reducing computational cost. Meanwhile, evolutionary algorithms such as DSMGA-II and P3, which integrate bit-flip-based local search with linkage learning, have shown excellent performance on high-dimensional problems. In this study, we propose a new memetic algorithm that combines VAE-based sampling with local search. The proposed method inherits the strengths of both VAE-based EDAs and local search-based approaches: it effectively handles high-dimensional problems with epistasis among parameters without incurring excessive computational overhead. Experiments on NK landscapes -- a challenging benchmark for BB-DO involving epistasis among parameters -- demonstrate that our method outperforms state-of-the-art VAE-based EDA methods, as well as leading approaches such as P3 and DSMGA-II.

CatCMA with Margin: Stochastic Optimization for Continuous, Integer, and Categorical Variables

This study focuses on mixed-variable black-box optimization (MV-BBO), addressing continuous, integer, and categorical variables. Many real-world MV-BBO problems involve dependencies among these different types of variables, requiring efficient methods to optimize them simultaneously. Recently, stochastic optimization methods leveraging the mechanism of the covariance matrix adaptation evolution strategy have shown promising results in mixed-integer or mixed-category optimization. However, such methods cannot handle the three types of variables simultaneously. In this study, we propose CatCMA with Margin (CatCMAwM), a stochastic optimization method for MV-BBO that jointly optimizes continuous, integer, and categorical variables. CatCMAwM is developed by incorporating a novel integer handling into CatCMA, a mixed-category black-box optimization method employing a joint distribution of multivariate Gaussian and categorical distributions. The proposed integer handling is carefully designed by reviewing existing integer handlings and following the design principles of CatCMA. Even when applied to mixed-integer problems, it stabilizes the marginal probability and improves the convergence performance of continuous variables. Numerical experiments show that CatCMAwM effectively handles the three types of variables, outperforming state-of-the-art Bayesian optimization methods and baselines that simply incorporate existing integer handlings into CatCMA.

Instance-wise Supervision-level Optimization in Active Learning

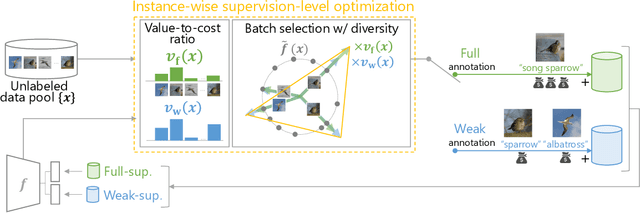
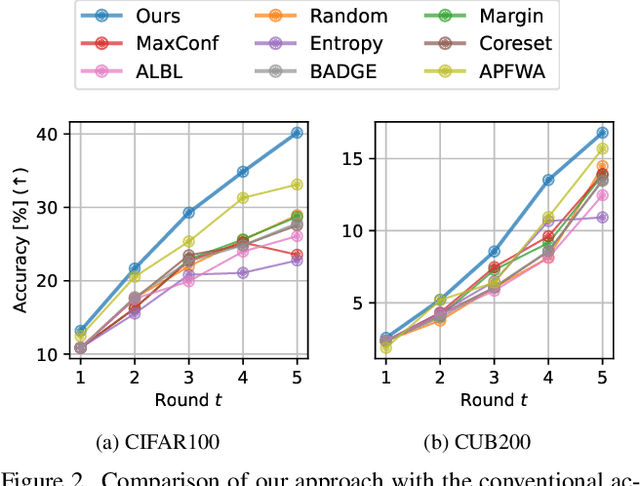
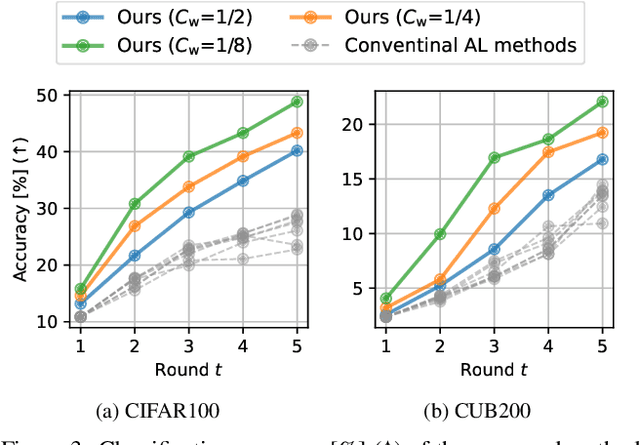
Active learning (AL) is a label-efficient machine learning paradigm that focuses on selectively annotating high-value instances to maximize learning efficiency. Its effectiveness can be further enhanced by incorporating weak supervision, which uses rough yet cost-effective annotations instead of exact (i.e., full) but expensive annotations. We introduce a novel AL framework, Instance-wise Supervision-Level Optimization (ISO), which not only selects the instances to annotate but also determines their optimal annotation level within a fixed annotation budget. Its optimization criterion leverages the value-to-cost ratio (VCR) of each instance while ensuring diversity among the selected instances. In classification experiments, ISO consistently outperforms traditional AL methods and surpasses a state-of-the-art AL approach that combines full and weak supervision, achieving higher accuracy at a lower overall cost. This code is available at https://github.com/matsuo-shinnosuke/ISOAL.

Harnessing the Latent Diffusion Model for Training-Free Image Style Transfer

Diffusion models have recently shown the ability to generate high-quality images. However, controlling its generation process still poses challenges. The image style transfer task is one of those challenges that transfers the visual attributes of a style image to another content image. Typical obstacle of this task is the requirement of additional training of a pre-trained model. We propose a training-free style transfer algorithm, Style Tracking Reverse Diffusion Process (STRDP) for a pretrained Latent Diffusion Model (LDM). Our algorithm employs Adaptive Instance Normalization (AdaIN) function in a distinct manner during the reverse diffusion process of an LDM while tracking the encoding history of the style image. This algorithm enables style transfer in the latent space of LDM for reduced computational cost, and provides compatibility for various LDM models. Through a series of experiments and a user study, we show that our method can quickly transfer the style of an image without additional training. The speed, compatibility, and training-free aspect of our algorithm facilitates agile experiments with combinations of styles and LDMs for extensive application.

CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points

Discrete and mixed-variable optimization problems have appeared in several real-world applications. Most of the research on mixed-variable optimization considers a mixture of integer and continuous variables, and several integer handlings have been developed to inherit the optimization performance of the continuous optimization methods to mixed-integer optimization. In some applications, acceptable solutions are given by selecting possible points in the disjoint subspaces. This paper focuses on the optimization on sets of points and proposes an optimization method by extending the covariance matrix adaptation evolution strategy (CMA-ES), termed the CMA-ES on sets of points (CMA-ES-SoP). The CMA-ES-SoP incorporates margin correction that maintains the generation probability of neighboring points to prevent premature convergence to a specific non-optimal point, which is an effective integer-handling technique for CMA-ES. In addition, because margin correction with a fixed margin value tends to increase the marginal probabilities for a portion of neighboring points more than necessary, the CMA-ES-SoP updates the target margin value adaptively to make the average of the marginal probabilities close to a predefined target probability. Numerical simulations demonstrated that the CMA-ES-SoP successfully optimized the optimization problems on sets of points, whereas the naive CMA-ES failed to optimize them due to premature convergence.

Effective Off-Policy Evaluation and Learning in Contextual Combinatorial Bandits

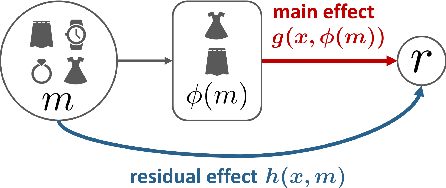
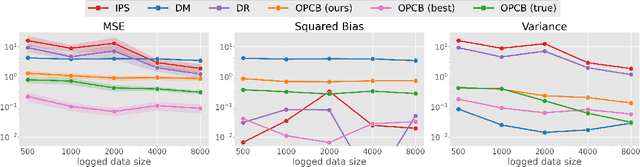
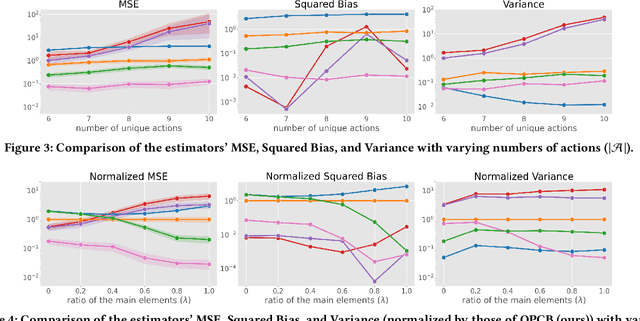
We explore off-policy evaluation and learning (OPE/L) in contextual combinatorial bandits (CCB), where a policy selects a subset in the action space. For example, it might choose a set of furniture pieces (a bed and a drawer) from available items (bed, drawer, chair, etc.) for interior design sales. This setting is widespread in fields such as recommender systems and healthcare, yet OPE/L of CCB remains unexplored in the relevant literature. Typical OPE/L methods such as regression and importance sampling can be applied to the CCB problem, however, they face significant challenges due to high bias or variance, exacerbated by the exponential growth in the number of available subsets. To address these challenges, we introduce a concept of factored action space, which allows us to decompose each subset into binary indicators. This formulation allows us to distinguish between the ''main effect'' derived from the main actions, and the ''residual effect'', originating from the supplemental actions, facilitating more effective OPE. Specifically, our estimator, called OPCB, leverages an importance sampling-based approach to unbiasedly estimate the main effect, while employing regression-based approach to deal with the residual effect with low variance. OPCB achieves substantial variance reduction compared to conventional importance sampling methods and bias reduction relative to regression methods under certain conditions, as illustrated in our theoretical analysis. Experiments demonstrate OPCB's superior performance over typical methods in both OPE and OPL.

Natural Gradient Interpretation of Rank-One Update in CMA-ES

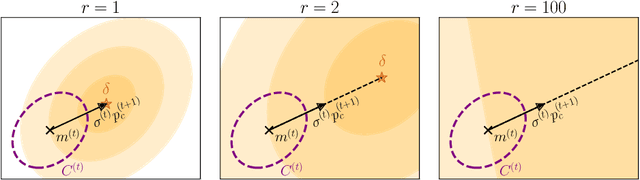
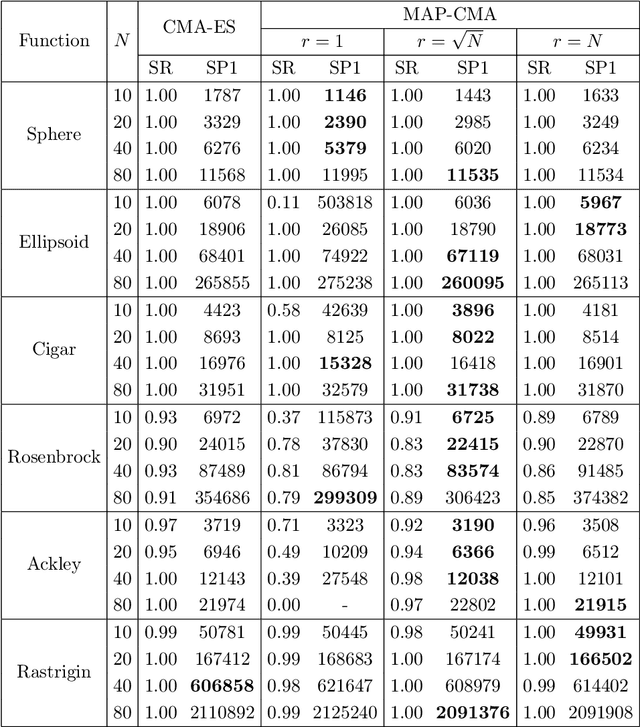
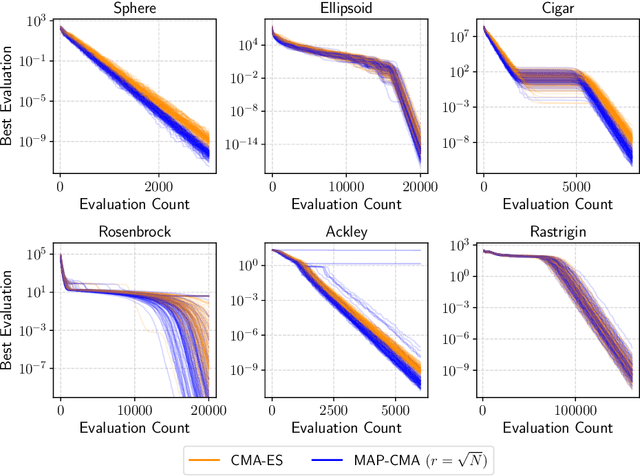
The covariance matrix adaptation evolution strategy (CMA-ES) is a stochastic search algorithm using a multivariate normal distribution for continuous black-box optimization. In addition to strong empirical results, part of the CMA-ES can be described by a stochastic natural gradient method and can be derived from information geometric optimization (IGO) framework. However, there are some components of the CMA-ES, such as the rank-one update, for which the theoretical understanding is limited. While the rank-one update makes the covariance matrix to increase the likelihood of generating a solution in the direction of the evolution path, this idea has been difficult to formulate and interpret as a natural gradient method unlike the rank-$\mu$ update. In this work, we provide a new interpretation of the rank-one update in the CMA-ES from the perspective of the natural gradient with prior distribution. First, we propose maximum a posteriori IGO (MAP-IGO), which is the IGO framework extended to incorporate a prior distribution. Then, we derive the rank-one update from the MAP-IGO by setting the prior distribution based on the idea that the promising mean vector should exist in the direction of the evolution path. Moreover, the newly derived rank-one update is extensible, where an additional term appears in the update for the mean vector. We empirically investigate the properties of the additional term using various benchmark functions.

CMA-ES for Safe Optimization

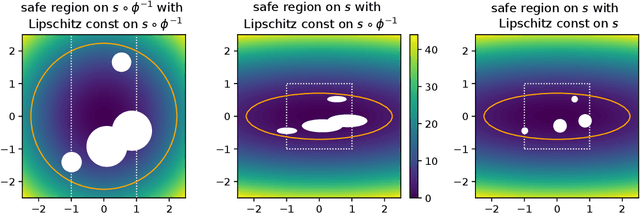
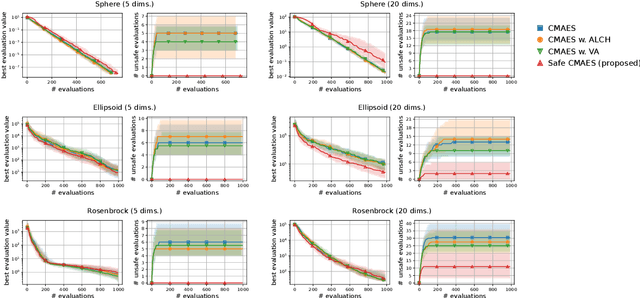
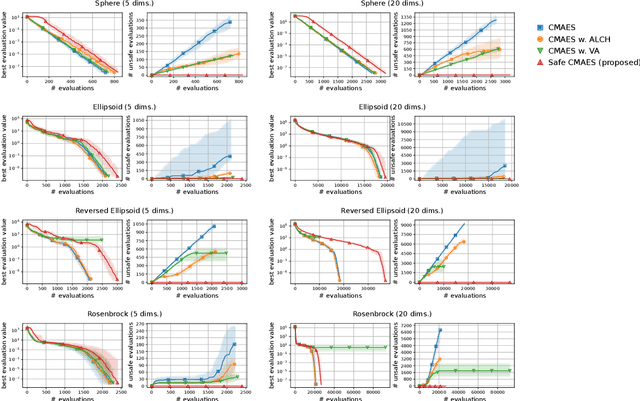
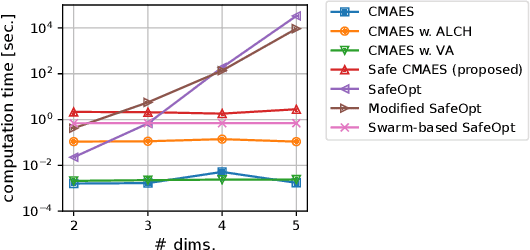
In several real-world applications in medical and control engineering, there are unsafe solutions whose evaluations involve inherent risk. This optimization setting is known as safe optimization and formulated as a specialized type of constrained optimization problem with constraints for safety functions. Safe optimization requires performing efficient optimization without evaluating unsafe solutions. A few studies have proposed the optimization methods for safe optimization based on Bayesian optimization and the evolutionary algorithm. However, Bayesian optimization-based methods often struggle to achieve superior solutions, and the evolutionary algorithm-based method fails to effectively reduce unsafe evaluations. This study focuses on CMA-ES as an efficient evolutionary algorithm and proposes an optimization method termed safe CMA-ES. The safe CMA-ES is designed to achieve both safety and efficiency in safe optimization. The safe CMA-ES estimates the Lipschitz constants of safety functions transformed with the distribution parameters using the maximum norm of the gradient in Gaussian process regression. Subsequently, the safe CMA-ES projects the samples to the nearest point in the safe region constructed with the estimated Lipschitz constants. The numerical simulation using the benchmark functions shows that the safe CMA-ES successfully performs optimization, suppressing the unsafe evaluations, while the existing methods struggle to significantly reduce the unsafe evaluations.

CatCMA : Stochastic Optimization for Mixed-Category Problems

Black-box optimization problems often require simultaneously optimizing different types of variables, such as continuous, integer, and categorical variables. Unlike integer variables, categorical variables do not necessarily have a meaningful order, and the discretization approach of continuous variables does not work well. Although several Bayesian optimization methods can deal with mixed-category black-box optimization (MC-BBO), they suffer from a lack of scalability to high-dimensional problems and internal computational cost. This paper proposes CatCMA, a stochastic optimization method for MC-BBO problems, which employs the joint probability distribution of multivariate Gaussian and categorical distributions as the search distribution. CatCMA updates the parameters of the joint probability distribution in the natural gradient direction. CatCMA also incorporates the acceleration techniques used in the covariance matrix adaptation evolution strategy (CMA-ES) and the stochastic natural gradient method, such as step-size adaptation and learning rate adaptation. In addition, we restrict the ranges of the categorical distribution parameters by margin to prevent premature convergence and analytically derive a promising margin setting. Numerical experiments show that the performance of CatCMA is superior and more robust to problem dimensions compared to state-of-the-art Bayesian optimization algorithms.