CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points

Discrete and mixed-variable optimization problems have appeared in several real-world applications. Most of the research on mixed-variable optimization considers a mixture of integer and continuous variables, and several integer handlings have been developed to inherit the optimization performance of the continuous optimization methods to mixed-integer optimization. In some applications, acceptable solutions are given by selecting possible points in the disjoint subspaces. This paper focuses on the optimization on sets of points and proposes an optimization method by extending the covariance matrix adaptation evolution strategy (CMA-ES), termed the CMA-ES on sets of points (CMA-ES-SoP). The CMA-ES-SoP incorporates margin correction that maintains the generation probability of neighboring points to prevent premature convergence to a specific non-optimal point, which is an effective integer-handling technique for CMA-ES. In addition, because margin correction with a fixed margin value tends to increase the marginal probabilities for a portion of neighboring points more than necessary, the CMA-ES-SoP updates the target margin value adaptively to make the average of the marginal probabilities close to a predefined target probability. Numerical simulations demonstrated that the CMA-ES-SoP successfully optimized the optimization problems on sets of points, whereas the naive CMA-ES failed to optimize them due to premature convergence.

Tail Bounds on the Runtime of Categorical Compact Genetic Algorithm

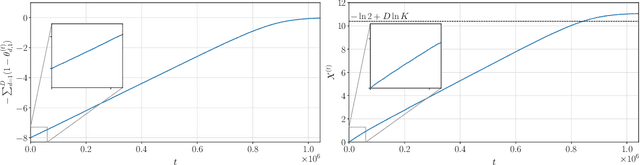
The majority of theoretical analyses of evolutionary algorithms in the discrete domain focus on binary optimization algorithms, even though black-box optimization on the categorical domain has a lot of practical applications. In this paper, we consider a probabilistic model-based algorithm using the family of categorical distributions as its underlying distribution and set the sample size as two. We term this specific algorithm the categorical compact genetic algorithm (ccGA). The ccGA can be considered as an extension of the compact genetic algorithm (cGA), which is an efficient binary optimization algorithm. We theoretically analyze the dependency of the number of possible categories $K$, the number of dimensions $D$, and the learning rate $\eta$ on the runtime. We investigate the tail bound of the runtime on two typical linear functions on the categorical domain: categorical OneMax (COM) and KVal. We derive that the runtimes on COM and KVal are $O(\sqrt{D} \ln (DK) / \eta)$ and $\Theta(D \ln K/ \eta)$ with high probability, respectively. Our analysis is a generalization for that of the cGA on the binary domain.

CMA-ES with Adaptive Reevaluation for Multiplicative Noise

The covariance matrix adaptation evolution strategy (CMA-ES) is a powerful optimization method for continuous black-box optimization problems. Several noise-handling methods have been proposed to bring out the optimization performance of the CMA-ES on noisy objective functions. The adaptations of the population size and the learning rate are two major approaches that perform well under additive Gaussian noise. The reevaluation technique is another technique that evaluates each solution multiple times. In this paper, we discuss the difference between those methods from the perspective of stochastic relaxation that considers the maximization of the expected utility function. We derive that the set of maximizers of the noise-independent utility, which is used in the reevaluation technique, certainly contains the optimal solution, while the noise-dependent utility, which is used in the population size and leaning rate adaptations, does not satisfy it under multiplicative noise. Based on the discussion, we develop the reevaluation adaptation CMA-ES (RA-CMA-ES), which computes two update directions using half of the evaluations and adapts the number of reevaluations based on the estimated correlation of those two update directions. The numerical simulation shows that the RA-CMA-ES outperforms the comparative method under multiplicative noise, maintaining competitive performance under additive noise.

CMA-ES for Safe Optimization

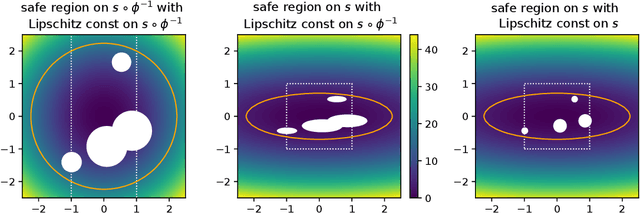
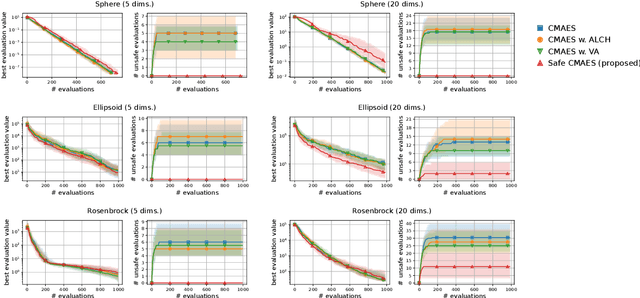
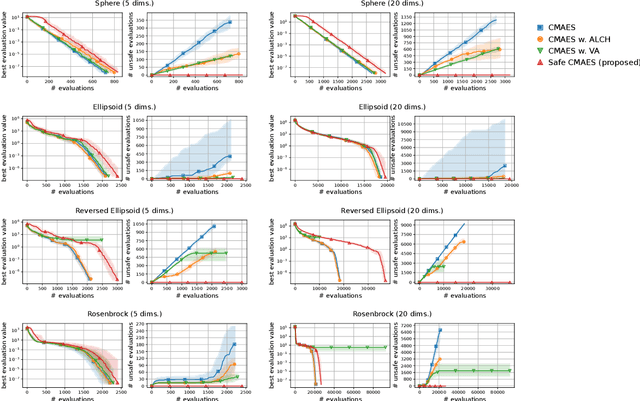
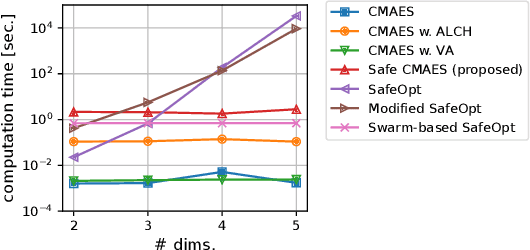
In several real-world applications in medical and control engineering, there are unsafe solutions whose evaluations involve inherent risk. This optimization setting is known as safe optimization and formulated as a specialized type of constrained optimization problem with constraints for safety functions. Safe optimization requires performing efficient optimization without evaluating unsafe solutions. A few studies have proposed the optimization methods for safe optimization based on Bayesian optimization and the evolutionary algorithm. However, Bayesian optimization-based methods often struggle to achieve superior solutions, and the evolutionary algorithm-based method fails to effectively reduce unsafe evaluations. This study focuses on CMA-ES as an efficient evolutionary algorithm and proposes an optimization method termed safe CMA-ES. The safe CMA-ES is designed to achieve both safety and efficiency in safe optimization. The safe CMA-ES estimates the Lipschitz constants of safety functions transformed with the distribution parameters using the maximum norm of the gradient in Gaussian process regression. Subsequently, the safe CMA-ES projects the samples to the nearest point in the safe region constructed with the estimated Lipschitz constants. The numerical simulation using the benchmark functions shows that the safe CMA-ES successfully performs optimization, suppressing the unsafe evaluations, while the existing methods struggle to significantly reduce the unsafe evaluations.

CatCMA : Stochastic Optimization for Mixed-Category Problems

Black-box optimization problems often require simultaneously optimizing different types of variables, such as continuous, integer, and categorical variables. Unlike integer variables, categorical variables do not necessarily have a meaningful order, and the discretization approach of continuous variables does not work well. Although several Bayesian optimization methods can deal with mixed-category black-box optimization (MC-BBO), they suffer from a lack of scalability to high-dimensional problems and internal computational cost. This paper proposes CatCMA, a stochastic optimization method for MC-BBO problems, which employs the joint probability distribution of multivariate Gaussian and categorical distributions as the search distribution. CatCMA updates the parameters of the joint probability distribution in the natural gradient direction. CatCMA also incorporates the acceleration techniques used in the covariance matrix adaptation evolution strategy (CMA-ES) and the stochastic natural gradient method, such as step-size adaptation and learning rate adaptation. In addition, we restrict the ranges of the categorical distribution parameters by margin to prevent premature convergence and analytically derive a promising margin setting. Numerical experiments show that the performance of CatCMA is superior and more robust to problem dimensions compared to state-of-the-art Bayesian optimization algorithms.

-CMA-ES with Margin for Discrete and Mixed-Integer Problems

The covariance matrix adaptation evolution strategy (CMA-ES) is an efficient continuous black-box optimization method. The CMA-ES possesses many attractive features, including invariance properties and a well-tuned default hyperparameter setting. Moreover, several components to specialize the CMA-ES have been proposed, such as noise handling and constraint handling. To utilize these advantages in mixed-integer optimization problems, the CMA-ES with margin has been proposed. The CMA-ES with margin prevents the premature convergence of discrete variables by the margin correction, in which the distribution parameters are modified to leave the generation probability for changing the discrete variable. The margin correction has been applied to ($\mu/\mu_\mathrm{w}$,$\lambda$)-CMA-ES, while this paper introduces the margin correction into (1+1)-CMA-ES, an elitist version of CMA-ES. The (1+1)-CMA-ES is often advantageous for unimodal functions and can be computationally less expensive. To tackle the performance deterioration on mixed-integer optimization, we use the discretized elitist solution as the mean of the sampling distribution and modify the margin correction not to move the elitist solution. The numerical simulation using benchmark functions on mixed-integer, integer, and binary domains shows that (1+1)-CMA-ES with margin outperforms the CMA-ES with margin and is better than or comparable with several specialized methods to a particular search domain.

Adaptive Stochastic Natural Gradient Method for One-Shot Neural Architecture Search

High sensitivity of neural architecture search (NAS) methods against their input such as step-size (i.e., learning rate) and search space prevents practitioners from applying them out-of-the-box to their own problems, albeit its purpose is to automate a part of tuning process. Aiming at a fast, robust, and widely-applicable NAS, we develop a generic optimization framework for NAS. We turn a coupled optimization of connection weights and neural architecture into a differentiable optimization by means of stochastic relaxation. It accepts arbitrary search space (widely-applicable) and enables to employ a gradient-based simultaneous optimization of weights and architecture (fast). We propose a stochastic natural gradient method with an adaptive step-size mechanism built upon our theoretical investigation (robust). Despite its simplicity and no problem-dependent parameter tuning, our method exhibited near state-of-the-art performances with low computational budgets both on image classification and inpainting tasks.