Challenges of Interaction in Optimizing Mixed Categorical-Continuous Variables

Optimization of mixed categorical-continuous variables is prevalent in real-world applications of black-box optimization. Recently, CatCMA has been proposed as a method for optimizing such variables and has demonstrated success in hyper-parameter optimization problems. However, it encounters challenges when optimizing categorical variables in the presence of interaction between continuous and categorical variables in the objective function. In this paper, we focus on optimizing mixed binary-continuous variables as a special case and identify two types of variable interactions that make the problem particularly challenging for CatCMA. To address these difficulties, we propose two algorithmic components: a warm-starting strategy and a hyper-representation technique. We analyze their theoretical impact on test problems exhibiting these interaction properties. Empirical results demonstrate that the proposed components effectively address the identified challenges, and CatCMA enhanced with these components, named ICatCMA, outperforms the original CatCMA.

Tail Bounds on the Runtime of Categorical Compact Genetic Algorithm

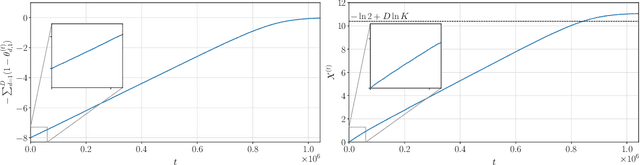
The majority of theoretical analyses of evolutionary algorithms in the discrete domain focus on binary optimization algorithms, even though black-box optimization on the categorical domain has a lot of practical applications. In this paper, we consider a probabilistic model-based algorithm using the family of categorical distributions as its underlying distribution and set the sample size as two. We term this specific algorithm the categorical compact genetic algorithm (ccGA). The ccGA can be considered as an extension of the compact genetic algorithm (cGA), which is an efficient binary optimization algorithm. We theoretically analyze the dependency of the number of possible categories $K$, the number of dimensions $D$, and the learning rate $\eta$ on the runtime. We investigate the tail bound of the runtime on two typical linear functions on the categorical domain: categorical OneMax (COM) and KVal. We derive that the runtimes on COM and KVal are $O(\sqrt{D} \ln (DK) / \eta)$ and $\Theta(D \ln K/ \eta)$ with high probability, respectively. Our analysis is a generalization for that of the cGA on the binary domain.

Theoretical Analysis of Explicit Averaging and Novel Sign Averaging in Comparison-Based Search

In black-box optimization, noise in the objective function is inevitable. Noise disrupts the ranking of candidate solutions in comparison-based optimization, possibly deteriorating the search performance compared with a noiseless scenario. Explicit averaging takes the sample average of noisy objective function values and is widely used as a simple and versatile noise-handling technique. Although it is suitable for various applications, it is ineffective if the mean is not finite. We theoretically reveal that explicit averaging has a negative effect on the estimation of ground-truth rankings when assuming stably distributed noise without a finite mean. Alternatively, sign averaging is proposed as a simple but robust noise-handling technique. We theoretically prove that the sign averaging estimates the order of the medians of the noisy objective function values of a pair of points with arbitrarily high probability as the number of samples increases. Its advantages over explicit averaging and its robustness are also confirmed through numerical experiments.

Convergence rate of the -evolution strategy on locally strongly convex functions with lipschitz continuous gradient and their monotonic transformations

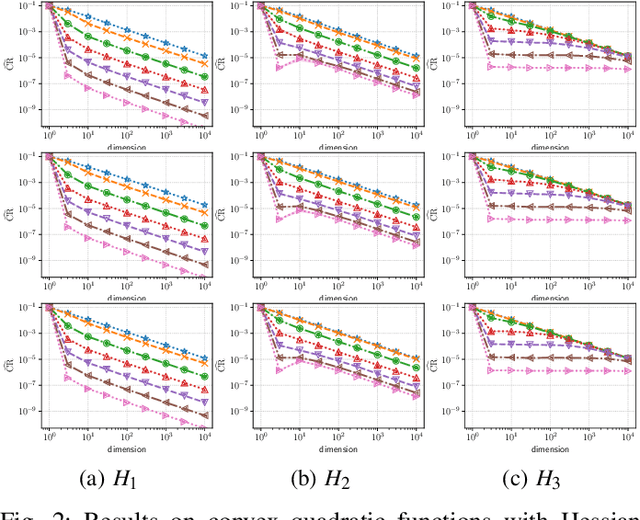
Evolution strategy (ES) is one of promising classes of algorithms for black-box continuous optimization. Despite its broad successes in applications, theoretical analysis on the speed of its convergence is limited on convex quadratic functions and their monotonic transformation. In this study, an upper bound and a lower bound of the rate of linear convergence of the (1+1)-ES on locally $L$-strongly convex functions with $U$-Lipschitz continuous gradient are derived as $\exp\left(-\Omega_{d\to\infty}\left(\frac{L}{d\cdot U}\right)\right)$ and $\exp\left(-\frac1d\right)$, respectively. Notably, any prior knowledge on the mathematical properties of the objective function such as Lipschitz constant is not given to the algorithm, whereas the existing analyses of derivative-free optimization algorithms require them.

Convergence Rate of the -Evolution Strategy with Success-Based Step-Size Adaptation on Convex Quadratic Functions

The (1+1)-evolution strategy (ES) with success-based step-size adaptation is analyzed on a general convex quadratic function and its monotone transformation, that is, $f(x) = g((x - x^*)^\mathrm{T} H (x - x^*))$, where $g:\mathbb{R}\to\mathbb{R}$ is a strictly increasing function, $H$ is a positive-definite symmetric matrix, and $x^* \in \mathbb{R}^d$ is the optimal solution of $f$. The convergence rate, that is, the decrease rate of the distance from a search point $m_t$ to the optimal solution $x^*$, is proven to be in $O(\exp( - L / \mathrm{Tr}(H) ))$, where $L$ is the smallest eigenvalue of $H$ and $\mathrm{Tr}(H)$ is the trace of $H$. This result generalizes the known rate of $O(\exp(- 1/d ))$ for the case of $H = I_{d}$ ($I_d$ is the identity matrix of dimension $d$) and $O(\exp(- 1/ (d\cdot\xi) ))$ for the case of $H = \mathrm{diag}(\xi \cdot I_{d/2}, I_{d/2})$. To the best of our knowledge, this is the first study in which the convergence rate of the (1+1)-ES is derived explicitly and rigorously on a general convex quadratic function, which depicts the impact of the distribution of the eigenvalues in the Hessian $H$ on the optimization and not only the impact of the condition number of $H$.