Variational Bayesian Methods for a Tree-Structured Stick-Breaking Process Mixture of Gaussians

The Bayes coding algorithm for context tree source is a successful example of Bayesian tree estimation in text compression in information theory. This algorithm provides an efficient parametric representation of the posterior tree distribution and exact updating of its parameters. We apply this algorithm to a clustering task in machine learning. More specifically, we apply it to Bayesian estimation of the tree-structured stick-breaking process (TS-SBP) mixture models. For TS-SBP mixture models, only Markov chain Monte Carlo methods have been proposed so far, but any variational Bayesian methods have not been proposed yet. In this paper, we propose a variational Bayesian method that has a subroutine similar to the Bayes coding algorithm for context tree sources. We confirm its behavior by a numerical experiment on a toy example.

An Algorithmic Framework for Constructing Multiple Decision Trees by Evaluating Their Combination Performance Throughout the Construction Process

Predictions using a combination of decision trees are known to be effective in machine learning. Typical ideas for constructing a combination of decision trees for prediction are bagging and boosting. Bagging independently constructs decision trees without evaluating their combination performance and averages them afterward. Boosting constructs decision trees sequentially, only evaluating a combination performance of a new decision tree and the fixed past decision trees at each step. Therefore, neither method directly constructs nor evaluates a combination of decision trees for the final prediction. When the final prediction is based on a combination of decision trees, it is natural to evaluate the appropriateness of the combination when constructing them. In this study, we propose a new algorithmic framework that constructs decision trees simultaneously and evaluates their combination performance throughout the construction process. Our framework repeats two procedures. In the first procedure, we construct new candidates of combinations of decision trees to find a proper combination of decision trees. In the second procedure, we evaluate each combination performance of decision trees under some criteria and select a better combination. To confirm the performance of the proposed framework, we perform experiments on synthetic and benchmark data.

Boosting-Based Sequential Meta-Tree Ensemble Construction for Improved Decision Trees

A decision tree is one of the most popular approaches in machine learning fields. However, it suffers from the problem of overfitting caused by overly deepened trees. Then, a meta-tree is recently proposed. It solves the problem of overfitting caused by overly deepened trees. Moreover, the meta-tree guarantees statistical optimality based on Bayes decision theory. Therefore, the meta-tree is expected to perform better than the decision tree. In contrast to a single decision tree, it is known that ensembles of decision trees, which are typically constructed boosting algorithms, are more effective in improving predictive performance. Thus, it is expected that ensembles of meta-trees are more effective in improving predictive performance than a single meta-tree, and there are no previous studies that construct multiple meta-trees in boosting. Therefore, in this study, we propose a method to construct multiple meta-trees using a boosting approach. Through experiments with synthetic and benchmark datasets, we conduct a performance comparison between the proposed methods and the conventional methods using ensembles of decision trees. Furthermore, while ensembles of decision trees can cause overfitting as well as a single decision tree, experiments confirmed that ensembles of meta-trees can prevent overfitting due to the tree depth.

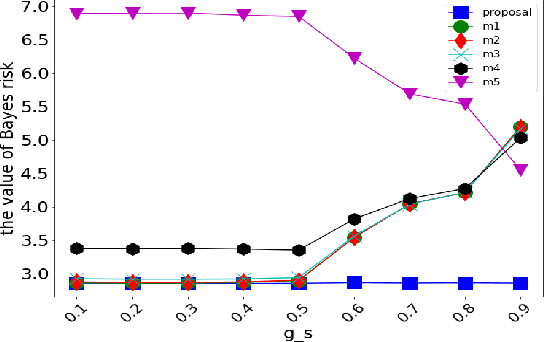
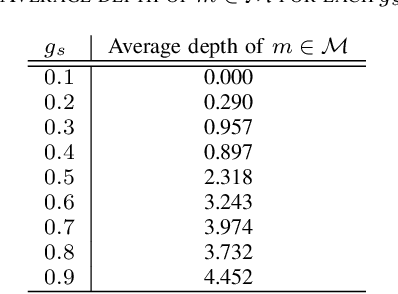
Prediction Algorithms Achieving Bayesian Decision Theoretical Optimality Based on Decision Trees as Data Observation Processes

In the field of decision trees, most previous studies have difficulty ensuring the statistical optimality of a prediction of new data and suffer from overfitting because trees are usually used only to represent prediction functions to be constructed from given data. In contrast, some studies, including this paper, used the trees to represent stochastic data observation processes behind given data. Moreover, they derived the statistically optimal prediction, which is robust against overfitting, based on the Bayesian decision theory by assuming a prior distribution for the trees. However, these studies still have a problem in computing this Bayes optimal prediction because it involves an infeasible summation for all division patterns of a feature space, which is represented by the trees and some parameters. In particular, an open problem is a summation with respect to combinations of division axes, i.e., the assignment of features to inner nodes of the tree. We solve this by a Markov chain Monte Carlo method, whose step size is adaptively tuned according to a posterior distribution for the trees.

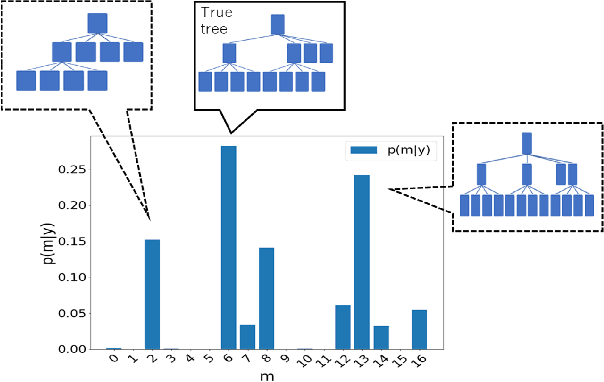
Batch Updating of a Posterior Tree Distribution over a Meta-Tree

Previously, we proposed a probabilistic data generation model represented by an unobservable tree and a sequential updating method to calculate a posterior distribution over a set of trees. The set is called a meta-tree. In this paper, we propose a more efficient batch updating method.

Stochastic 2D Signal Generative Model with Wavelet Packets Basis Regarded as a Random Variable and Bayes Optimal Processing

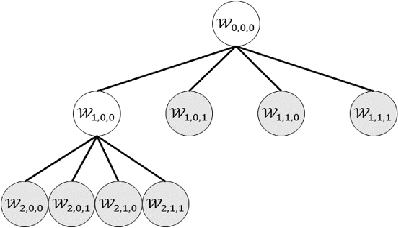
This study deals with two-dimensional (2D) signal processing using the wavelet packet transform. When the basis is unknown the candidate of basis increases in exponential order with respect to the signal size. Previous studies do not consider the basis as a random vaiables. Therefore, the cost function needs to be used to select a basis. However, this method is often a heuristic and a greedy search because it is impossible to search all the candidates for a huge number of bases. Therefore, it is difficult to evaluate the entire signal processing under a criterion and also it does not always gurantee the optimality of the entire signal processing. In this study, we propose a stochastic generative model in which the basis is regarded as a random variable. This makes it possible to evaluate entire signal processing under a unified criterion i.e. Bayes criterion. Moreover we can derive an optimal signal processing scheme that achieves the theoretical limit. This derived scheme shows that all the bases should be combined according to the posterior in stead of selecting a single basis. Although exponential order calculations is required for this scheme, we have derived a recursive algorithm for this scheme, which successfully reduces the computational complexity from the exponential order to the polynomial order.

Probability Distribution on Rooted Trees

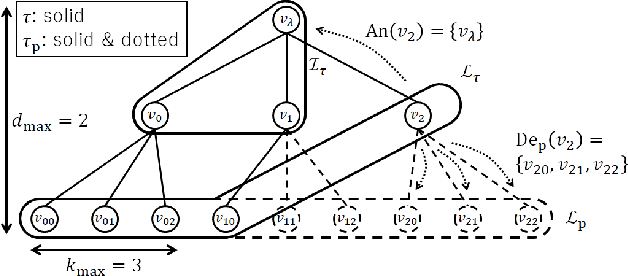
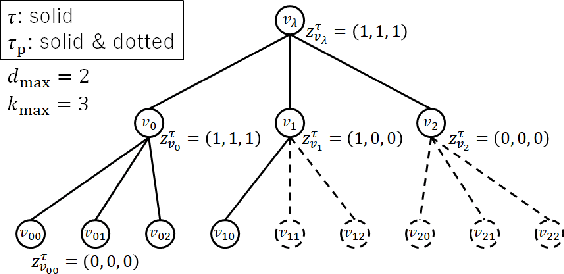
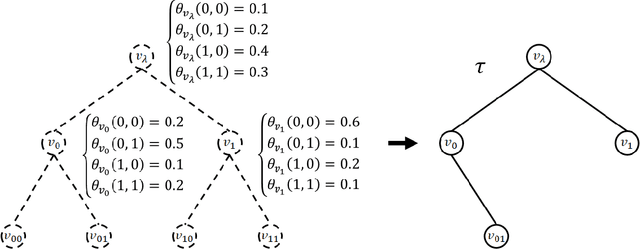
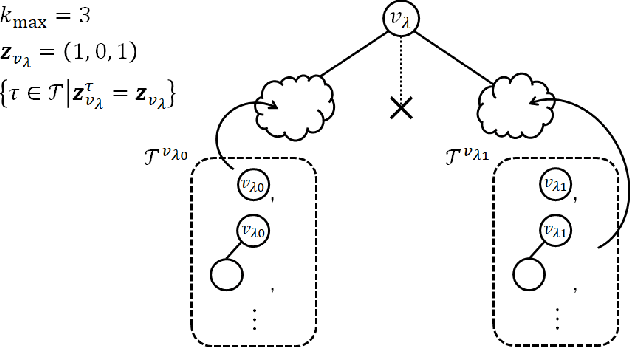
The hierarchical and recursive expressive capability of rooted trees is applicable to represent statistical models in various areas, such as data compression, image processing, and machine learning. On the other hand, such hierarchical expressive capability causes a problem in tree selection to avoid overfitting. One unified approach to solve this is a Bayesian approach, on which the rooted tree is regarded as a random variable and a direct loss function can be assumed on the selected model or the predicted value for a new data point. However, all the previous studies on this approach are based on the probability distribution on full trees, to the best of our knowledge. In this paper, we propose a generalized probability distribution for any rooted trees in which only the maximum number of child nodes and the maximum depth are fixed. Furthermore, we derive recursive methods to evaluate the characteristics of the probability distribution without any approximations.

Probability Distribution on Full Rooted Trees

The recursive and hierarchical structure of full rooted trees is used in various areas such as data compression, image processing, and machine learning. In most of these studies, the full rooted tree is not a random variable. It causes a problem of model selection to avoid overfitting. One method to solve it is to assume a prior distribution on the full rooted trees. It enables us to avoid overfitting based on the Bayes decision theory. For example, by assigning a low prior probability on a complex model, the MAP estimator prevents the overfitting. Further, we can avoid it by averaging all the models weighted by their posteriors. In this paper, we propose a probability distribution on a set of full rooted trees. Its parametric representation is well suited to calculate the properties of our distribution by recursive functions: the mode, the expectation, the posterior distribution, etc. Although some previous studies have proposed such distributions, they are for specific applications. Therefore, we extract the mathematically essential part of them and derive new generalized methods to calculate the expectation, the posterior distribution, etc.

Theoretical Analysis of the Advantage of Deepening Neural Networks

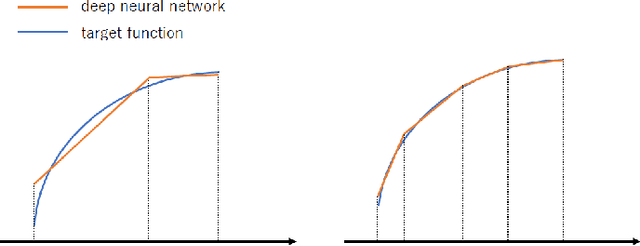
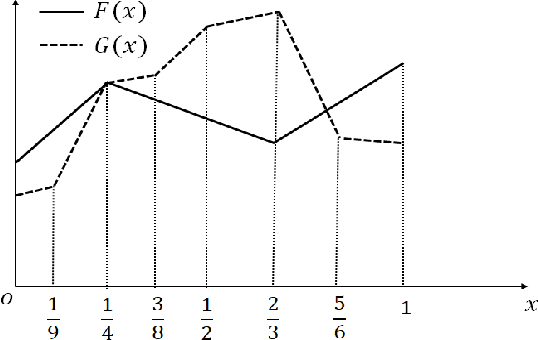
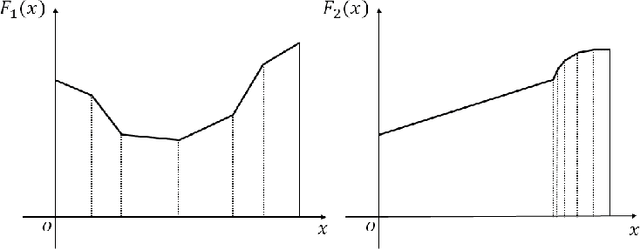
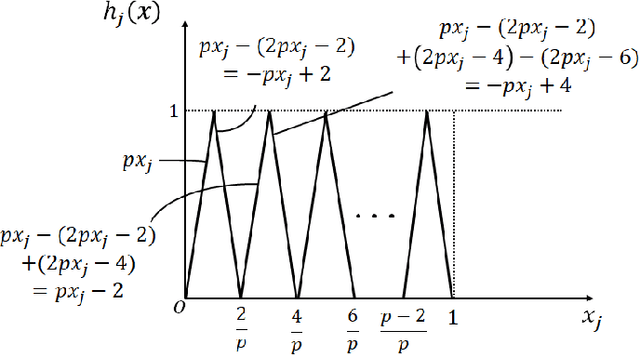
We propose two new criteria to understand the advantage of deepening neural networks. It is important to know the expressivity of functions computable by deep neural networks in order to understand the advantage of deepening neural networks. Unless deep neural networks have enough expressivity, they cannot have good performance even though learning is successful. In this situation, the proposed criteria contribute to understanding the advantage of deepening neural networks since they can evaluate the expressivity independently from the efficiency of learning. The first criterion shows the approximation accuracy of deep neural networks to the target function. This criterion has the background that the goal of deep learning is approximating the target function by deep neural networks. The second criterion shows the property of linear regions of functions computable by deep neural networks. This criterion has the background that deep neural networks whose activation functions are piecewise linear are also piecewise linear. Furthermore, by the two criteria, we show that to increase layers is more effective than to increase units at each layer on improving the expressivity of deep neural networks.