Ryohei Oka
Stochastic 2D Signal Generative Model with Wavelet Packets Basis Regarded as a Random Variable and Bayes Optimal Processing
Jan 26, 2022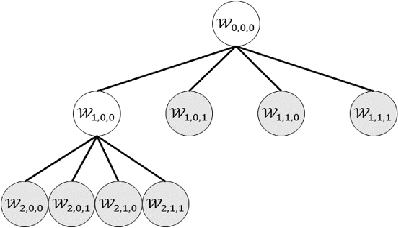
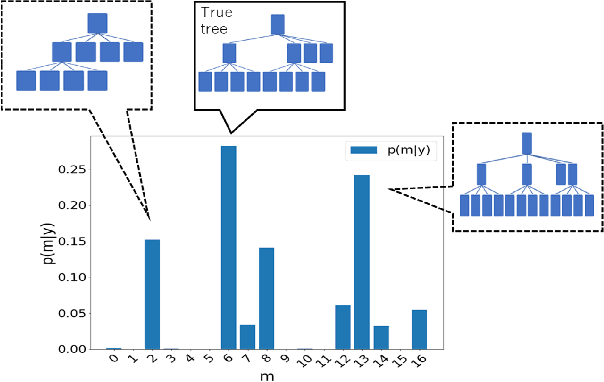
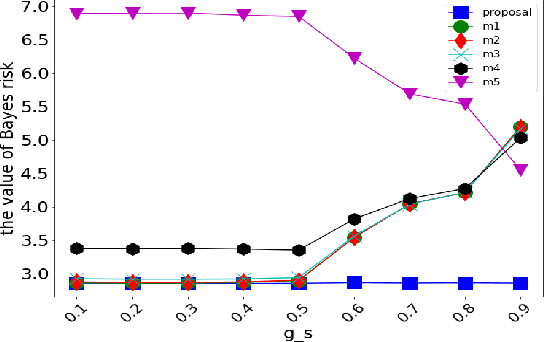
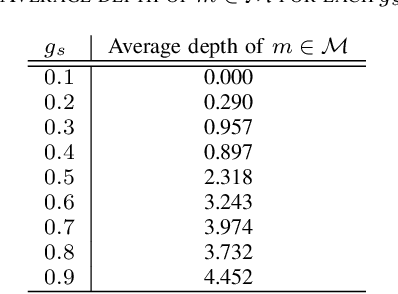
Abstract:This study deals with two-dimensional (2D) signal processing using the wavelet packet transform. When the basis is unknown the candidate of basis increases in exponential order with respect to the signal size. Previous studies do not consider the basis as a random vaiables. Therefore, the cost function needs to be used to select a basis. However, this method is often a heuristic and a greedy search because it is impossible to search all the candidates for a huge number of bases. Therefore, it is difficult to evaluate the entire signal processing under a criterion and also it does not always gurantee the optimality of the entire signal processing. In this study, we propose a stochastic generative model in which the basis is regarded as a random variable. This makes it possible to evaluate entire signal processing under a unified criterion i.e. Bayes criterion. Moreover we can derive an optimal signal processing scheme that achieves the theoretical limit. This derived scheme shows that all the bases should be combined according to the posterior in stead of selecting a single basis. Although exponential order calculations is required for this scheme, we have derived a recursive algorithm for this scheme, which successfully reduces the computational complexity from the exponential order to the polynomial order.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge