Akira Kamatsuka
Probability Distribution on Rooted Trees
Jan 24, 2022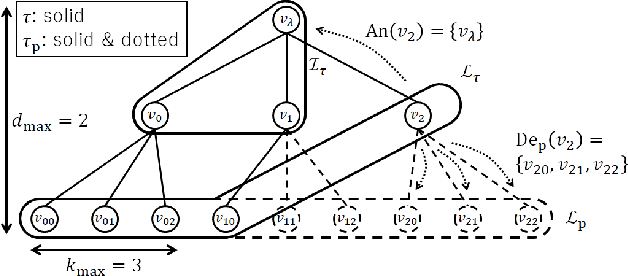
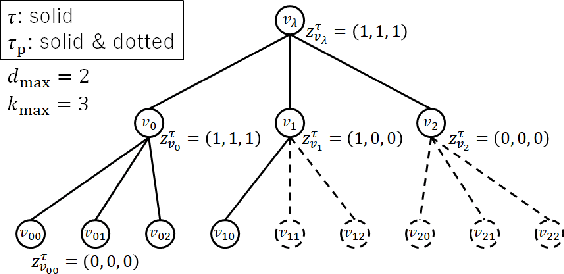
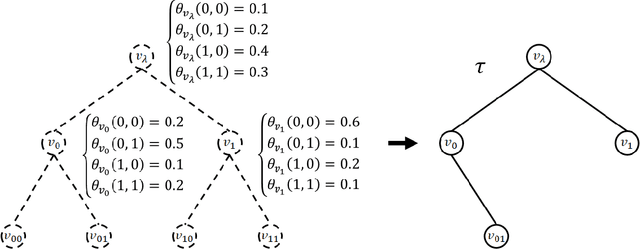
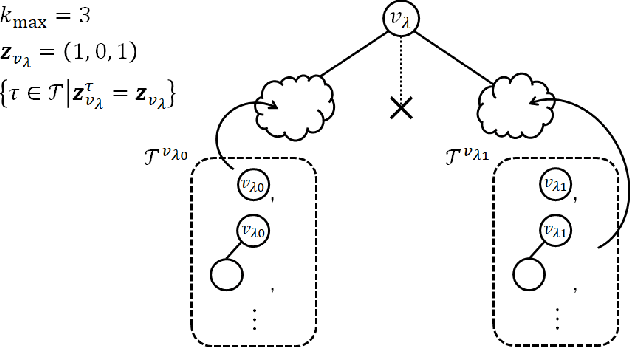
Abstract:The hierarchical and recursive expressive capability of rooted trees is applicable to represent statistical models in various areas, such as data compression, image processing, and machine learning. On the other hand, such hierarchical expressive capability causes a problem in tree selection to avoid overfitting. One unified approach to solve this is a Bayesian approach, on which the rooted tree is regarded as a random variable and a direct loss function can be assumed on the selected model or the predicted value for a new data point. However, all the previous studies on this approach are based on the probability distribution on full trees, to the best of our knowledge. In this paper, we propose a generalized probability distribution for any rooted trees in which only the maximum number of child nodes and the maximum depth are fixed. Furthermore, we derive recursive methods to evaluate the characteristics of the probability distribution without any approximations.
Probability Distribution on Full Rooted Trees
Sep 27, 2021



Abstract:The recursive and hierarchical structure of full rooted trees is used in various areas such as data compression, image processing, and machine learning. In most of these studies, the full rooted tree is not a random variable. It causes a problem of model selection to avoid overfitting. One method to solve it is to assume a prior distribution on the full rooted trees. It enables us to avoid overfitting based on the Bayes decision theory. For example, by assigning a low prior probability on a complex model, the MAP estimator prevents the overfitting. Further, we can avoid it by averaging all the models weighted by their posteriors. In this paper, we propose a probability distribution on a set of full rooted trees. Its parametric representation is well suited to calculate the properties of our distribution by recursive functions: the mode, the expectation, the posterior distribution, etc. Although some previous studies have proposed such distributions, they are for specific applications. Therefore, we extract the mathematically essential part of them and derive new generalized methods to calculate the expectation, the posterior distribution, etc.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge