Zero-Shot Detection of LLM-Generated Code via Approximated Task Conditioning

Detecting Large Language Model (LLM)-generated code is a growing challenge with implications for security, intellectual property, and academic integrity. We investigate the role of conditional probability distributions in improving zero-shot LLM-generated code detection, when considering both the code and the corresponding task prompt that generated it. Our key insight is that when evaluating the probability distribution of code tokens using an LLM, there is little difference between LLM-generated and human-written code. However, conditioning on the task reveals notable differences. This contrasts with natural language text, where differences exist even in the unconditional distributions. Leveraging this, we propose a novel zero-shot detection approach that approximates the original task used to generate a given code snippet and then evaluates token-level entropy under the approximated task conditioning (ATC). We further provide a mathematical intuition, contextualizing our method relative to previous approaches. ATC requires neither access to the generator LLM nor the original task prompts, making it practical for real-world applications. To the best of our knowledge, it achieves state-of-the-art results across benchmarks and generalizes across programming languages, including Python, CPP, and Java. Our findings highlight the importance of task-level conditioning for LLM-generated code detection. The supplementary materials and code are available at https://github.com/maorash/ATC, including the dataset gathering implementation, to foster further research in this area.

Improving the Effective Receptive Field of Message-Passing Neural Networks

Message-Passing Neural Networks (MPNNs) have become a cornerstone for processing and analyzing graph-structured data. However, their effectiveness is often hindered by phenomena such as over-squashing, where long-range dependencies or interactions are inadequately captured and expressed in the MPNN output. This limitation mirrors the challenges of the Effective Receptive Field (ERF) in Convolutional Neural Networks (CNNs), where the theoretical receptive field is underutilized in practice. In this work, we show and theoretically explain the limited ERF problem in MPNNs. Furthermore, inspired by recent advances in ERF augmentation for CNNs, we propose an Interleaved Multiscale Message-Passing Neural Networks (IM-MPNN) architecture to address these problems in MPNNs. Our method incorporates a hierarchical coarsening of the graph, enabling message-passing across multiscale representations and facilitating long-range interactions without excessive depth or parameterization. Through extensive evaluations on benchmarks such as the Long-Range Graph Benchmark (LRGB), we demonstrate substantial improvements over baseline MPNNs in capturing long-range dependencies while maintaining computational efficiency.

Towards Efficient Training of Graph Neural Networks: A Multiscale Approach

Graph Neural Networks (GNNs) have emerged as a powerful tool for learning and inferring from graph-structured data, and are widely used in a variety of applications, often considering large amounts of data and large graphs. However, training on such data requires large memory and extensive computations. In this paper, we introduce a novel framework for efficient multiscale training of GNNs, designed to integrate information across multiscale representations of a graph. Our approach leverages a hierarchical graph representation, taking advantage of coarse graph scales in the training process, where each coarse scale graph has fewer nodes and edges. Based on this approach, we propose a suite of GNN training methods: such as coarse-to-fine, sub-to-full, and multiscale gradient computation. We demonstrate the effectiveness of our methods on various datasets and learning tasks.

Towards Croppable Implicit Neural Representations

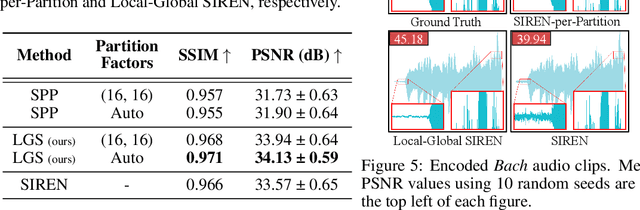
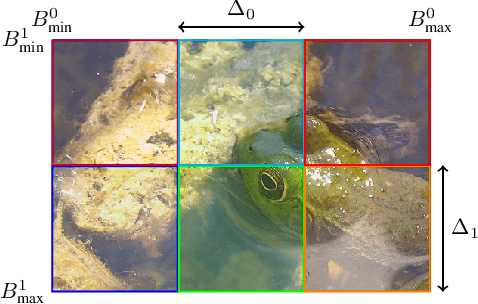
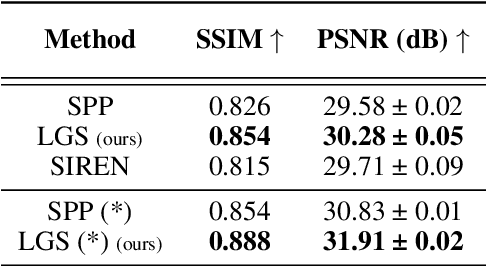
Implicit Neural Representations (INRs) have peaked interest in recent years due to their ability to encode natural signals using neural networks. While INRs allow for useful applications such as interpolating new coordinates and signal compression, their black-box nature makes it difficult to modify them post-training. In this paper we explore the idea of editable INRs, and specifically focus on the widely used cropping operation. To this end, we present Local-Global SIRENs -- a novel INR architecture that supports cropping by design. Local-Global SIRENs are based on combining local and global feature extraction for signal encoding. What makes their design unique is the ability to effortlessly remove specific portions of an encoded signal, with a proportional weight decrease. This is achieved by eliminating the corresponding weights from the network, without the need for retraining. We further show how this architecture can be used to support the straightforward extension of previously encoded signals. Beyond signal editing, we examine how the Local-Global approach can accelerate training, enhance encoding of various signals, improve downstream performance, and be applied to modern INRs such as INCODE, highlighting its potential and flexibility. Code is available at https://github.com/maorash/Local-Global-INRs.

Wavelet Convolutions for Large Receptive Fields

In recent years, there have been attempts to increase the kernel size of Convolutional Neural Nets (CNNs) to mimic the global receptive field of Vision Transformers' (ViTs) self-attention blocks. That approach, however, quickly hit an upper bound and saturated way before achieving a global receptive field. In this work, we demonstrate that by leveraging the Wavelet Transform (WT), it is, in fact, possible to obtain very large receptive fields without suffering from over-parameterization, e.g., for a $k \times k$ receptive field, the number of trainable parameters in the proposed method grows only logarithmically with $k$. The proposed layer, named WTConv, can be used as a drop-in replacement in existing architectures, results in an effective multi-frequency response, and scales gracefully with the size of the receptive field. We demonstrate the effectiveness of the WTConv layer within ConvNeXt and MobileNetV2 architectures for image classification, as well as backbones for downstream tasks, and show it yields additional properties such as robustness to image corruption and an increased response to shapes over textures. Our code is available at https://github.com/BGU-CS-VIL/WTConv.

Global-Local Graph Neural Networks for Node-Classification

The task of graph node classification is often approached by utilizing a local Graph Neural Network (GNN), that learns only local information from the node input features and their adjacency. In this paper, we propose to improve the performance of node classification GNNs by utilizing both global and local information, specifically by learning label- and node- features. We therefore call our method Global-Local-GNN (GLGNN). To learn proper label features, for each label, we maximize the similarity between its features and nodes features that belong to the label, while maximizing the distance between nodes that do not belong to the considered label. We then use the learnt label features to predict the node classification map. We demonstrate our GLGNN using three different GNN backbones, and show that our approach improves baseline performance, revealing the importance of global information utilization for node classification.

Graph Neural Reaction Diffusion Models

The integration of Graph Neural Networks (GNNs) and Neural Ordinary and Partial Differential Equations has been extensively studied in recent years. GNN architectures powered by neural differential equations allow us to reason about their behavior, and develop GNNs with desired properties such as controlled smoothing or energy conservation. In this paper we take inspiration from Turing instabilities in a Reaction Diffusion (RD) system of partial differential equations, and propose a novel family of GNNs based on neural RD systems. We \textcolor{black}{demonstrate} that our RDGNN is powerful for the modeling of various data types, from homophilic, to heterophilic, and spatio-temporal datasets. We discuss the theoretical properties of our RDGNN, its implementation, and show that it improves or offers competitive performance to state-of-the-art methods.

Physics-guided Full Waveform Inversion using Encoder-Solver Convolutional Neural Networks

Full Waveform Inversion (FWI) is an inverse problem for estimating the wave velocity distribution in a given domain, based on observed data on the boundaries. The inversion is computationally demanding because we are required to solve multiple forward problems, either in time or frequency domains, to simulate data that are then iteratively fitted to the observed data. We consider FWI in the frequency domain, where the Helmholtz equation is used as a forward model, and its repeated solution is the main computational bottleneck of the inversion process. To ease this cost, we integrate a learning process of an encoder-solver preconditioner that is based on convolutional neural networks (CNNs). The encoder-solver is trained to effectively precondition the discretized Helmholtz operator given velocity medium parameters. Then, by re-training the CNN between the iterations of the optimization process, the encoder-solver is adapted to the iteratively evolving velocity medium as part of the inversion. Without retraining, the performance of the solver deteriorates as the medium changes. Using our light retraining procedures, we obtain the forward simulations effectively throughout the process. We demonstrate our approach to solving FWI problems using 2D geophysical models with high-frequency data.

An Over Complete Deep Learning Method for Inverse Problems

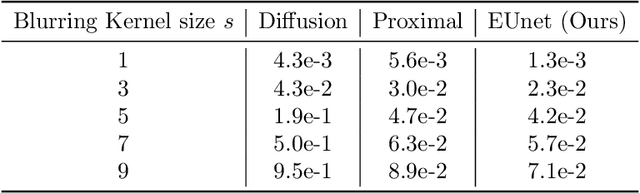
Obtaining meaningful solutions for inverse problems has been a major challenge with many applications in science and engineering. Recent machine learning techniques based on proximal and diffusion-based methods have shown promising results. However, as we show in this work, they can also face challenges when applied to some exemplary problems. We show that similar to previous works on over-complete dictionaries, it is possible to overcome these shortcomings by embedding the solution into higher dimensions. The novelty of the work proposed is that we jointly design and learn the embedding and the regularizer for the embedding vector. We demonstrate the merit of this approach on several exemplary and common inverse problems.

On The Temporal Domain of Differential Equation Inspired Graph Neural Networks

Graph Neural Networks (GNNs) have demonstrated remarkable success in modeling complex relationships in graph-structured data. A recent innovation in this field is the family of Differential Equation-Inspired Graph Neural Networks (DE-GNNs), which leverage principles from continuous dynamical systems to model information flow on graphs with built-in properties such as feature smoothing or preservation. However, existing DE-GNNs rely on first or second-order temporal dependencies. In this paper, we propose a neural extension to those pre-defined temporal dependencies. We show that our model, called TDE-GNN, can capture a wide range of temporal dynamics that go beyond typical first or second-order methods, and provide use cases where existing temporal models are challenged. We demonstrate the benefit of learning the temporal dependencies using our method rather than using pre-defined temporal dynamics on several graph benchmarks.