An Over Complete Deep Learning Method for Inverse Problems
Paper and Code
Feb 07, 2024

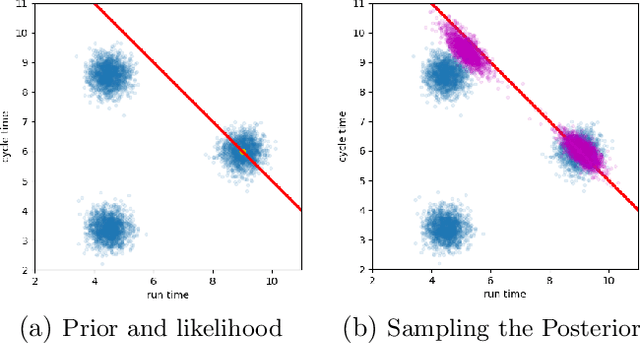
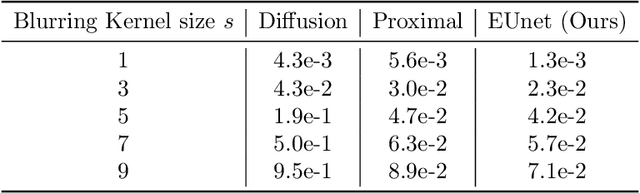
Obtaining meaningful solutions for inverse problems has been a major challenge with many applications in science and engineering. Recent machine learning techniques based on proximal and diffusion-based methods have shown promising results. However, as we show in this work, they can also face challenges when applied to some exemplary problems. We show that similar to previous works on over-complete dictionaries, it is possible to overcome these shortcomings by embedding the solution into higher dimensions. The novelty of the work proposed is that we jointly design and learn the embedding and the regularizer for the embedding vector. We demonstrate the merit of this approach on several exemplary and common inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge