A Geometric Unification of Generative AI with Manifold-Probabilistic Projection Models

The foundational premise of generative AI for images is the assumption that images are inherently low-dimensional objects embedded within a high-dimensional space. Additionally, it is often implicitly assumed that thematic image datasets form smooth or piecewise smooth manifolds. Common approaches overlook the geometric structure and focus solely on probabilistic methods, approximating the probability distribution through universal approximation techniques such as the kernel method. In some generative models, the low dimensional nature of the data manifest itself by the introduction of a lower dimensional latent space. Yet, the probability distribution in the latent or the manifold coordinate space is considered uninteresting and is predefined or considered uniform. This study unifies the geometric and probabilistic perspectives by providing a geometric framework and a kernel-based probabilistic method simultaneously. The resulting framework demystifies diffusion models by interpreting them as a projection mechanism onto the manifold of ``good images''. This interpretation leads to the construction of a new deterministic model, the Manifold-Probabilistic Projection Model (MPPM), which operates in both the representation (pixel) space and the latent space. We demonstrate that the Latent MPPM (LMPPM) outperforms the Latent Diffusion Model (LDM) across various datasets, achieving superior results in terms of image restoration and generation.

Active Learning via Classifier Impact and Greedy Selection for Interactive Image Retrieval

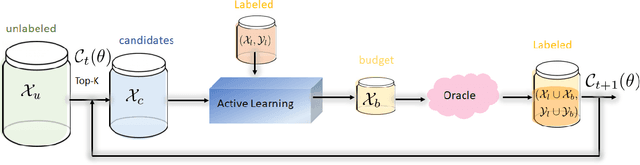
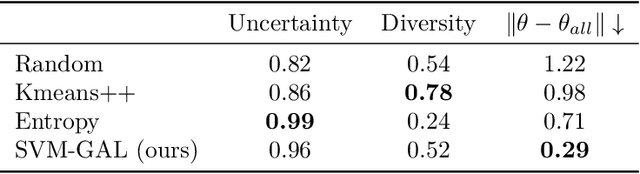
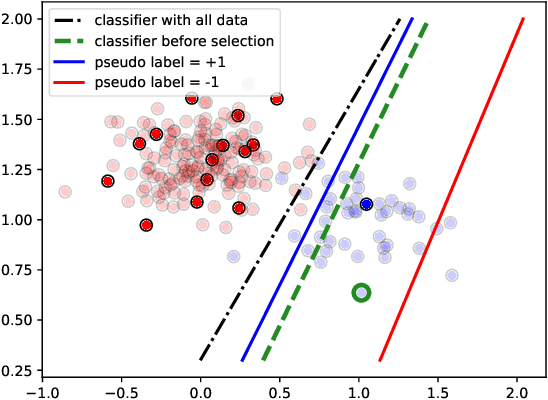
Active Learning (AL) is a user-interactive approach aimed at reducing annotation costs by selecting the most crucial examples to label. Although AL has been extensively studied for image classification tasks, the specific scenario of interactive image retrieval has received relatively little attention. This scenario presents unique characteristics, including an open-set and class-imbalanced binary classification, starting with very few labeled samples. We introduce a novel batch-mode Active Learning framework named GAL (Greedy Active Learning) that better copes with this application. It incorporates a new acquisition function for sample selection that measures the impact of each unlabeled sample on the classifier. We further embed this strategy in a greedy selection approach, better exploiting the samples within each batch. We evaluate our framework with both linear (SVM) and non-linear MLP/Gaussian Process classifiers. For the Gaussian Process case, we show a theoretical guarantee on the greedy approximation. Finally, we assess our performance for the interactive content-based image retrieval task on several benchmarks and demonstrate its superiority over existing approaches and common baselines. Code is available at https://github.com/barleah/GreedyAL.

Solving the functional Eigen-Problem using Neural Networks

In this work, we explore the ability of NN (Neural Networks) to serve as a tool for finding eigen-pairs of ordinary differential equations. The question we aime to address is whether, given a self-adjoint operator, we can learn what are the eigenfunctions, and their matching eigenvalues. The topic of solving the eigen-problem is widely discussed in Image Processing, as many image processing algorithms can be thought of as such operators. We suggest an alternative to numeric methods of finding eigenpairs, which may potentially be more robust and have the ability to solve more complex problems. In this work, we focus on simple problems for which the analytical solution is known. This way, we are able to make initial steps in discovering the capabilities and shortcomings of DNN (Deep Neural Networks) in the given setting.

Unsupervised Deep Learning Algorithm for PDE-based Forward and Inverse Problems

We propose a neural network-based algorithm for solving forward and inverse problems for partial differential equations in unsupervised fashion. The solution is approximated by a deep neural network which is the minimizer of a cost function, and satisfies the PDE, boundary conditions, and additional regularizations. The method is mesh free and can be easily applied to an arbitrary regular domain. We focus on 2D second order elliptical system with non-constant coefficients, with application to Electrical Impedance Tomography.