Scaling Neural Tangent Kernels via Sketching and Random Features

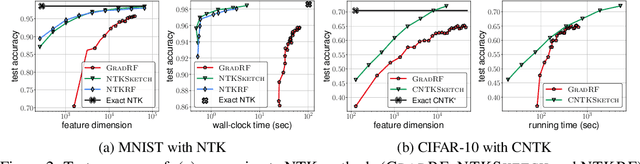
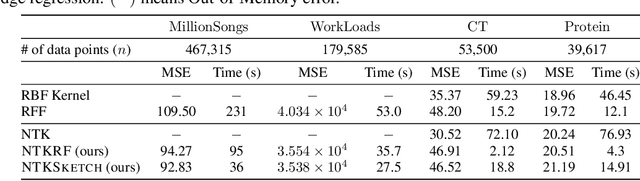
The Neural Tangent Kernel (NTK) characterizes the behavior of infinitely-wide neural networks trained under least squares loss by gradient descent. Recent works also report that NTK regression can outperform finitely-wide neural networks trained on small-scale datasets. However, the computational complexity of kernel methods has limited its use in large-scale learning tasks. To accelerate learning with NTK, we design a near input-sparsity time approximation algorithm for NTK, by sketching the polynomial expansions of arc-cosine kernels: our sketch for the convolutional counterpart of NTK (CNTK) can transform any image using a linear runtime in the number of pixels. Furthermore, we prove a spectral approximation guarantee for the NTK matrix, by combining random features (based on leverage score sampling) of the arc-cosine kernels with a sketching algorithm. We benchmark our methods on various large-scale regression and classification tasks and show that a linear regressor trained on our CNTK features matches the accuracy of exact CNTK on CIFAR-10 dataset while achieving 150x speedup.

An Exploration into why Output Regularization Mitigates Label Noise

Label noise presents a real challenge for supervised learning algorithms. Consequently, mitigating label noise has attracted immense research in recent years. Noise robust losses is one of the more promising approaches for dealing with label noise, as these methods only require changing the loss function and do not require changing the design of the classifier itself, which can be expensive in terms of development time. In this work we focus on losses that use output regularization (such as label smoothing and entropy). Although these losses perform well in practice, their ability to mitigate label noise lack mathematical rigor. In this work we aim at closing this gap by showing that losses, which incorporate an output regularization term, become symmetric as the regularization coefficient goes to infinity. We argue that the regularization coefficient can be seen as a hyper-parameter controlling the symmetricity, and thus, the noise robustness of the loss function.

Random Features for the Neural Tangent Kernel

The Neural Tangent Kernel (NTK) has discovered connections between deep neural networks and kernel methods with insights of optimization and generalization. Motivated by this, recent works report that NTK can achieve better performances compared to training neural networks on small-scale datasets. However, results under large-scale settings are hardly studied due to the computational limitation of kernel methods. In this work, we propose an efficient feature map construction of the NTK of fully-connected ReLU network which enables us to apply it to large-scale datasets. We combine random features of the arc-cosine kernels with a sketching-based algorithm which can run in linear with respect to both the number of data points and input dimension. We show that dimension of the resulting features is much smaller than other baseline feature map constructions to achieve comparable error bounds both in theory and practice. We additionally utilize the leverage score based sampling for improved bounds of arc-cosine random features and prove a spectral approximation guarantee of the proposed feature map to the NTK matrix of two-layer neural network. We benchmark a variety of machine learning tasks to demonstrate the superiority of the proposed scheme. In particular, our algorithm can run tens of magnitude faster than the exact kernel methods for large-scale settings without performance loss.

Experimental Design for Overparameterized Learning with Application to Single Shot Deep Active Learning

The impressive performance exhibited by modern machine learning models hinges on the ability to train such models on a very large amounts of labeled data. However, since access to large volumes of labeled data is often limited or expensive, it is desirable to alleviate this bottleneck by carefully curating the training set. Optimal experimental design is a well-established paradigm for selecting data point to be labeled so to maximally inform the learning process. Unfortunately, classical theory on optimal experimental design focuses on selecting examples in order to learn underparameterized (and thus, non-interpolative) models, while modern machine learning models such as deep neural networks are overparameterized, and oftentimes are trained to be interpolative. As such, classical experimental design methods are not applicable in many modern learning setups. Indeed, the predictive performance of underparameterized models tends to be variance dominated, so classical experimental design focuses on variance reduction, while the predictive performance of overparameterized models can also be, as is shown in this paper, bias dominated or of mixed nature. In this paper we propose a design strategy that is well suited for overparameterized regression and interpolation, and we demonstrate the applicability of our method in the context of deep learning by proposing a new algorithm for single-shot deep active learning.

Overcoming Forgetting in Federated Learning on Non-IID Data

We tackle the problem of Federated Learning in the non i.i.d. case, in which local models drift apart, inhibiting learning. Building on an analogy with Lifelong Learning, we adapt a solution for catastrophic forgetting to Federated Learning. We add a penalty term to the loss function, compelling all local models to converge to a shared optimum. We show that this can be done efficiently for communication (adding no further privacy risks), scaling with the number of nodes in the distributed setting. Our experiments show that this method is superior to competing ones for image recognition on the MNIST dataset.