AlphaEvolve: A coding agent for scientific and algorithmic discovery

In this white paper, we present AlphaEvolve, an evolutionary coding agent that substantially enhances capabilities of state-of-the-art LLMs on highly challenging tasks such as tackling open scientific problems or optimizing critical pieces of computational infrastructure. AlphaEvolve orchestrates an autonomous pipeline of LLMs, whose task is to improve an algorithm by making direct changes to the code. Using an evolutionary approach, continuously receiving feedback from one or more evaluators, AlphaEvolve iteratively improves the algorithm, potentially leading to new scientific and practical discoveries. We demonstrate the broad applicability of this approach by applying it to a number of important computational problems. When applied to optimizing critical components of large-scale computational stacks at Google, AlphaEvolve developed a more efficient scheduling algorithm for data centers, found a functionally equivalent simplification in the circuit design of hardware accelerators, and accelerated the training of the LLM underpinning AlphaEvolve itself. Furthermore, AlphaEvolve discovered novel, provably correct algorithms that surpass state-of-the-art solutions on a spectrum of problems in mathematics and computer science, significantly expanding the scope of prior automated discovery methods (Romera-Paredes et al., 2023). Notably, AlphaEvolve developed a search algorithm that found a procedure to multiply two $4 \times 4$ complex-valued matrices using $48$ scalar multiplications; offering the first improvement, after 56 years, over Strassen's algorithm in this setting. We believe AlphaEvolve and coding agents like it can have a significant impact in improving solutions of problems across many areas of science and computation.

Good, Cheap, and Fast: Overfitted Image Compression with Wasserstein Distortion

Inspired by the success of generative image models, recent work on learned image compression increasingly focuses on better probabilistic models of the natural image distribution, leading to excellent image quality. This, however, comes at the expense of a computational complexity that is several orders of magnitude higher than today's commercial codecs, and thus prohibitive for most practical applications. With this paper, we demonstrate that by focusing on modeling visual perception rather than the data distribution, we can achieve a very good trade-off between visual quality and bit rate similar to "generative" compression models such as HiFiC, while requiring less than 1% of the multiply-accumulate operations (MACs) for decompression. We do this by optimizing C3, an overfitted image codec, for Wasserstein Distortion (WD), and evaluating the image reconstructions with a human rater study. The study also reveals that WD outperforms other perceptual quality metrics such as LPIPS, DISTS, and MS-SSIM, both as an optimization objective and as a predictor of human ratings, achieving over 94% Pearson correlation with Elo scores.

C3: High-performance and low-complexity neural compression from a single image or video

Most neural compression models are trained on large datasets of images or videos in order to generalize to unseen data. Such generalization typically requires large and expressive architectures with a high decoding complexity. Here we introduce C3, a neural compression method with strong rate-distortion (RD) performance that instead overfits a small model to each image or video separately. The resulting decoding complexity of C3 can be an order of magnitude lower than neural baselines with similar RD performance. C3 builds on COOL-CHIC (Ladune et al.) and makes several simple and effective improvements for images. We further develop new methodology to apply C3 to videos. On the CLIC2020 image benchmark, we match the RD performance of VTM, the reference implementation of the H.266 codec, with less than 3k MACs/pixel for decoding. On the UVG video benchmark, we match the RD performance of the Video Compression Transformer (Mentzer et al.), a well-established neural video codec, with less than 5k MACs/pixel for decoding.

Deep Stochastic Processes via Functional Markov Transition Operators

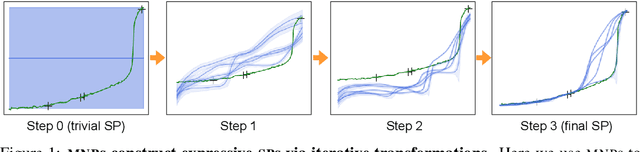
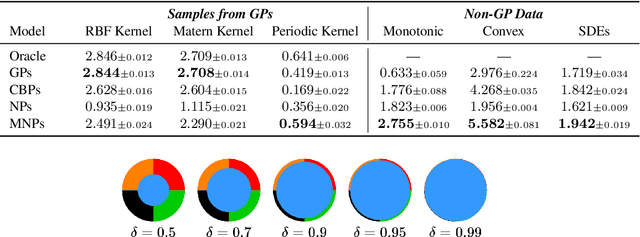
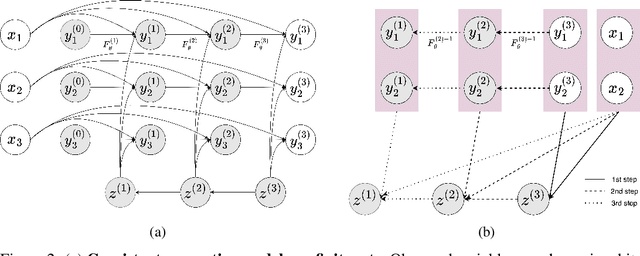
We introduce Markov Neural Processes (MNPs), a new class of Stochastic Processes (SPs) which are constructed by stacking sequences of neural parameterised Markov transition operators in function space. We prove that these Markov transition operators can preserve the exchangeability and consistency of SPs. Therefore, the proposed iterative construction adds substantial flexibility and expressivity to the original framework of Neural Processes (NPs) without compromising consistency or adding restrictions. Our experiments demonstrate clear advantages of MNPs over baseline models on a variety of tasks.

Spatial Functa: Scaling Functa to ImageNet Classification and Generation

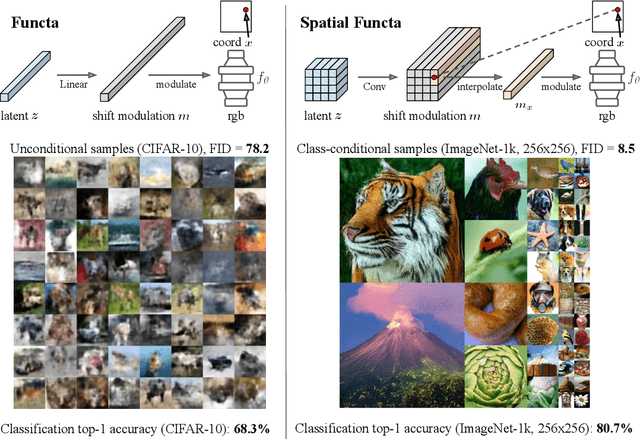
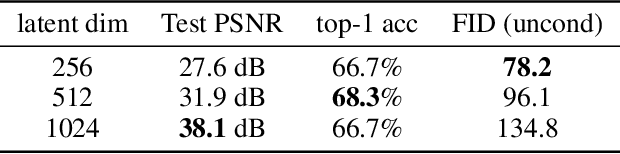
Neural fields, also known as implicit neural representations, have emerged as a powerful means to represent complex signals of various modalities. Based on this Dupont et al. (2022) introduce a framework that views neural fields as data, termed *functa*, and proposes to do deep learning directly on this dataset of neural fields. In this work, we show that the proposed framework faces limitations when scaling up to even moderately complex datasets such as CIFAR-10. We then propose *spatial functa*, which overcome these limitations by using spatially arranged latent representations of neural fields, thereby allowing us to scale up the approach to ImageNet-1k at 256x256 resolution. We demonstrate competitive performance to Vision Transformers (Steiner et al., 2022) on classification and Latent Diffusion (Rombach et al., 2022) on image generation respectively.

COIN++: Data Agnostic Neural Compression

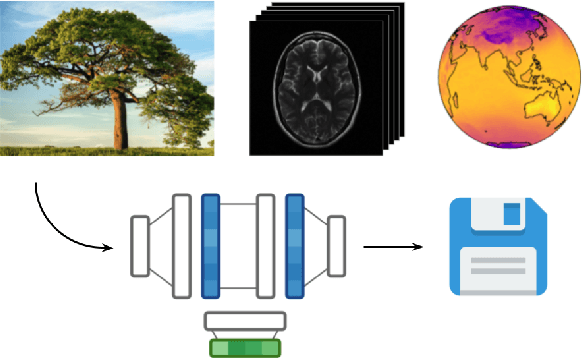
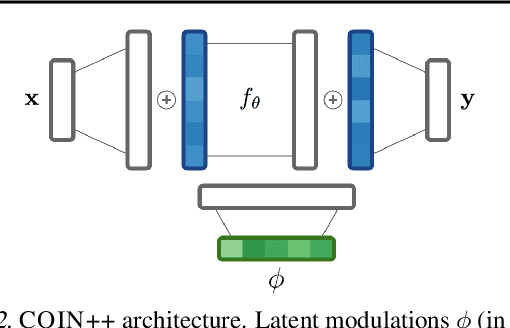
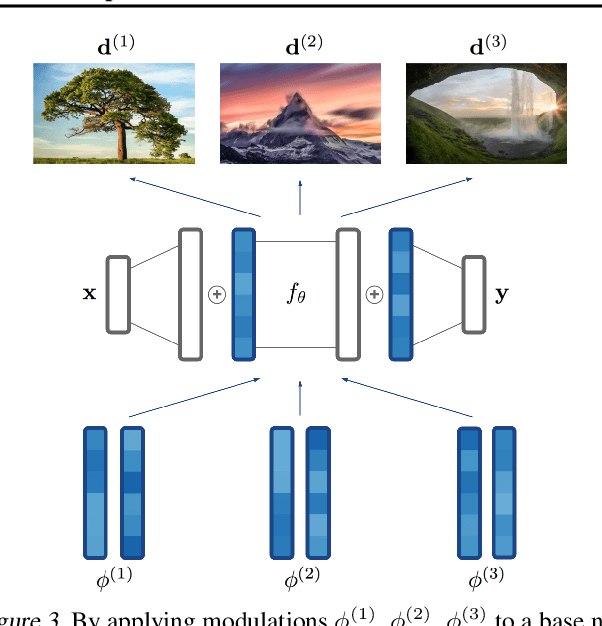
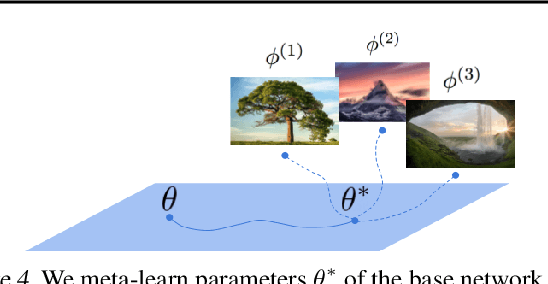
Neural compression algorithms are typically based on autoencoders that require specialized encoder and decoder architectures for different data modalities. In this paper, we propose COIN++, a neural compression framework that seamlessly handles a wide range of data modalities. Our approach is based on converting data to implicit neural representations, i.e. neural functions that map coordinates (such as pixel locations) to features (such as RGB values). Then, instead of storing the weights of the implicit neural representation directly, we store modulations applied to a meta-learned base network as a compressed code for the data. We further quantize and entropy code these modulations, leading to large compression gains while reducing encoding time by two orders of magnitude compared to baselines. We empirically demonstrate the effectiveness of our method by compressing various data modalities, from images to medical and climate data.

From data to functa: Your data point is a function and you should treat it like one

It is common practice in deep learning to represent a measurement of the world on a discrete grid, e.g. a 2D grid of pixels. However, the underlying signal represented by these measurements is often continuous, e.g. the scene depicted in an image. A powerful continuous alternative is then to represent these measurements using an implicit neural representation, a neural function trained to output the appropriate measurement value for any input spatial location. In this paper, we take this idea to its next level: what would it take to perform deep learning on these functions instead, treating them as data? In this context we refer to the data as functa, and propose a framework for deep learning on functa. This view presents a number of challenges around efficient conversion from data to functa, compact representation of functa, and effectively solving downstream tasks on functa. We outline a recipe to overcome these challenges and apply it to a wide range of data modalities including images, 3D shapes, neural radiance fields (NeRF) and data on manifolds. We demonstrate that this approach has various compelling properties across data modalities, in particular on the canonical tasks of generative modeling, data imputation, novel view synthesis and classification.

COIN: COmpression with Implicit Neural representations

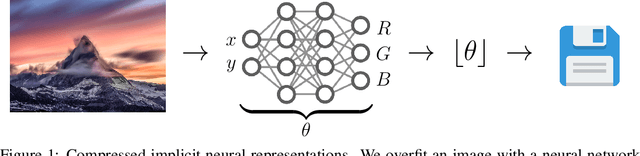
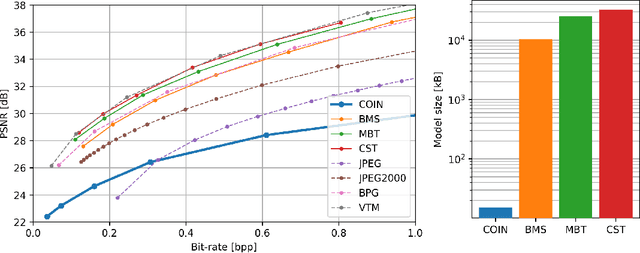
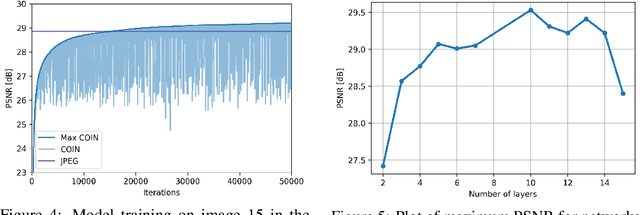
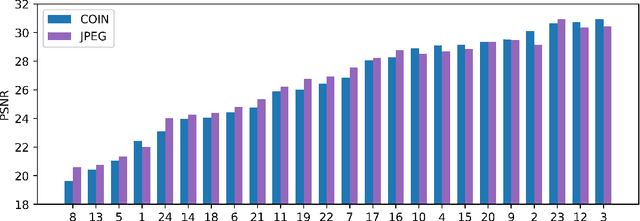
We propose a new simple approach for image compression: instead of storing the RGB values for each pixel of an image, we store the weights of a neural network overfitted to the image. Specifically, to encode an image, we fit it with an MLP which maps pixel locations to RGB values. We then quantize and store the weights of this MLP as a code for the image. To decode the image, we simply evaluate the MLP at every pixel location. We found that this simple approach outperforms JPEG at low bit-rates, even without entropy coding or learning a distribution over weights. While our framework is not yet competitive with state of the art compression methods, we show that it has various attractive properties which could make it a viable alternative to other neural data compression approaches.

Generative Models as Distributions of Functions

Generative models are typically trained on grid-like data such as images. As a result, the size of these models usually scales directly with the underlying grid resolution. In this paper, we abandon discretized grids and instead parameterize individual data points by continuous functions. We then build generative models by learning distributions over such functions. By treating data points as functions, we can abstract away from the specific type of data we train on and construct models that scale independently of signal resolution and dimension. To train our model, we use an adversarial approach with a discriminator that acts directly on continuous signals. Through experiments on both images and 3D shapes, we demonstrate that our model can learn rich distributions of functions independently of data type and resolution.

LieTransformer: Equivariant self-attention for Lie Groups

Group equivariant neural networks are used as building blocks of group invariant neural networks, which have been shown to improve generalisation performance and data efficiency through principled parameter sharing. Such works have mostly focused on group equivariant convolutions, building on the result that group equivariant linear maps are necessarily convolutions. In this work, we extend the scope of the literature to non-linear neural network modules, namely self-attention, that is emerging as a prominent building block of deep learning models. We propose the LieTransformer, an architecture composed of LieSelfAttention layers that are equivariant to arbitrary Lie groups and their discrete subgroups. We demonstrate the generality of our approach by showing experimental results that are competitive to baseline methods on a wide range of tasks: shape counting on point clouds, molecular property regression and modelling particle trajectories under Hamiltonian dynamics.