Disentangling shared and private latent factors in multimodal Variational Autoencoders

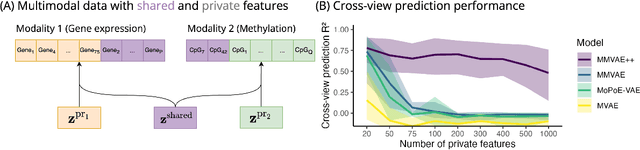
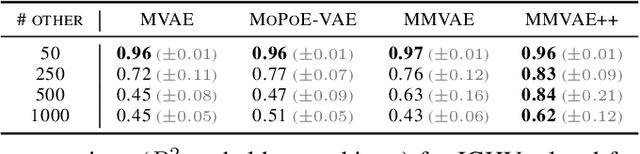
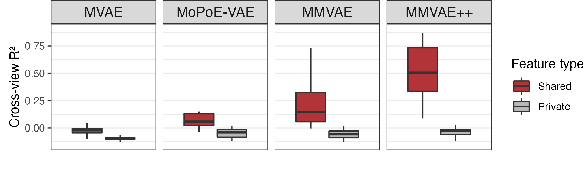
Generative models for multimodal data permit the identification of latent factors that may be associated with important determinants of observed data heterogeneity. Common or shared factors could be important for explaining variation across modalities whereas other factors may be private and important only for the explanation of a single modality. Multimodal Variational Autoencoders, such as MVAE and MMVAE, are a natural choice for inferring those underlying latent factors and separating shared variation from private. In this work, we investigate their capability to reliably perform this disentanglement. In particular, we highlight a challenging problem setting where modality-specific variation dominates the shared signal. Taking a cross-modal prediction perspective, we demonstrate limitations of existing models, and propose a modification how to make them more robust to modality-specific variation. Our findings are supported by experiments on synthetic as well as various real-world multi-omics data sets.

Deep Stochastic Processes via Functional Markov Transition Operators

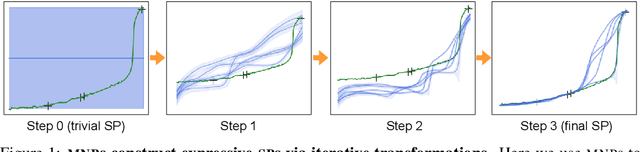
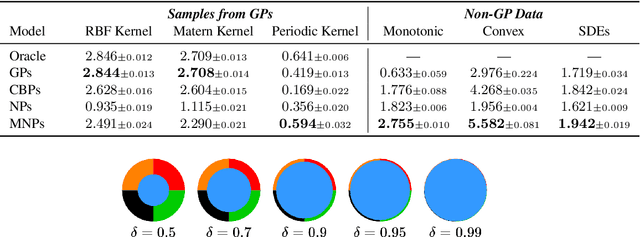
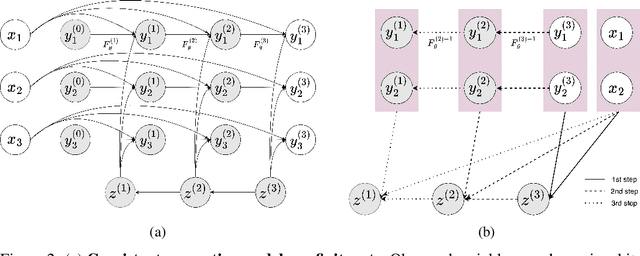
We introduce Markov Neural Processes (MNPs), a new class of Stochastic Processes (SPs) which are constructed by stacking sequences of neural parameterised Markov transition operators in function space. We prove that these Markov transition operators can preserve the exchangeability and consistency of SPs. Therefore, the proposed iterative construction adds substantial flexibility and expressivity to the original framework of Neural Processes (NPs) without compromising consistency or adding restrictions. Our experiments demonstrate clear advantages of MNPs over baseline models on a variety of tasks.

Neural Decomposition: Functional ANOVA with Variational Autoencoders

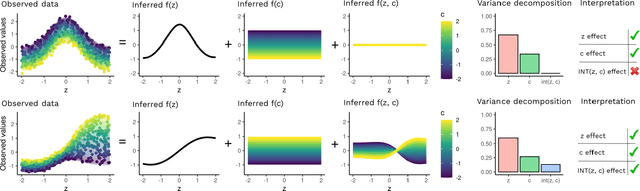
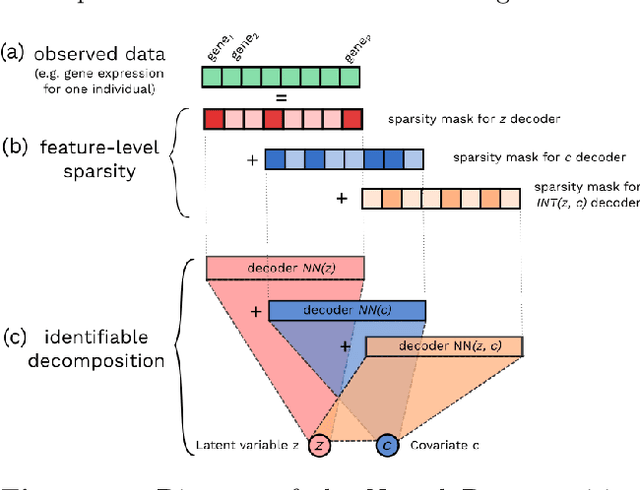
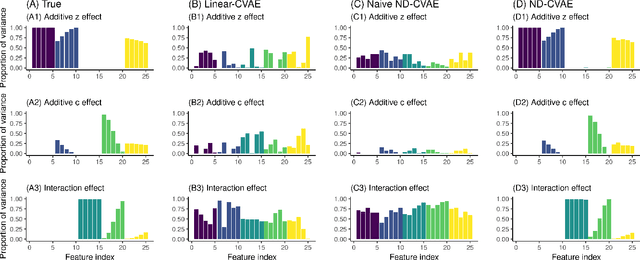
Variational Autoencoders (VAEs) have become a popular approach for dimensionality reduction. However, despite their ability to identify latent low-dimensional structures embedded within high-dimensional data, these latent representations are typically hard to interpret on their own. Due to the black-box nature of VAEs, their utility for healthcare and genomics applications has been limited. In this paper, we focus on characterising the sources of variation in Conditional VAEs. Our goal is to provide a feature-level variance decomposition, i.e. to decompose variation in the data by separating out the marginal additive effects of latent variables z and fixed inputs c from their non-linear interactions. We propose to achieve this through what we call Neural Decomposition - an adaptation of the well-known concept of functional ANOVA variance decomposition from classical statistics to deep learning models. We show how identifiability can be achieved by training models subject to constraints on the marginal properties of the decoder networks. We demonstrate the utility of our Neural Decomposition on a series of synthetic examples as well as high-dimensional genomics data.

BasisVAE: Translation-invariant feature-level clustering with Variational Autoencoders

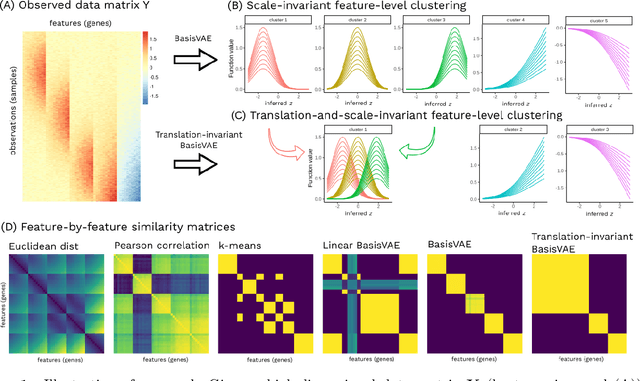
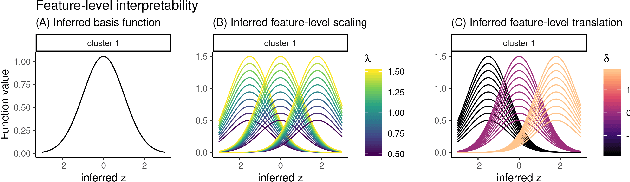
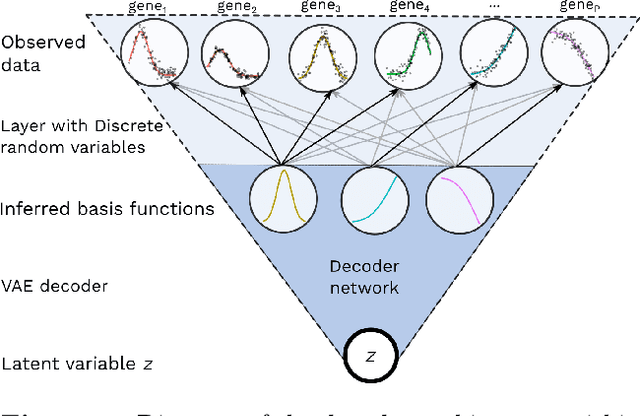
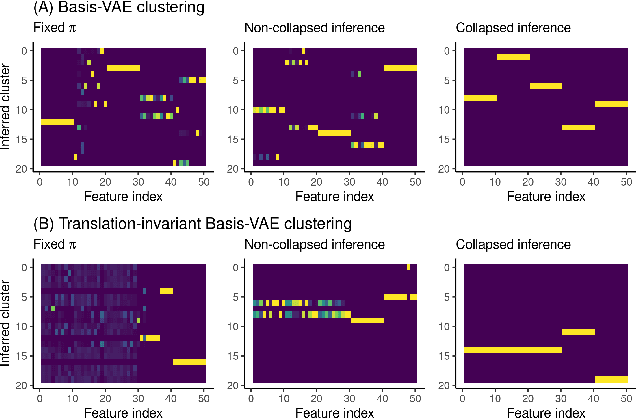
Variational Autoencoders (VAEs) provide a flexible and scalable framework for non-linear dimensionality reduction. However, in application domains such as genomics where data sets are typically tabular and high-dimensional, a black-box approach to dimensionality reduction does not provide sufficient insights. Common data analysis workflows additionally use clustering techniques to identify groups of similar features. This usually leads to a two-stage process, however, it would be desirable to construct a joint modelling framework for simultaneous dimensionality reduction and clustering of features. In this paper, we propose to achieve this through the BasisVAE: a combination of the VAE and a probabilistic clustering prior, which lets us learn a one-hot basis function representation as part of the decoder network. Furthermore, for scenarios where not all features are aligned, we develop an extension to handle translation-invariant basis functions. We show how a collapsed variational inference scheme leads to scalable and efficient inference for BasisVAE, demonstrated on various toy examples as well as on single-cell gene expression data.

Covariate Gaussian Process Latent Variable Models

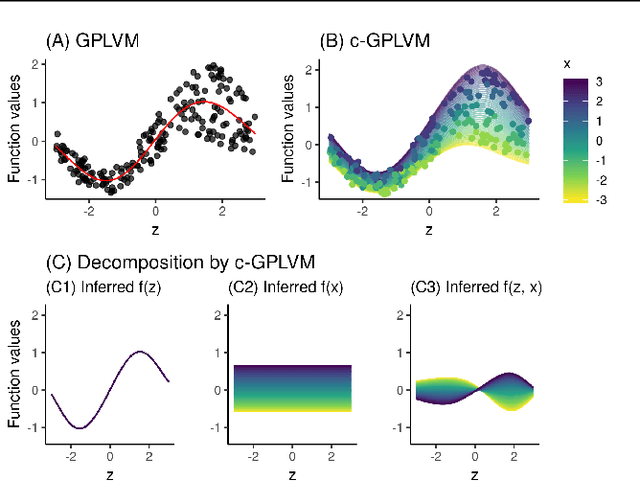
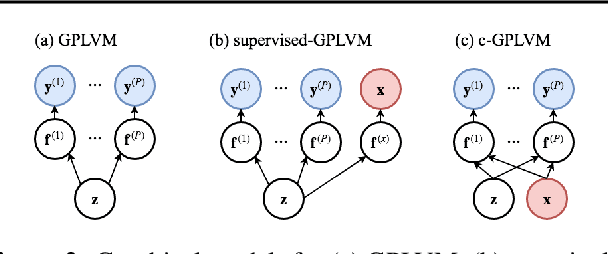
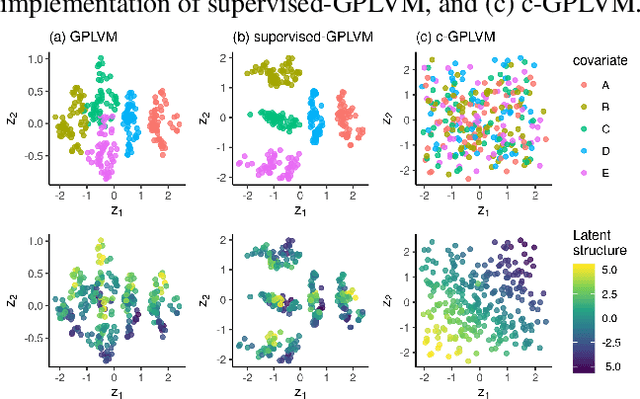
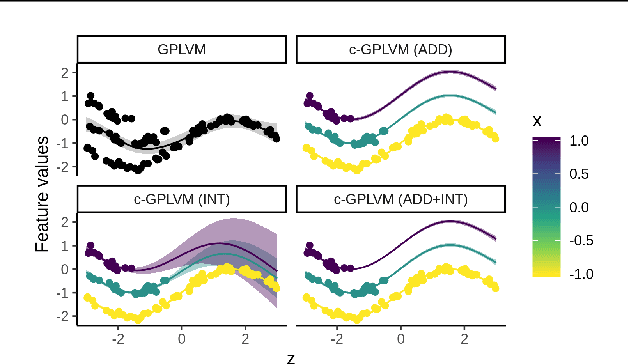
Gaussian Process Regression (GPR) and Gaussian Process Latent Variable Models (GPLVM) offer a principled way of performing probabilistic non-linear regression and dimensionality reduction. In this paper we propose a hybrid between the two, the covariate-GPLVM (c-GPLVM), to perform dimensionality reduction in the presence of covariate information (e.g. continuous covariates, class labels, or censored survival times). This construction lets us adjust for covariate effects and reveals meaningful latent structure which is not revealed when using GPLVM. Furthermore, we introduce structured decomposable kernels which will let us interpret how the fixed and latent inputs contribute to feature-level variation, e.g. identify the presence of a non-linear interaction. We demonstrate the utility of this model on applications in disease progression modelling from high-dimensional gene expression data in the presence of additional phenotypes.

Rejection-free Ensemble MCMC with applications to Factorial Hidden Markov Models

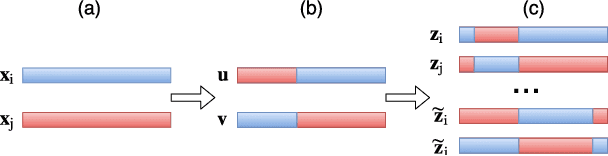
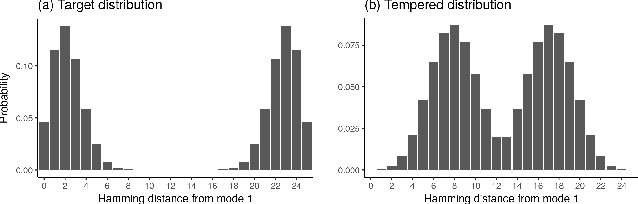
Bayesian inference for complex models is challenging due to the need to explore high-dimensional spaces and multimodality and standard Monte Carlo samplers can have difficulties effectively exploring the posterior. We introduce a general purpose rejection-free ensemble Markov Chain Monte Carlo (MCMC) technique to improve on existing poorly mixing samplers. This is achieved by combining parallel tempering and an auxiliary variable move to exchange information between the chains. We demonstrate this ensemble MCMC scheme on Bayesian inference in Factorial Hidden Markov Models. This high-dimensional inference problem is difficult due to the exponentially sized latent variable space. Existing sampling approaches mix slowly and can get trapped in local modes. We show that the performance of these samplers is improved by our rejection-free ensemble technique and that the method is attractive and "easy-to-use" since no parameter tuning is required.