Covariate Gaussian Process Latent Variable Models

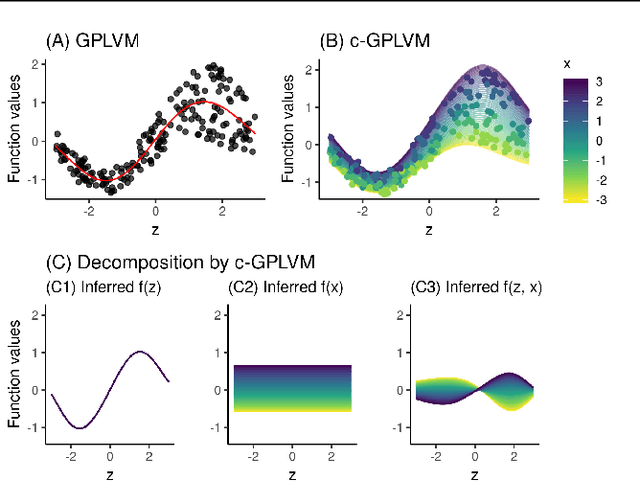
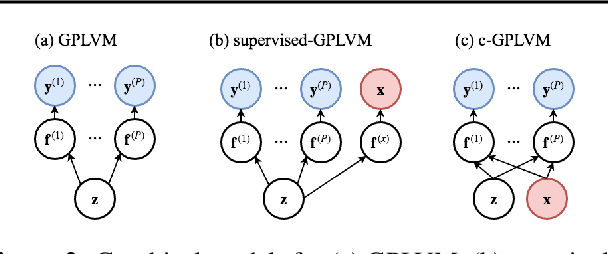
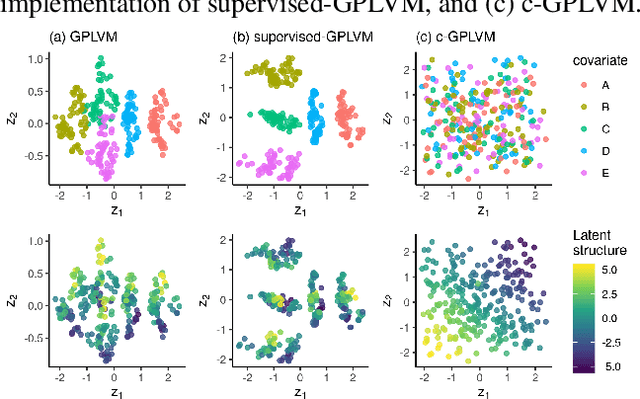
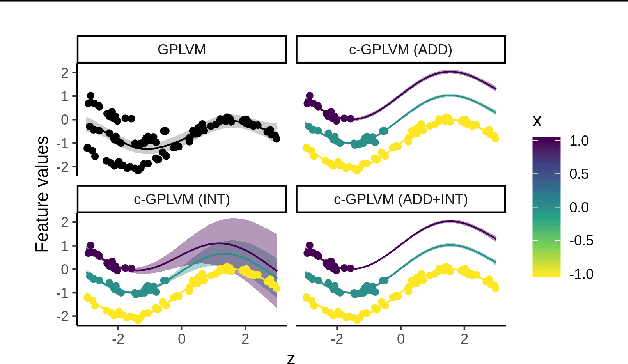
Gaussian Process Regression (GPR) and Gaussian Process Latent Variable Models (GPLVM) offer a principled way of performing probabilistic non-linear regression and dimensionality reduction. In this paper we propose a hybrid between the two, the covariate-GPLVM (c-GPLVM), to perform dimensionality reduction in the presence of covariate information (e.g. continuous covariates, class labels, or censored survival times). This construction lets us adjust for covariate effects and reveals meaningful latent structure which is not revealed when using GPLVM. Furthermore, we introduce structured decomposable kernels which will let us interpret how the fixed and latent inputs contribute to feature-level variation, e.g. identify the presence of a non-linear interaction. We demonstrate the utility of this model on applications in disease progression modelling from high-dimensional gene expression data in the presence of additional phenotypes.