Covariate Gaussian Process Latent Variable Models

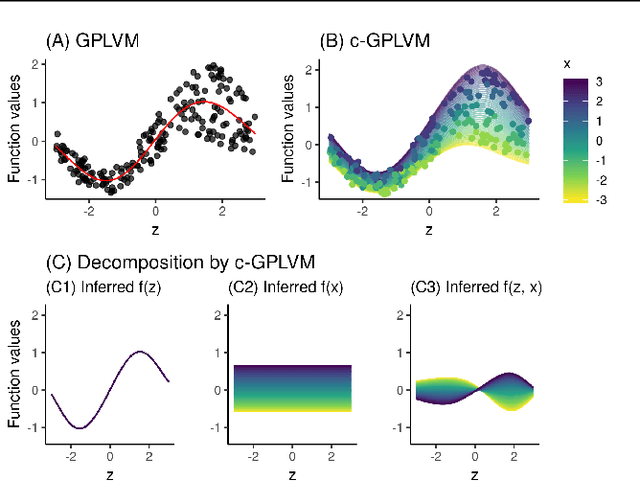
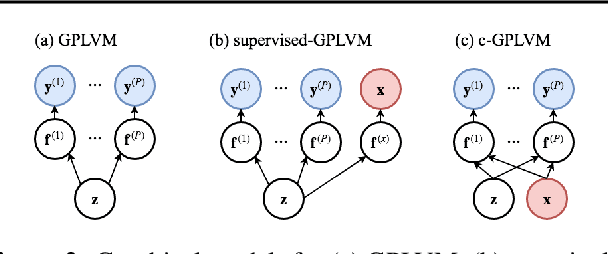
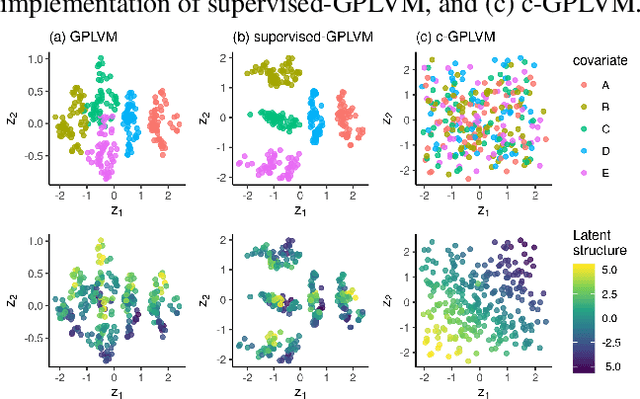
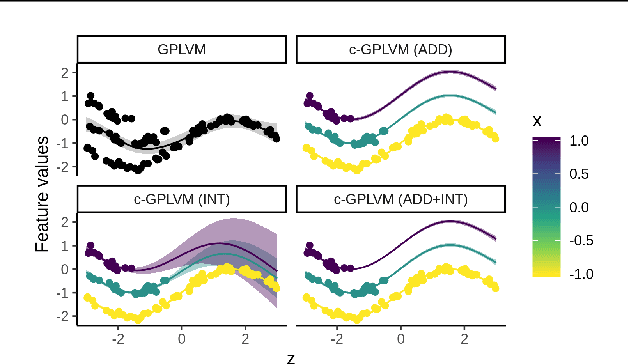
Gaussian Process Regression (GPR) and Gaussian Process Latent Variable Models (GPLVM) offer a principled way of performing probabilistic non-linear regression and dimensionality reduction. In this paper we propose a hybrid between the two, the covariate-GPLVM (c-GPLVM), to perform dimensionality reduction in the presence of covariate information (e.g. continuous covariates, class labels, or censored survival times). This construction lets us adjust for covariate effects and reveals meaningful latent structure which is not revealed when using GPLVM. Furthermore, we introduce structured decomposable kernels which will let us interpret how the fixed and latent inputs contribute to feature-level variation, e.g. identify the presence of a non-linear interaction. We demonstrate the utility of this model on applications in disease progression modelling from high-dimensional gene expression data in the presence of additional phenotypes.

Stratification of patient trajectories using covariate latent variable models

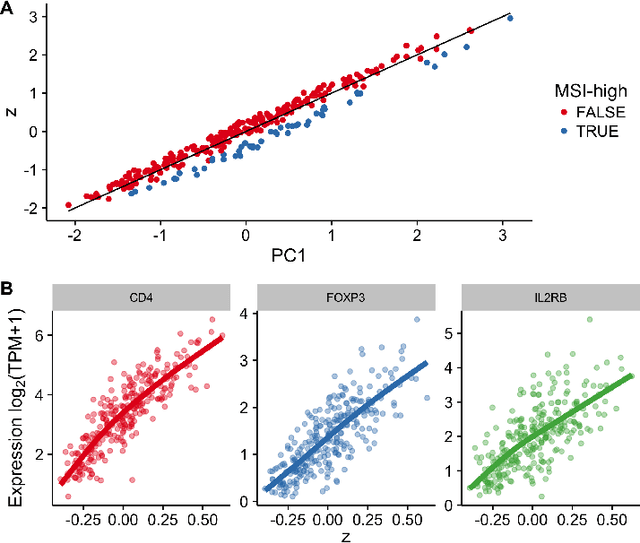
Standard models assign disease progression to discrete categories or stages based on well-characterized clinical markers. However, such a system is potentially at odds with our understanding of the underlying biology, which in highly complex systems may support a (near-)continuous evolution of disease from inception to terminal state. To learn such a continuous disease score one could infer a latent variable from dynamic "omics" data such as RNA-seq that correlates with an outcome of interest such as survival time. However, such analyses may be confounded by additional data such as clinical covariates measured in electronic health records (EHRs). As a solution to this we introduce covariate latent variable models, a novel type of latent variable model that learns a low-dimensional data representation in the presence of two (asymmetric) views of the same data source. We apply our model to TCGA colorectal cancer RNA-seq data and demonstrate how incorporating microsatellite-instability (MSI) status as an external covariate allows us to identify genes that stratify patients on an immune-response trajectory. Finally, we propose an extension termed Covariate Gaussian Process Latent Variable Models for learning nonparametric, nonlinear representations. An R package implementing variational inference for covariate latent variable models is available at http://github.com/kieranrcampbell/clvm.