Continual learning via probabilistic exchangeable sequence modelling

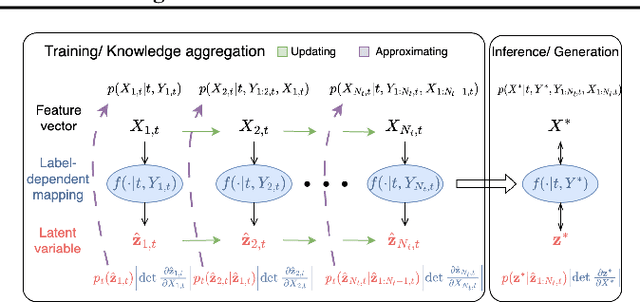
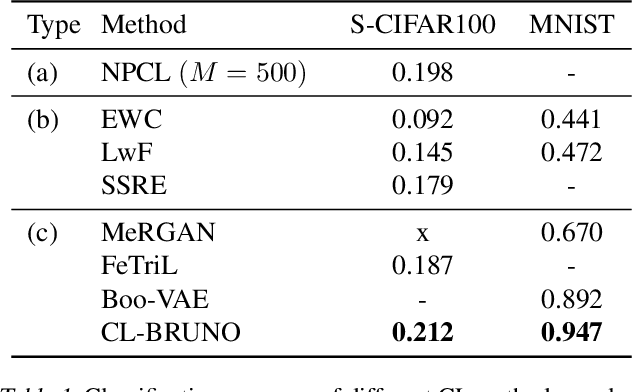
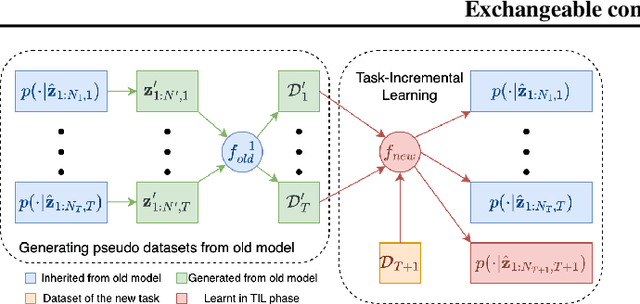
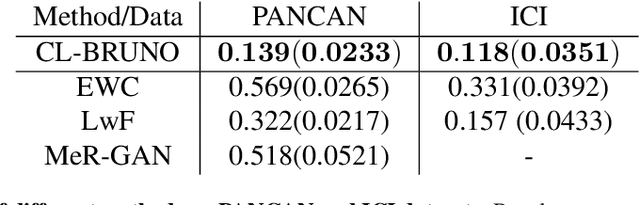
Continual learning (CL) refers to the ability to continuously learn and accumulate new knowledge while retaining useful information from past experiences. Although numerous CL methods have been proposed in recent years, it is not straightforward to deploy them directly to real-world decision-making problems due to their computational cost and lack of uncertainty quantification. To address these issues, we propose CL-BRUNO, a probabilistic, Neural Process-based CL model that performs scalable and tractable Bayesian update and prediction. Our proposed approach uses deep-generative models to create a unified probabilistic framework capable of handling different types of CL problems such as task- and class-incremental learning, allowing users to integrate information across different CL scenarios using a single model. Our approach is able to prevent catastrophic forgetting through distributional and functional regularisation without the need of retaining any previously seen samples, making it appealing to applications where data privacy or storage capacity is of concern. Experiments show that CL-BRUNO outperforms existing methods on both natural image and biomedical data sets, confirming its effectiveness in real-world applications.

A Transformer-based survival model for prediction of all-cause mortality in heart failure patients: a multi-cohort study

We developed and validated TRisk, a Transformer-based AI model predicting 36-month mortality in heart failure patients by analysing temporal patient journeys from UK electronic health records (EHR). Our study included 403,534 heart failure patients (ages 40-90) from 1,418 English general practices, with 1,063 practices for model derivation and 355 for external validation. TRisk was compared against the MAGGIC-EHR model across various patient subgroups. With median follow-up of 9 months, TRisk achieved a concordance index of 0.845 (95% confidence interval: [0.841, 0.849]), significantly outperforming MAGGIC-EHR's 0.728 (0.723, 0.733) for predicting 36-month all-cause mortality. TRisk showed more consistent performance across sex, age, and baseline characteristics, suggesting less bias. We successfully adapted TRisk to US hospital data through transfer learning, achieving a C-index of 0.802 (0.789, 0.816) with 21,767 patients. Explainability analyses revealed TRisk captured established risk factors while identifying underappreciated predictors like cancers and hepatic failure that were important across both cohorts. Notably, cancers maintained strong prognostic value even a decade after diagnosis. TRisk demonstrated well-calibrated mortality prediction across both healthcare systems. Our findings highlight the value of tracking longitudinal health profiles and revealed risk factors not included in previous expert-driven models.

Wave-LSTM: Multi-scale analysis of somatic whole genome copy number profiles

Changes in the number of copies of certain parts of the genome, known as copy number alterations (CNAs), due to somatic mutation processes are a hallmark of many cancers. This genomic complexity is known to be associated with poorer outcomes for patients but describing its contribution in detail has been difficult. Copy number alterations can affect large regions spanning whole chromosomes or the entire genome itself but can also be localised to only small segments of the genome and no methods exist that allow this multi-scale nature to be quantified. In this paper, we address this using Wave-LSTM, a signal decomposition approach designed to capture the multi-scale structure of complex whole genome copy number profiles. Using wavelet-based source separation in combination with deep learning-based attention mechanisms. We show that Wave-LSTM can be used to derive multi-scale representations from copy number profiles which can be used to decipher sub-clonal structures from single-cell copy number data and to improve survival prediction performance from patient tumour profiles.

Disentangling shared and private latent factors in multimodal Variational Autoencoders

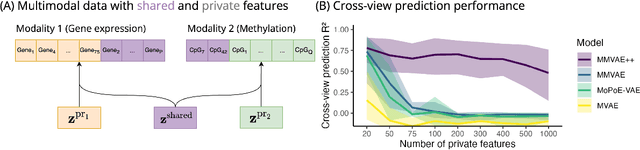
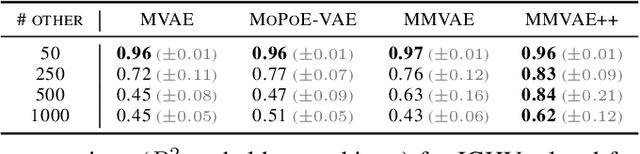
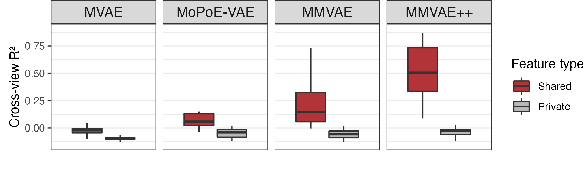
Generative models for multimodal data permit the identification of latent factors that may be associated with important determinants of observed data heterogeneity. Common or shared factors could be important for explaining variation across modalities whereas other factors may be private and important only for the explanation of a single modality. Multimodal Variational Autoencoders, such as MVAE and MMVAE, are a natural choice for inferring those underlying latent factors and separating shared variation from private. In this work, we investigate their capability to reliably perform this disentanglement. In particular, we highlight a challenging problem setting where modality-specific variation dominates the shared signal. Taking a cross-modal prediction perspective, we demonstrate limitations of existing models, and propose a modification how to make them more robust to modality-specific variation. Our findings are supported by experiments on synthetic as well as various real-world multi-omics data sets.

A Multi-Resolution Framework for U-Nets with Applications to Hierarchical VAEs

U-Net architectures are ubiquitous in state-of-the-art deep learning, however their regularisation properties and relationship to wavelets are understudied. In this paper, we formulate a multi-resolution framework which identifies U-Nets as finite-dimensional truncations of models on an infinite-dimensional function space. We provide theoretical results which prove that average pooling corresponds to projection within the space of square-integrable functions and show that U-Nets with average pooling implicitly learn a Haar wavelet basis representation of the data. We then leverage our framework to identify state-of-the-art hierarchical VAEs (HVAEs), which have a U-Net architecture, as a type of two-step forward Euler discretisation of multi-resolution diffusion processes which flow from a point mass, introducing sampling instabilities. We also demonstrate that HVAEs learn a representation of time which allows for improved parameter efficiency through weight-sharing. We use this observation to achieve state-of-the-art HVAE performance with half the number of parameters of existing models, exploiting the properties of our continuous-time formulation.

Multi-Facet Clustering Variational Autoencoders

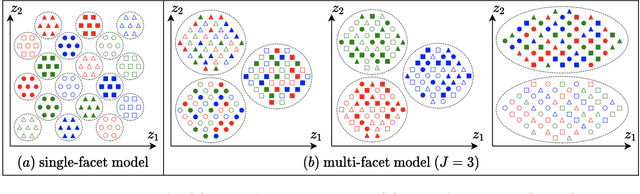
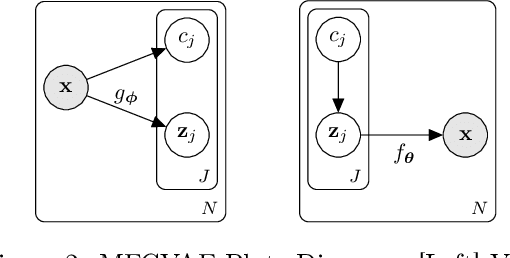
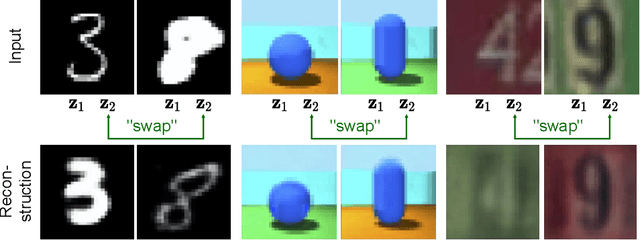
Work in deep clustering focuses on finding a single partition of data. However, high-dimensional data, such as images, typically feature multiple interesting characteristics one could cluster over. For example, images of objects against a background could be clustered over the shape of the object and separately by the colour of the background. In this paper, we introduce Multi-Facet Clustering Variational Autoencoders (MFCVAE), a novel class of variational autoencoders with a hierarchy of latent variables, each with a Mixture-of-Gaussians prior, that learns multiple clusterings simultaneously, and is trained fully unsupervised and end-to-end. MFCVAE uses a progressively-trained ladder architecture which leads to highly stable performance. We provide novel theoretical results for optimising the ELBO analytically with respect to the categorical variational posterior distribution, and corrects earlier influential theoretical work. On image benchmarks, we demonstrate that our approach separates out and clusters over different aspects of the data in a disentangled manner. We also show other advantages of our model: the compositionality of its latent space and that it provides controlled generation of samples.

Neural Decomposition: Functional ANOVA with Variational Autoencoders

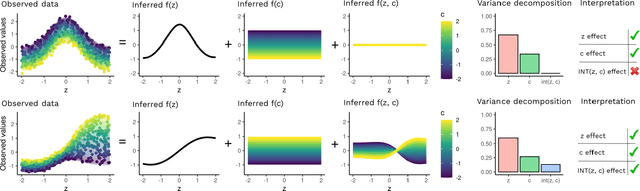
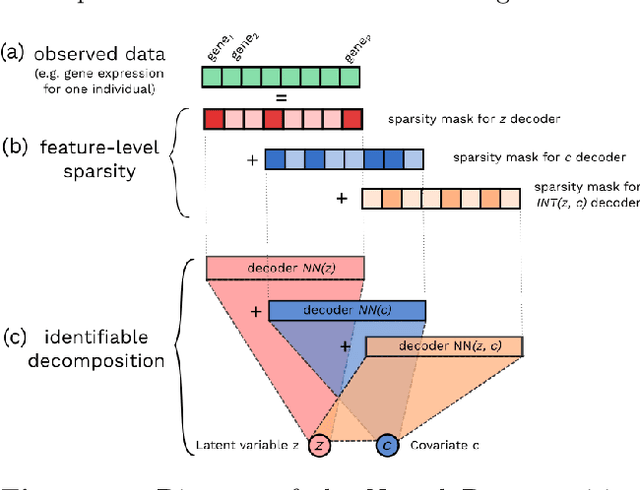
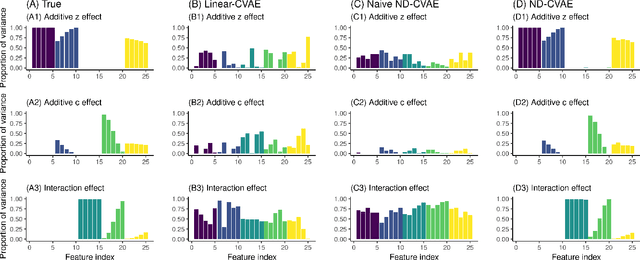
Variational Autoencoders (VAEs) have become a popular approach for dimensionality reduction. However, despite their ability to identify latent low-dimensional structures embedded within high-dimensional data, these latent representations are typically hard to interpret on their own. Due to the black-box nature of VAEs, their utility for healthcare and genomics applications has been limited. In this paper, we focus on characterising the sources of variation in Conditional VAEs. Our goal is to provide a feature-level variance decomposition, i.e. to decompose variation in the data by separating out the marginal additive effects of latent variables z and fixed inputs c from their non-linear interactions. We propose to achieve this through what we call Neural Decomposition - an adaptation of the well-known concept of functional ANOVA variance decomposition from classical statistics to deep learning models. We show how identifiability can be achieved by training models subject to constraints on the marginal properties of the decoder networks. We demonstrate the utility of our Neural Decomposition on a series of synthetic examples as well as high-dimensional genomics data.

BasisVAE: Translation-invariant feature-level clustering with Variational Autoencoders

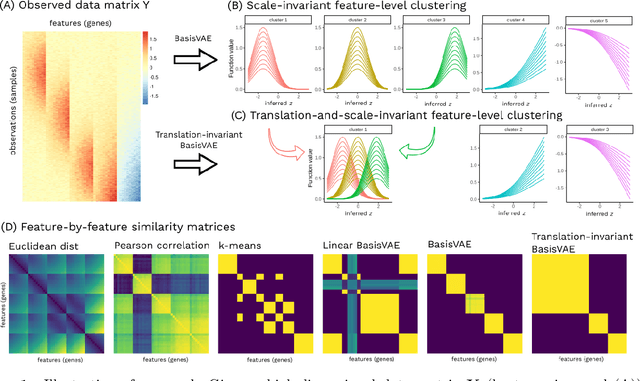
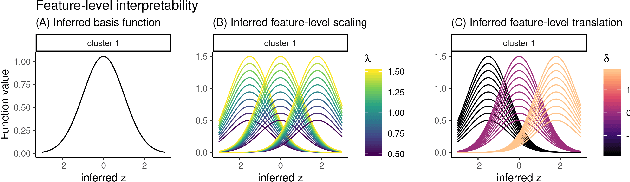
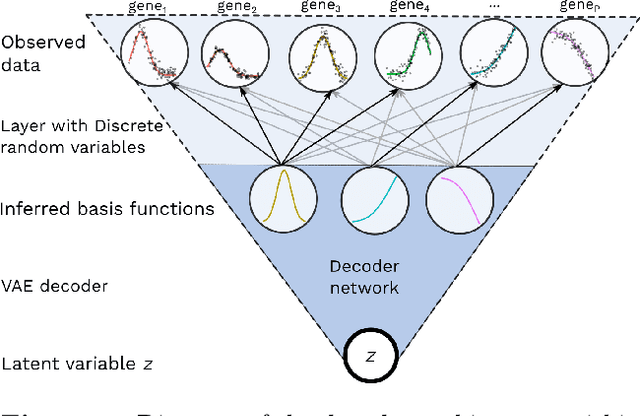
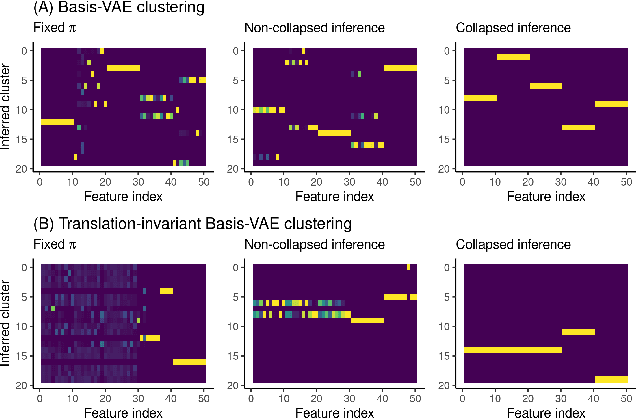
Variational Autoencoders (VAEs) provide a flexible and scalable framework for non-linear dimensionality reduction. However, in application domains such as genomics where data sets are typically tabular and high-dimensional, a black-box approach to dimensionality reduction does not provide sufficient insights. Common data analysis workflows additionally use clustering techniques to identify groups of similar features. This usually leads to a two-stage process, however, it would be desirable to construct a joint modelling framework for simultaneous dimensionality reduction and clustering of features. In this paper, we propose to achieve this through the BasisVAE: a combination of the VAE and a probabilistic clustering prior, which lets us learn a one-hot basis function representation as part of the decoder network. Furthermore, for scenarios where not all features are aligned, we develop an extension to handle translation-invariant basis functions. We show how a collapsed variational inference scheme leads to scalable and efficient inference for BasisVAE, demonstrated on various toy examples as well as on single-cell gene expression data.

Bayesian Nonparametric Boolean Factor Models

We build upon probabilistic models for Boolean Matrix and Boolean Tensor factorisation that have recently been shown to solve these problems with unprecedented accuracy and to enable posterior inference to scale to Billions of observation. Here, we lift the restriction of a pre-specified number of latent dimensions by introducing an Indian Buffet Process prior over factor matrices. Not only does the full factor-conditional take a computationally convenient form due to the logical dependencies in the model, but also the posterior over the number of non-zero latent dimensions is remarkably simple. It amounts to counting the number false and true negative predictions, whereas positive predictions can be ignored. This constitutes a very transparent example of sampling-based posterior inference with an IBP prior and, importantly, lets us maintain extremely efficient inference. We discuss applications to simulated data, as well as to a real world data matrix with 6 Million entries.

Covariate Gaussian Process Latent Variable Models

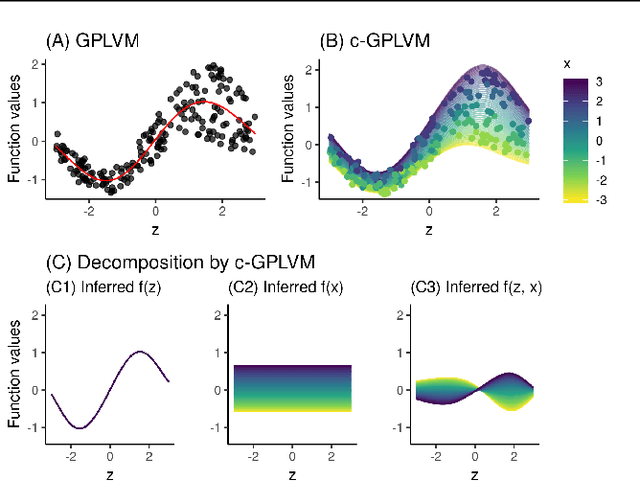
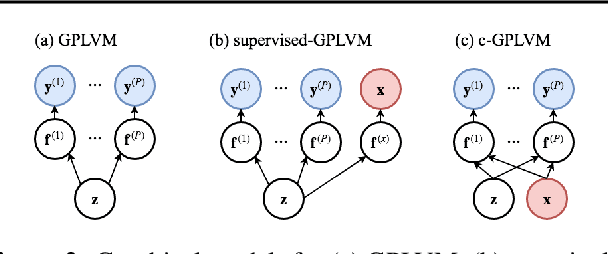
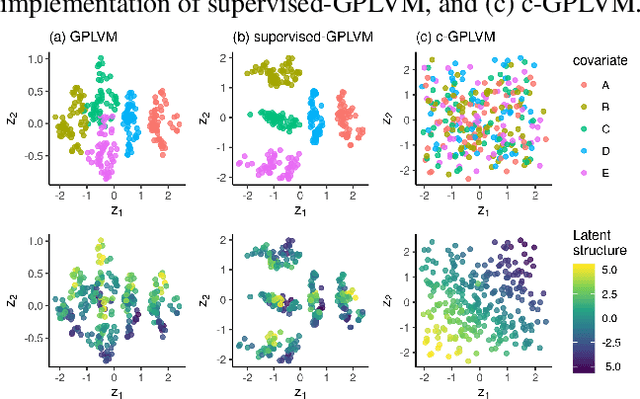
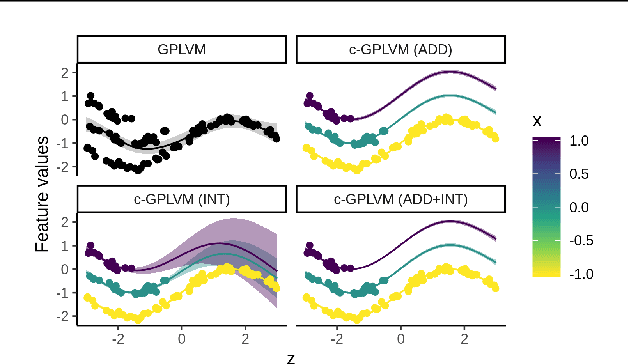
Gaussian Process Regression (GPR) and Gaussian Process Latent Variable Models (GPLVM) offer a principled way of performing probabilistic non-linear regression and dimensionality reduction. In this paper we propose a hybrid between the two, the covariate-GPLVM (c-GPLVM), to perform dimensionality reduction in the presence of covariate information (e.g. continuous covariates, class labels, or censored survival times). This construction lets us adjust for covariate effects and reveals meaningful latent structure which is not revealed when using GPLVM. Furthermore, we introduce structured decomposable kernels which will let us interpret how the fixed and latent inputs contribute to feature-level variation, e.g. identify the presence of a non-linear interaction. We demonstrate the utility of this model on applications in disease progression modelling from high-dimensional gene expression data in the presence of additional phenotypes.