Wave-LSTM: Multi-scale analysis of somatic whole genome copy number profiles

Changes in the number of copies of certain parts of the genome, known as copy number alterations (CNAs), due to somatic mutation processes are a hallmark of many cancers. This genomic complexity is known to be associated with poorer outcomes for patients but describing its contribution in detail has been difficult. Copy number alterations can affect large regions spanning whole chromosomes or the entire genome itself but can also be localised to only small segments of the genome and no methods exist that allow this multi-scale nature to be quantified. In this paper, we address this using Wave-LSTM, a signal decomposition approach designed to capture the multi-scale structure of complex whole genome copy number profiles. Using wavelet-based source separation in combination with deep learning-based attention mechanisms. We show that Wave-LSTM can be used to derive multi-scale representations from copy number profiles which can be used to decipher sub-clonal structures from single-cell copy number data and to improve survival prediction performance from patient tumour profiles.

Sample-efficient reinforcement learning using deep Gaussian processes

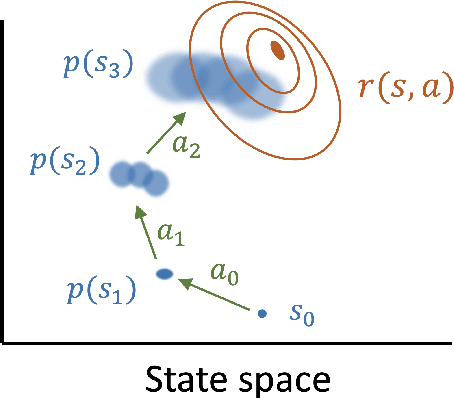
Reinforcement learning provides a framework for learning to control which actions to take towards completing a task through trial-and-error. In many applications observing interactions is costly, necessitating sample-efficient learning. In model-based reinforcement learning efficiency is improved by learning to simulate the world dynamics. The challenge is that model inaccuracies rapidly accumulate over planned trajectories. We introduce deep Gaussian processes where the depth of the compositions introduces model complexity while incorporating prior knowledge on the dynamics brings smoothness and structure. Our approach is able to sample a Bayesian posterior over trajectories. We demonstrate highly improved early sample-efficiency over competing methods. This is shown across a number of continuous control tasks, including the half-cheetah whose contact dynamics have previously posed an insurmountable problem for earlier sample-efficient Gaussian process based models.

Pseudo-marginal Bayesian inference for supervised Gaussian process latent variable models

We introduce a Bayesian framework for inference with a supervised version of the Gaussian process latent variable model. The framework overcomes the high correlations between latent variables and hyperparameters by using an unbiased pseudo estimate for the marginal likelihood that approximately integrates over the latent variables. This is used to construct a Markov Chain to explore the posterior of the hyperparameters. We demonstrate the procedure on simulated and real examples, showing its ability to capture uncertainty and multimodality of the hyperparameters and improved uncertainty quantification in predictions when compared with variational inference.