Latent mixed-effect models for high-dimensional longitudinal data

Modelling longitudinal data is an important yet challenging task. These datasets can be high-dimensional, contain non-linear effects and time-varying covariates. Gaussian process (GP) prior-based variational autoencoders (VAEs) have emerged as a promising approach due to their ability to model time-series data. However, they are costly to train and struggle to fully exploit the rich covariates characteristic of longitudinal data, making them difficult for practitioners to use effectively. In this work, we leverage linear mixed models (LMMs) and amortized variational inference to provide conditional priors for VAEs, and propose LMM-VAE, a scalable, interpretable and identifiable model. We highlight theoretical connections between it and GP-based techniques, providing a unified framework for this class of methods. Our proposal performs competitively compared to existing approaches across simulated and real-world datasets.

Modeling Randomly Observed Spatiotemporal Dynamical Systems

Spatiotemporal processes are a fundamental tool for modeling dynamics across various domains, from heat propagation in materials to oceanic and atmospheric flows. However, currently available neural network-based modeling approaches fall short when faced with data collected randomly over time and space, as is often the case with sensor networks in real-world applications like crowdsourced earthquake detection or pollution monitoring. In response, we developed a new spatiotemporal method that effectively handles such randomly sampled data. Our model integrates techniques from amortized variational inference, neural differential equations, neural point processes, and implicit neural representations to predict both the dynamics of the system and the probabilistic locations and timings of future observations. It outperforms existing methods on challenging spatiotemporal datasets by offering substantial improvements in predictive accuracy and computational efficiency, making it a useful tool for modeling and understanding complex dynamical systems observed under realistic, unconstrained conditions.

Field-based Molecule Generation

This work introduces FMG, a field-based model for drug-like molecule generation. We show how the flexibility of this method provides crucial advantages over the prevalent, point-cloud based methods, and achieves competitive molecular stability generation. We tackle optical isomerism (enantiomers), a previously omitted molecular property that is crucial for drug safety and effectiveness, and thus account for all molecular geometry aspects. We demonstrate how previous methods are invariant to a group of transformations that includes enantiomer pairs, leading them invariant to the molecular R and S configurations, while our field-based generative model captures this property.

Latent variable model for high-dimensional point process with structured missingness

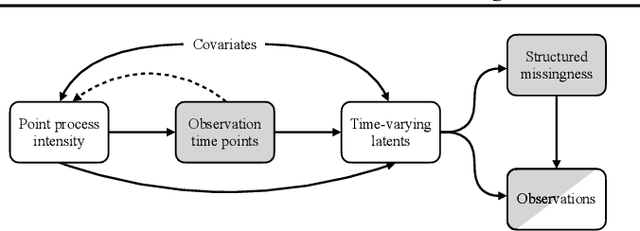
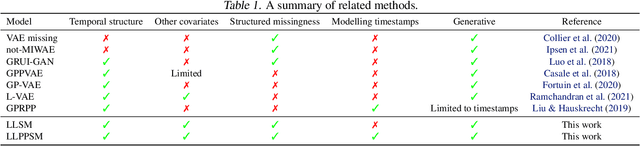
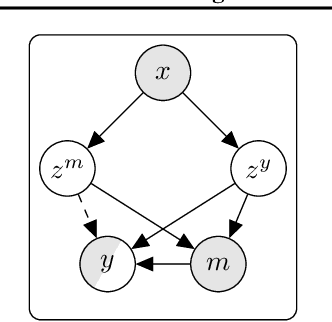
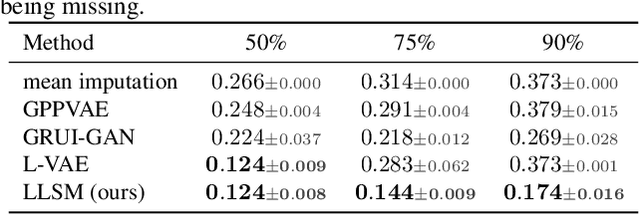
Longitudinal data are important in numerous fields, such as healthcare, sociology and seismology, but real-world datasets present notable challenges for practitioners because they can be high-dimensional, contain structured missingness patterns, and measurement time points can be governed by an unknown stochastic process. While various solutions have been suggested, the majority of them have been designed to account for only one of these challenges. In this work, we propose a flexible and efficient latent-variable model that is capable of addressing all these limitations. Our approach utilizes Gaussian processes to capture temporal correlations between samples and their associated missingness masks as well as to model the underlying point process. We construct our model as a variational autoencoder together with deep neural network parameterised encoder and decoder models, and develop a scalable amortised variational inference approach for efficient model training. We demonstrate competitive performance using both simulated and real datasets.

Estimating treatment effects from single-arm trials via latent-variable modeling

Randomized controlled trials (RCTs) are the accepted standard for treatment effect estimation but they can be infeasible due to ethical reasons and prohibitive costs. Single-arm trials, where all patients belong to the treatment group, can be a viable alternative but require access to an external control group. We propose an identifiable deep latent-variable model for this scenario that can also account for missing covariate observations by modeling their structured missingness patterns. Our method uses amortized variational inference to learn both group-specific and identifiable shared latent representations, which can subsequently be used for (i) patient matching if treatment outcomes are not available for the treatment group, or for (ii) direct treatment effect estimation assuming outcomes are available for both groups. We evaluate the model on a public benchmark as well as on a data set consisting of a published RCT study and real-world electronic health records. Compared to previous methods, our results show improved performance both for direct treatment effect estimation as well as for effect estimation via patient matching.

Learning Space-Time Continuous Neural PDEs from Partially Observed States

We introduce a novel grid-independent model for learning partial differential equations (PDEs) from noisy and partial observations on irregular spatiotemporal grids. We propose a space-time continuous latent neural PDE model with an efficient probabilistic framework and a novel encoder design for improved data efficiency and grid independence. The latent state dynamics are governed by a PDE model that combines the collocation method and the method of lines. We employ amortized variational inference for approximate posterior estimation and utilize a multiple shooting technique for enhanced training speed and stability. Our model demonstrates state-of-the-art performance on complex synthetic and real-world datasets, overcoming limitations of previous approaches and effectively handling partially-observed data. The proposed model outperforms recent methods, showing its potential to advance data-driven PDE modeling and enabling robust, grid-independent modeling of complex partially-observed dynamic processes.

Latent Neural ODEs with Sparse Bayesian Multiple Shooting

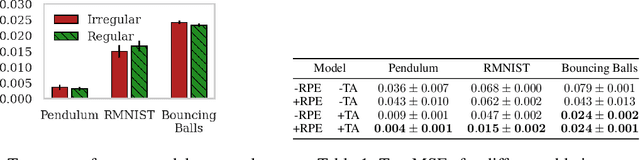
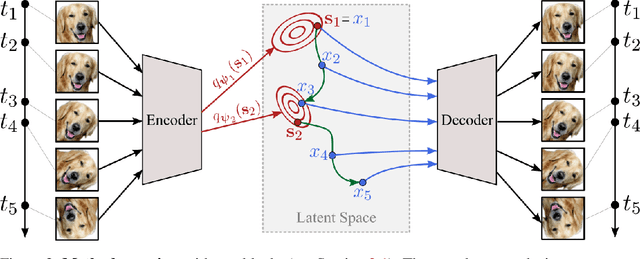
Training dynamic models, such as neural ODEs, on long trajectories is a hard problem that requires using various tricks, such as trajectory splitting, to make model training work in practice. These methods are often heuristics with poor theoretical justifications, and require iterative manual tuning. We propose a principled multiple shooting technique for neural ODEs that splits the trajectories into manageable short segments, which are optimised in parallel, while ensuring probabilistic control on continuity over consecutive segments. We derive variational inference for our shooting-based latent neural ODE models and propose amortized encodings of irregularly sampled trajectories with a transformer-based recognition network with temporal attention and relative positional encoding. We demonstrate efficient and stable training, and state-of-the-art performance on multiple large-scale benchmark datasets.

A Variational Autoencoder for Heterogeneous Temporal and Longitudinal Data

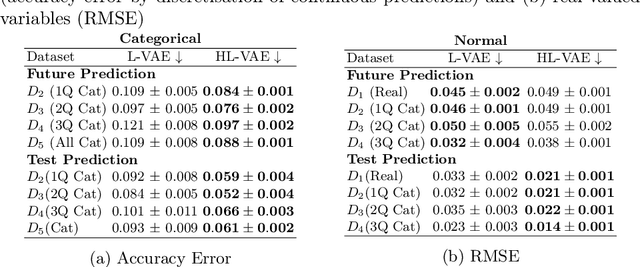
The variational autoencoder (VAE) is a popular deep latent variable model used to analyse high-dimensional datasets by learning a low-dimensional latent representation of the data. It simultaneously learns a generative model and an inference network to perform approximate posterior inference. Recently proposed extensions to VAEs that can handle temporal and longitudinal data have applications in healthcare, behavioural modelling, and predictive maintenance. However, these extensions do not account for heterogeneous data (i.e., data comprising of continuous and discrete attributes), which is common in many real-life applications. In this work, we propose the heterogeneous longitudinal VAE (HL-VAE) that extends the existing temporal and longitudinal VAEs to heterogeneous data. HL-VAE provides efficient inference for high-dimensional datasets and includes likelihood models for continuous, count, categorical, and ordinal data while accounting for missing observations. We demonstrate our model's efficacy through simulated as well as clinical datasets, and show that our proposed model achieves competitive performance in missing value imputation and predictive accuracy.

Learning Conditional Variational Autoencoders with Missing Covariates

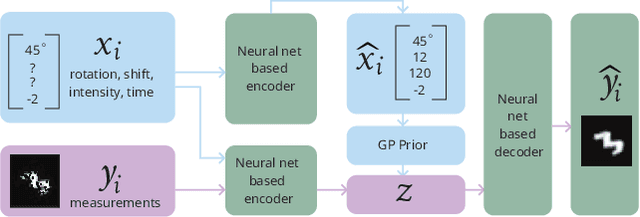
Conditional variational autoencoders (CVAEs) are versatile deep generative models that extend the standard VAE framework by conditioning the generative model with auxiliary covariates. The original CVAE model assumes that the data samples are independent, whereas more recent conditional VAE models, such as the Gaussian process (GP) prior VAEs, can account for complex correlation structures across all data samples. While several methods have been proposed to learn standard VAEs from partially observed datasets, these methods fall short for conditional VAEs. In this work, we propose a method to learn conditional VAEs from datasets in which auxiliary covariates can contain missing values as well. The proposed method augments the conditional VAEs with a prior distribution for the missing covariates and estimates their posterior using amortised variational inference. At training time, our method marginalises the uncertainty associated with the missing covariates while simultaneously maximising the evidence lower bound. We develop computationally efficient methods to learn CVAEs and GP prior VAEs that are compatible with mini-batching. Our experiments on simulated datasets as well as on a clinical trial study show that the proposed method outperforms previous methods in learning conditional VAEs from non-temporal, temporal, and longitudinal datasets.

Scalable mixed-domain Gaussian processes

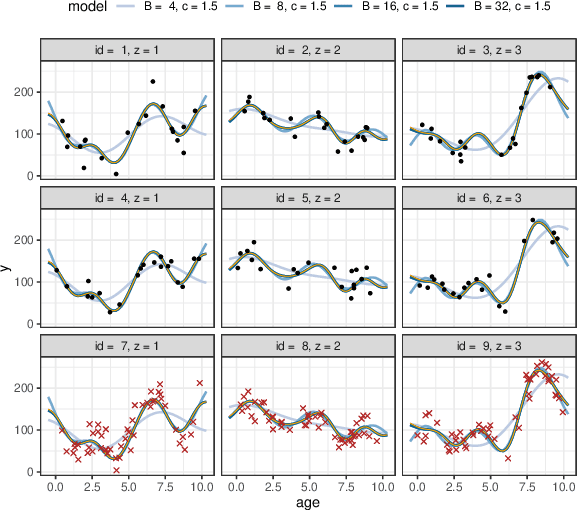
Gaussian process (GP) models that combine both categorical and continuous input variables have found use e.g. in longitudinal data analysis and computer experiments. However, standard inference for these models has the typical cubic scaling, and common scalable approximation schemes for GPs cannot be applied since the covariance function is non-continuous. In this work, we derive a basis function approximation scheme for mixed-domain covariance functions, which scales linearly with respect to the number of observations and total number of basis functions. The proposed approach is naturally applicable to Bayesian GP regression with arbitrary observation models. We demonstrate the approach in a longitudinal data modelling context and show that it approximates the exact GP model accurately, requiring only a fraction of the runtime compared to fitting the corresponding exact model.