Gleb Tikhonov
Learning Conditional Variational Autoencoders with Missing Covariates
Mar 02, 2022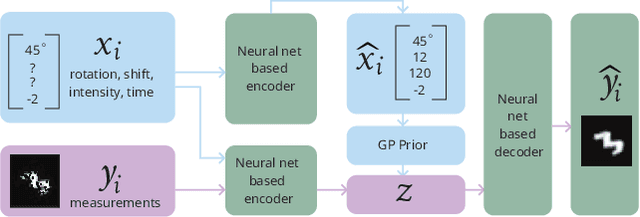



Abstract:Conditional variational autoencoders (CVAEs) are versatile deep generative models that extend the standard VAE framework by conditioning the generative model with auxiliary covariates. The original CVAE model assumes that the data samples are independent, whereas more recent conditional VAE models, such as the Gaussian process (GP) prior VAEs, can account for complex correlation structures across all data samples. While several methods have been proposed to learn standard VAEs from partially observed datasets, these methods fall short for conditional VAEs. In this work, we propose a method to learn conditional VAEs from datasets in which auxiliary covariates can contain missing values as well. The proposed method augments the conditional VAEs with a prior distribution for the missing covariates and estimates their posterior using amortised variational inference. At training time, our method marginalises the uncertainty associated with the missing covariates while simultaneously maximising the evidence lower bound. We develop computationally efficient methods to learn CVAEs and GP prior VAEs that are compatible with mini-batching. Our experiments on simulated datasets as well as on a clinical trial study show that the proposed method outperforms previous methods in learning conditional VAEs from non-temporal, temporal, and longitudinal datasets.
Longitudinal Variational Autoencoder
Jun 17, 2020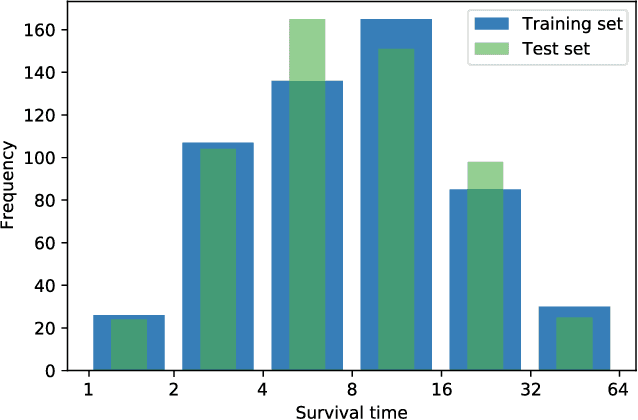

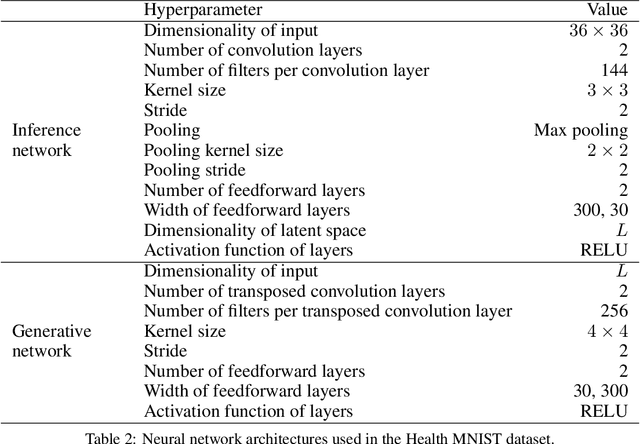
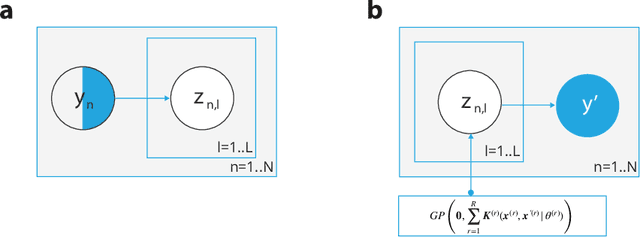
Abstract:Longitudinal datasets measured repeatedly over time from individual subjects, arise in many biomedical, psychological, social, and other studies. Such multivariate time-series are often high-dimensional and contain missing values. A common approach to analyse this kind of data is to learn a low-dimensional representation using variational autoencoders (VAEs). However, standard VAEs assume that the learned representations are i.i.d., and fail to capture the correlations between the data samples. We propose a novel deep generative model, Longitudinal VAE (L-VAE), that uses a multi-output additive Gaussian process (GP) prior to extend the VAE's capability to learn structured low-dimensional representations imposed by auxiliary covariate information, and also derive a new divergence upper bound for such GPs. Our approach can simultaneously accommodate both time-varying shared and random effects, produce structured low-dimensional representations, disentangle effects of individual covariates or their interactions, and achieve highly accurate predictive performance. We compare our model against previous methods on synthetic and clinical datasets, and demonstrate the state-of-the-art performance in data imputation, reconstruction, and long-term prediction tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge