Latent mixed-effect models for high-dimensional longitudinal data

Modelling longitudinal data is an important yet challenging task. These datasets can be high-dimensional, contain non-linear effects and time-varying covariates. Gaussian process (GP) prior-based variational autoencoders (VAEs) have emerged as a promising approach due to their ability to model time-series data. However, they are costly to train and struggle to fully exploit the rich covariates characteristic of longitudinal data, making them difficult for practitioners to use effectively. In this work, we leverage linear mixed models (LMMs) and amortized variational inference to provide conditional priors for VAEs, and propose LMM-VAE, a scalable, interpretable and identifiable model. We highlight theoretical connections between it and GP-based techniques, providing a unified framework for this class of methods. Our proposal performs competitively compared to existing approaches across simulated and real-world datasets.

Learning Conditional Variational Autoencoders with Missing Covariates

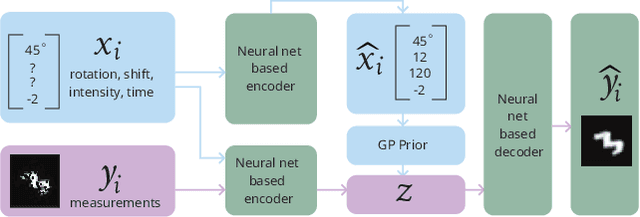
Conditional variational autoencoders (CVAEs) are versatile deep generative models that extend the standard VAE framework by conditioning the generative model with auxiliary covariates. The original CVAE model assumes that the data samples are independent, whereas more recent conditional VAE models, such as the Gaussian process (GP) prior VAEs, can account for complex correlation structures across all data samples. While several methods have been proposed to learn standard VAEs from partially observed datasets, these methods fall short for conditional VAEs. In this work, we propose a method to learn conditional VAEs from datasets in which auxiliary covariates can contain missing values as well. The proposed method augments the conditional VAEs with a prior distribution for the missing covariates and estimates their posterior using amortised variational inference. At training time, our method marginalises the uncertainty associated with the missing covariates while simultaneously maximising the evidence lower bound. We develop computationally efficient methods to learn CVAEs and GP prior VAEs that are compatible with mini-batching. Our experiments on simulated datasets as well as on a clinical trial study show that the proposed method outperforms previous methods in learning conditional VAEs from non-temporal, temporal, and longitudinal datasets.