Scalable mixed-domain Gaussian processes

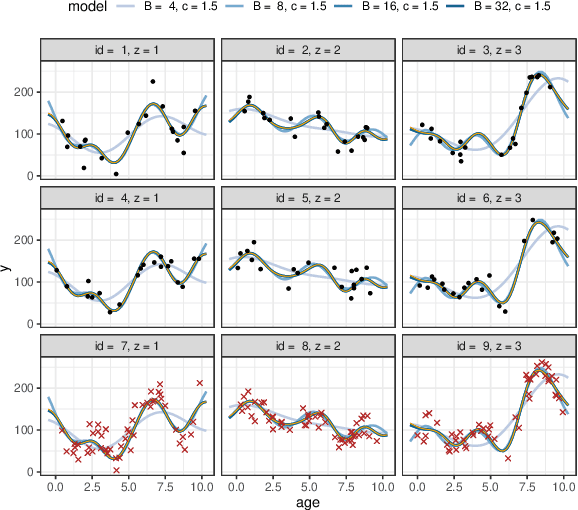
Gaussian process (GP) models that combine both categorical and continuous input variables have found use e.g. in longitudinal data analysis and computer experiments. However, standard inference for these models has the typical cubic scaling, and common scalable approximation schemes for GPs cannot be applied since the covariance function is non-continuous. In this work, we derive a basis function approximation scheme for mixed-domain covariance functions, which scales linearly with respect to the number of observations and total number of basis functions. The proposed approach is naturally applicable to Bayesian GP regression with arbitrary observation models. We demonstrate the approach in a longitudinal data modelling context and show that it approximates the exact GP model accurately, requiring only a fraction of the runtime compared to fitting the corresponding exact model.

An interpretable probabilistic machine learning method for heterogeneous longitudinal studies

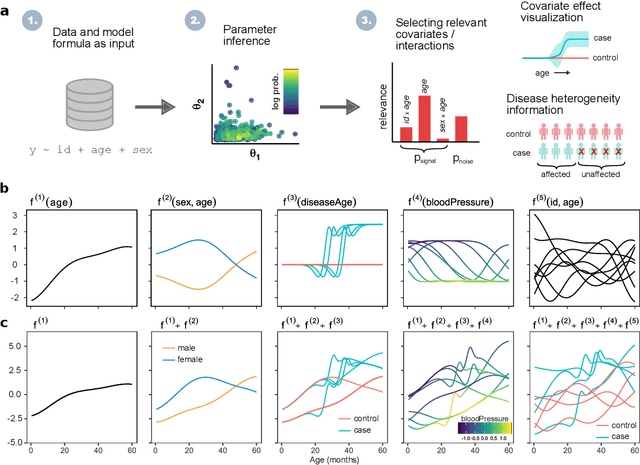
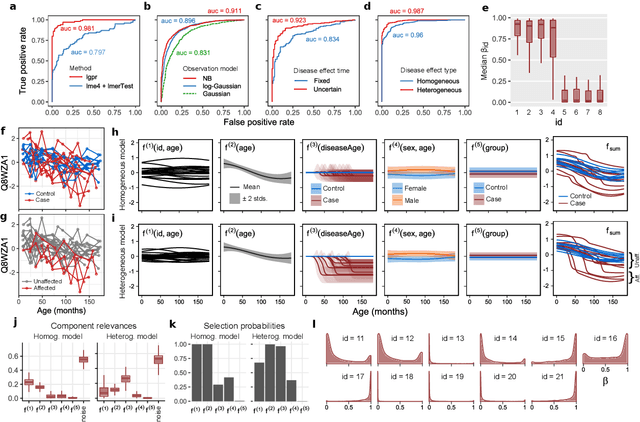
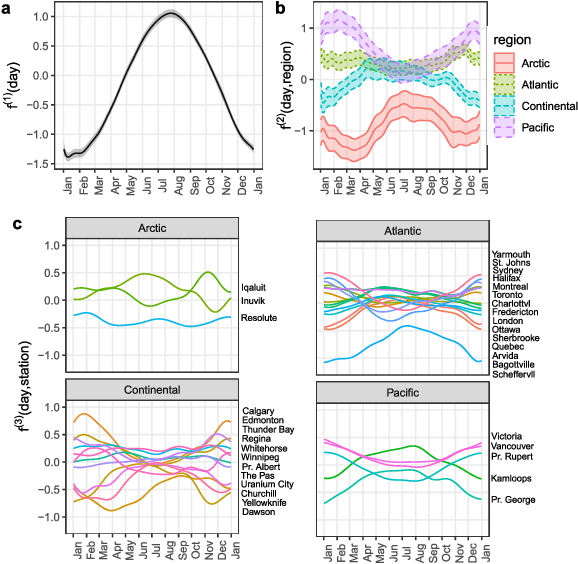
Identifying risk factors from longitudinal data requires statistical tools that are not restricted to linear models, yet provide interpretable associations between different types of covariates and a response variable. Here, we present a widely applicable and interpretable probabilistic machine learning method for nonparametric longitudinal data analysis using additive Gaussian process regression. We demonstrate that it outperforms previous longitudinal modeling approaches and provides useful novel features, including the ability to account for uncertainty in disease effect times as well as heterogeneity in their effects.