An interpretable probabilistic machine learning method for heterogeneous longitudinal studies

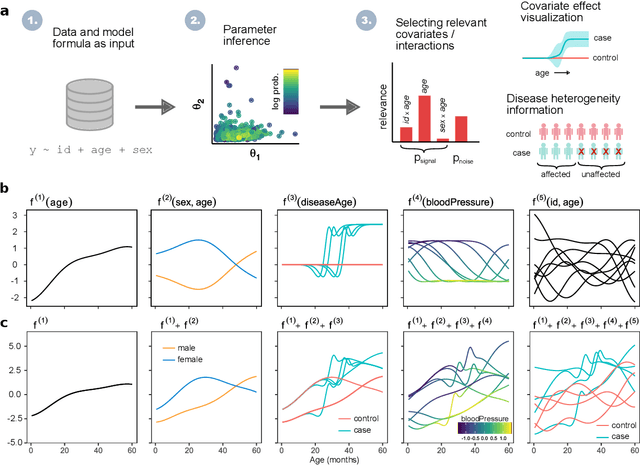
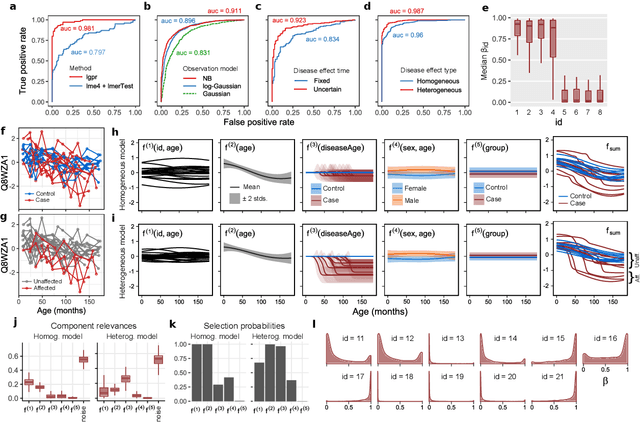
Identifying risk factors from longitudinal data requires statistical tools that are not restricted to linear models, yet provide interpretable associations between different types of covariates and a response variable. Here, we present a widely applicable and interpretable probabilistic machine learning method for nonparametric longitudinal data analysis using additive Gaussian process regression. We demonstrate that it outperforms previous longitudinal modeling approaches and provides useful novel features, including the ability to account for uncertainty in disease effect times as well as heterogeneity in their effects.

Learning Stochastic Differential Equations With Gaussian Processes Without Gradient Matching

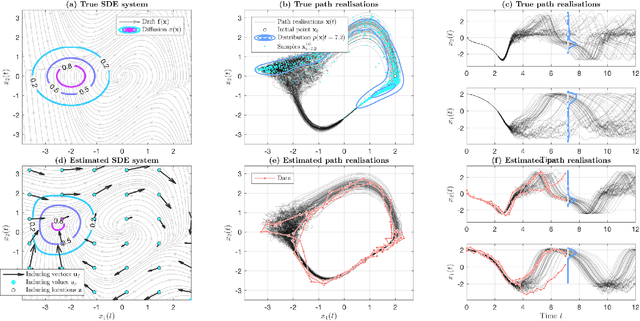
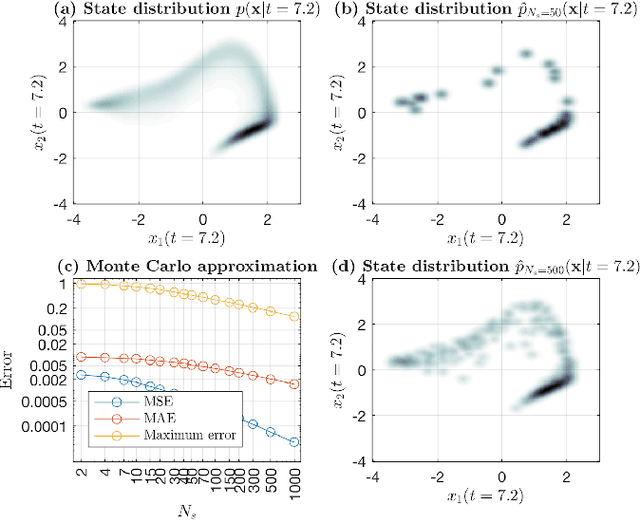
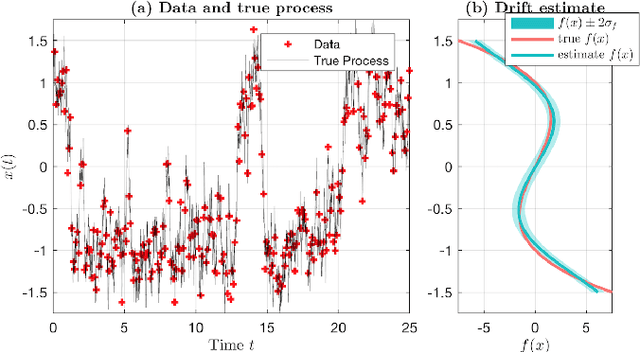
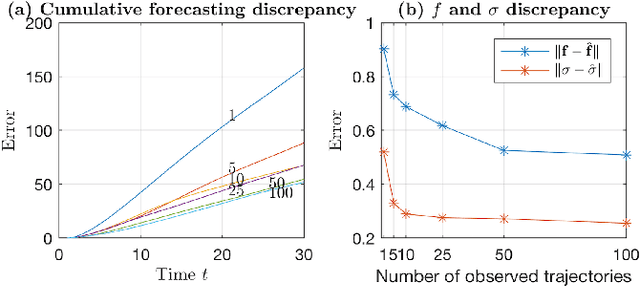
We introduce a novel paradigm for learning non-parametric drift and diffusion functions for stochastic differential equation (SDE). The proposed model learns to simulate path distributions that match observations with non-uniform time increments and arbitrary sparseness, which is in contrast with gradient matching that does not optimize simulated responses. We formulate sensitivity equations for learning and demonstrate that our general stochastic distribution optimisation leads to robust and efficient learning of SDE systems.

Bayesian Metabolic Flux Analysis reveals intracellular flux couplings

Metabolic flux balance analyses are a standard tool in analysing metabolic reaction rates compatible with measurements, steady-state and the metabolic reaction network stoichiometry. Flux analysis methods commonly place unrealistic assumptions on fluxes due to the convenience of formulating the problem as a linear programming model, and most methods ignore the notable uncertainty in flux estimates. We introduce a novel paradigm of Bayesian metabolic flux analysis that models the reactions of the whole genome-scale cellular system in probabilistic terms, and can infer the full flux vector distribution of genome-scale metabolic systems based on exchange and intracellular (e.g. 13C) flux measurements, steady-state assumptions, and target function assumptions. The Bayesian model couples all fluxes jointly together in a simple truncated multivariate posterior distribution, which reveals informative flux couplings. Our model is a plug-in replacement to conventional metabolic balance methods, such as flux balance analysis (FBA). Our experiments indicate that we can characterise the genome-scale flux covariances, reveal flux couplings, and determine more intracellular unobserved fluxes in C. acetobutylicum from 13C data than flux variability analysis. The COBRA compatible software is available at github.com/markusheinonen/bamfa

Learning unknown ODE models with Gaussian processes

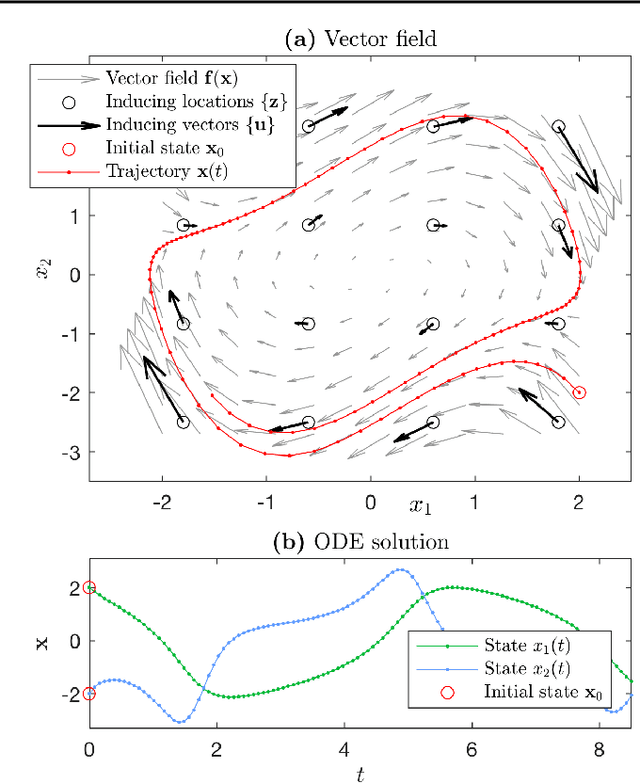
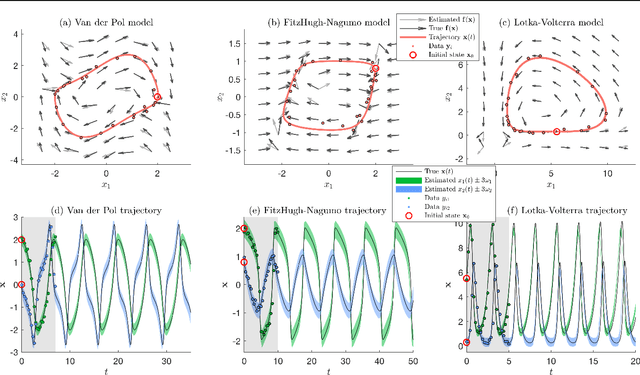
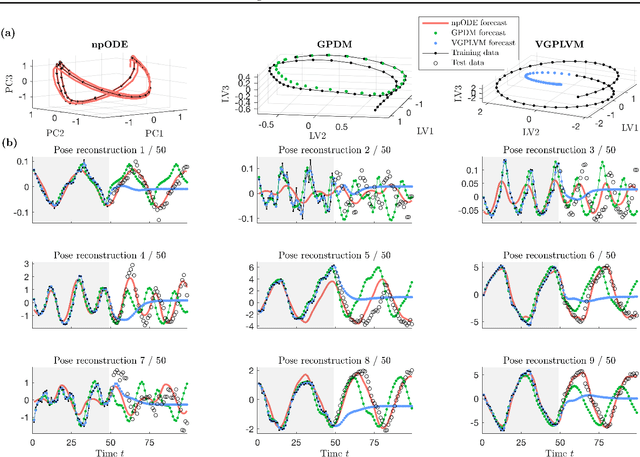
In conventional ODE modelling coefficients of an equation driving the system state forward in time are estimated. However, for many complex systems it is practically impossible to determine the equations or interactions governing the underlying dynamics. In these settings, parametric ODE model cannot be formulated. Here, we overcome this issue by introducing a novel paradigm of nonparametric ODE modelling that can learn the underlying dynamics of arbitrary continuous-time systems without prior knowledge. We propose to learn non-linear, unknown differential functions from state observations using Gaussian process vector fields within the exact ODE formalism. We demonstrate the model's capabilities to infer dynamics from sparse data and to simulate the system forward into future.

Non-Stationary Gaussian Process Regression with Hamiltonian Monte Carlo

We present a novel approach for fully non-stationary Gaussian process regression (GPR), where all three key parameters -- noise variance, signal variance and lengthscale -- can be simultaneously input-dependent. We develop gradient-based inference methods to learn the unknown function and the non-stationary model parameters, without requiring any model approximations. We propose to infer full parameter posterior with Hamiltonian Monte Carlo (HMC), which conveniently extends the analytical gradient-based GPR learning by guiding the sampling with model gradients. We also learn the MAP solution from the posterior by gradient ascent. In experiments on several synthetic datasets and in modelling of temporal gene expression, the nonstationary GPR is shown to be necessary for modeling realistic input-dependent dynamics, while it performs comparably to conventional stationary or previous non-stationary GPR models otherwise.