Latent Neural ODEs with Sparse Bayesian Multiple Shooting

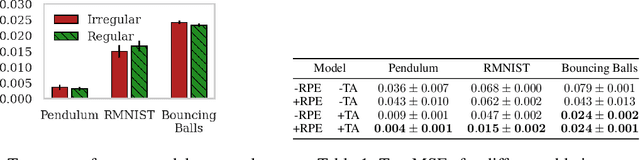
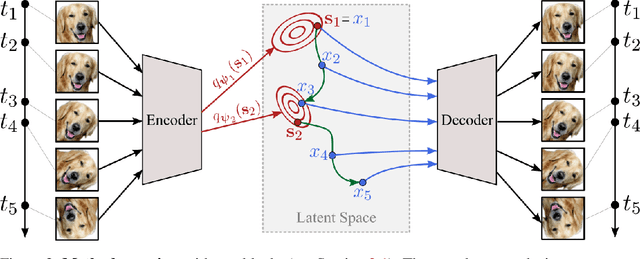
Training dynamic models, such as neural ODEs, on long trajectories is a hard problem that requires using various tricks, such as trajectory splitting, to make model training work in practice. These methods are often heuristics with poor theoretical justifications, and require iterative manual tuning. We propose a principled multiple shooting technique for neural ODEs that splits the trajectories into manageable short segments, which are optimised in parallel, while ensuring probabilistic control on continuity over consecutive segments. We derive variational inference for our shooting-based latent neural ODE models and propose amortized encodings of irregularly sampled trajectories with a transformer-based recognition network with temporal attention and relative positional encoding. We demonstrate efficient and stable training, and state-of-the-art performance on multiple large-scale benchmark datasets.

Learning Stochastic Differential Equations With Gaussian Processes Without Gradient Matching

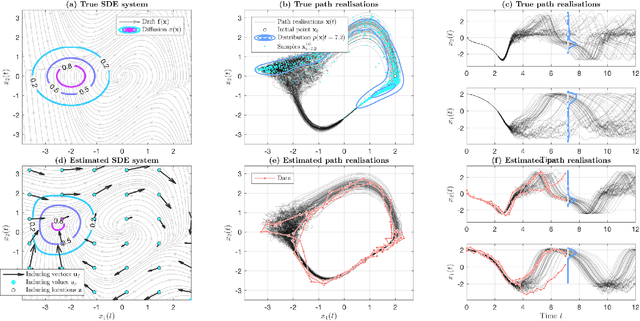
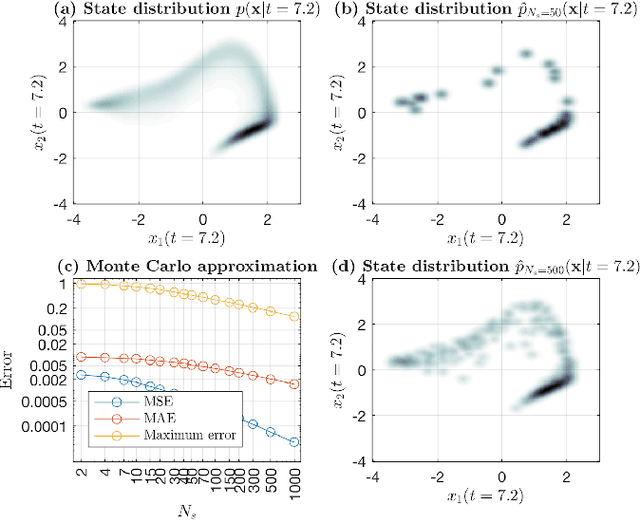
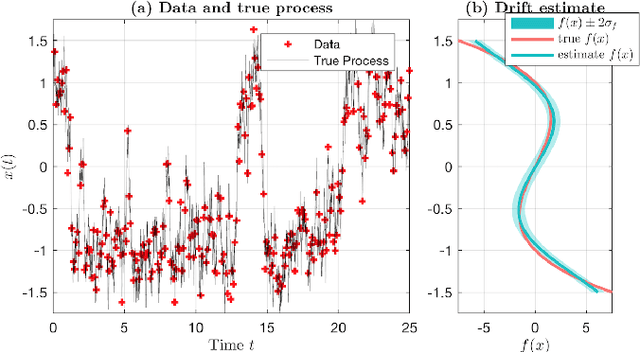
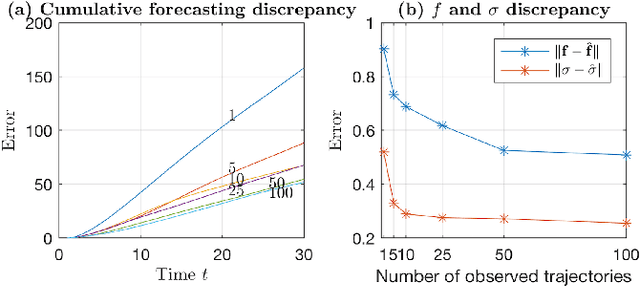
We introduce a novel paradigm for learning non-parametric drift and diffusion functions for stochastic differential equation (SDE). The proposed model learns to simulate path distributions that match observations with non-uniform time increments and arbitrary sparseness, which is in contrast with gradient matching that does not optimize simulated responses. We formulate sensitivity equations for learning and demonstrate that our general stochastic distribution optimisation leads to robust and efficient learning of SDE systems.

Learning unknown ODE models with Gaussian processes

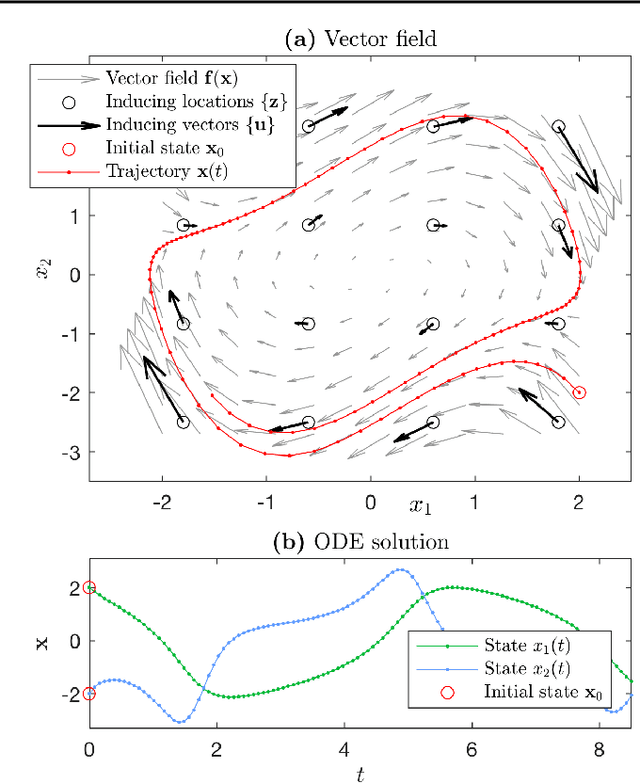
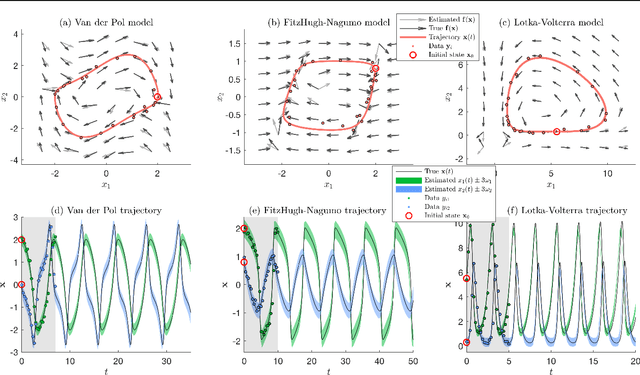
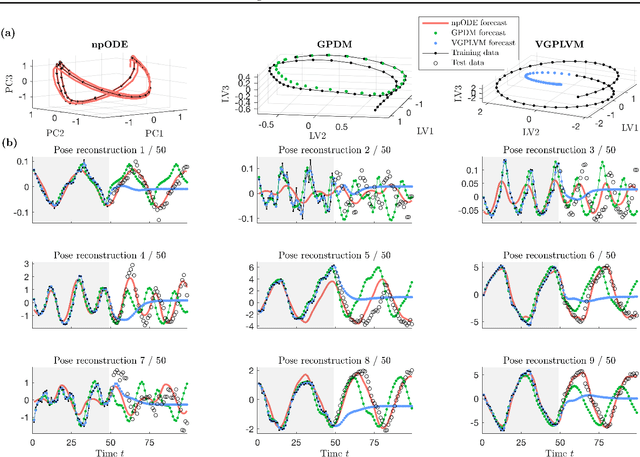
In conventional ODE modelling coefficients of an equation driving the system state forward in time are estimated. However, for many complex systems it is practically impossible to determine the equations or interactions governing the underlying dynamics. In these settings, parametric ODE model cannot be formulated. Here, we overcome this issue by introducing a novel paradigm of nonparametric ODE modelling that can learn the underlying dynamics of arbitrary continuous-time systems without prior knowledge. We propose to learn non-linear, unknown differential functions from state observations using Gaussian process vector fields within the exact ODE formalism. We demonstrate the model's capabilities to infer dynamics from sparse data and to simulate the system forward into future.