Learning Stochastic Differential Equations With Gaussian Processes Without Gradient Matching
Paper and Code
Jul 31, 2018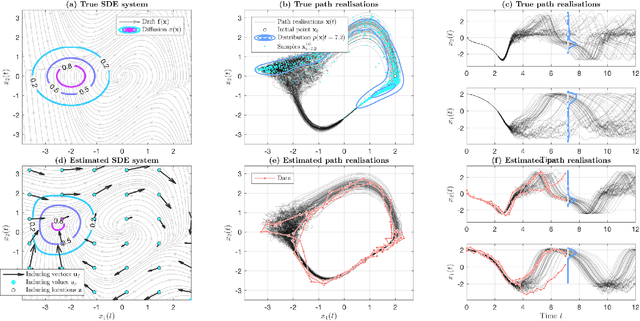
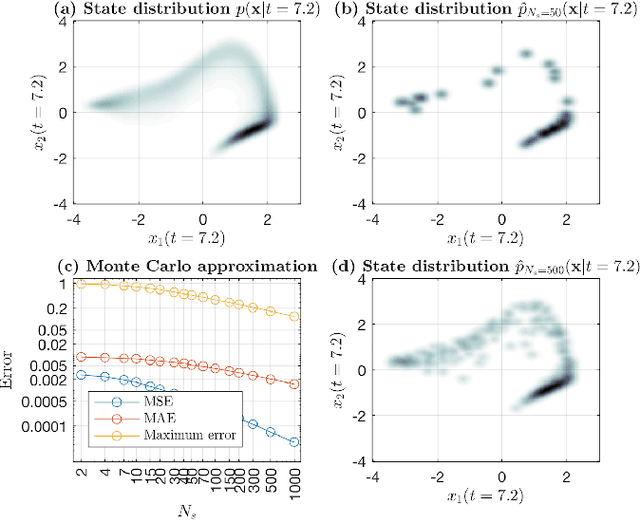
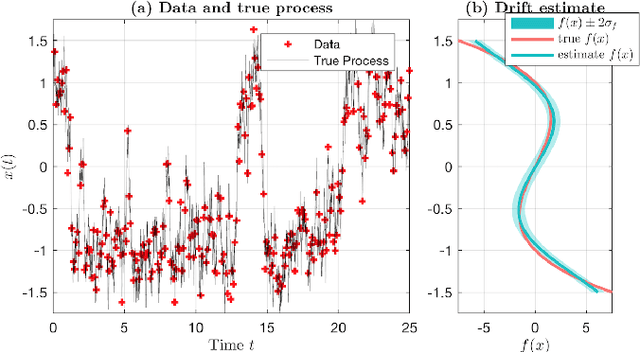
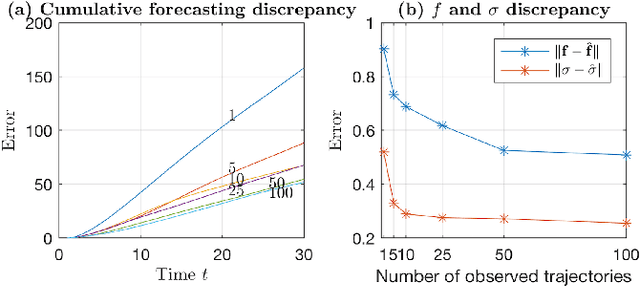
We introduce a novel paradigm for learning non-parametric drift and diffusion functions for stochastic differential equation (SDE). The proposed model learns to simulate path distributions that match observations with non-uniform time increments and arbitrary sparseness, which is in contrast with gradient matching that does not optimize simulated responses. We formulate sensitivity equations for learning and demonstrate that our general stochastic distribution optimisation leads to robust and efficient learning of SDE systems.
* The accepted version of the paper to be presented in 2018 IEEE
International Workshop on Machine Learning for Signal Processing
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge