Modeling Randomly Observed Spatiotemporal Dynamical Systems

Spatiotemporal processes are a fundamental tool for modeling dynamics across various domains, from heat propagation in materials to oceanic and atmospheric flows. However, currently available neural network-based modeling approaches fall short when faced with data collected randomly over time and space, as is often the case with sensor networks in real-world applications like crowdsourced earthquake detection or pollution monitoring. In response, we developed a new spatiotemporal method that effectively handles such randomly sampled data. Our model integrates techniques from amortized variational inference, neural differential equations, neural point processes, and implicit neural representations to predict both the dynamics of the system and the probabilistic locations and timings of future observations. It outperforms existing methods on challenging spatiotemporal datasets by offering substantial improvements in predictive accuracy and computational efficiency, making it a useful tool for modeling and understanding complex dynamical systems observed under realistic, unconstrained conditions.

Field-based Molecule Generation

This work introduces FMG, a field-based model for drug-like molecule generation. We show how the flexibility of this method provides crucial advantages over the prevalent, point-cloud based methods, and achieves competitive molecular stability generation. We tackle optical isomerism (enantiomers), a previously omitted molecular property that is crucial for drug safety and effectiveness, and thus account for all molecular geometry aspects. We demonstrate how previous methods are invariant to a group of transformations that includes enantiomer pairs, leading them invariant to the molecular R and S configurations, while our field-based generative model captures this property.

Learning Space-Time Continuous Neural PDEs from Partially Observed States

We introduce a novel grid-independent model for learning partial differential equations (PDEs) from noisy and partial observations on irregular spatiotemporal grids. We propose a space-time continuous latent neural PDE model with an efficient probabilistic framework and a novel encoder design for improved data efficiency and grid independence. The latent state dynamics are governed by a PDE model that combines the collocation method and the method of lines. We employ amortized variational inference for approximate posterior estimation and utilize a multiple shooting technique for enhanced training speed and stability. Our model demonstrates state-of-the-art performance on complex synthetic and real-world datasets, overcoming limitations of previous approaches and effectively handling partially-observed data. The proposed model outperforms recent methods, showing its potential to advance data-driven PDE modeling and enabling robust, grid-independent modeling of complex partially-observed dynamic processes.

Latent Neural ODEs with Sparse Bayesian Multiple Shooting

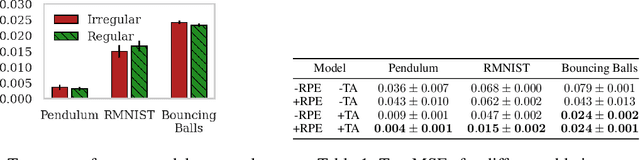
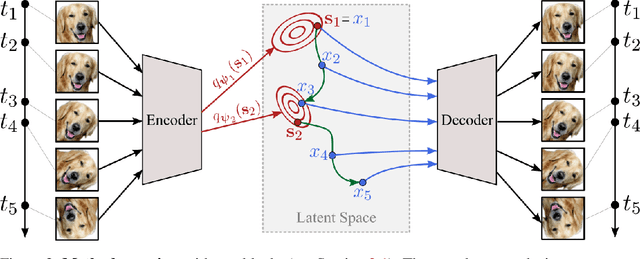
Training dynamic models, such as neural ODEs, on long trajectories is a hard problem that requires using various tricks, such as trajectory splitting, to make model training work in practice. These methods are often heuristics with poor theoretical justifications, and require iterative manual tuning. We propose a principled multiple shooting technique for neural ODEs that splits the trajectories into manageable short segments, which are optimised in parallel, while ensuring probabilistic control on continuity over consecutive segments. We derive variational inference for our shooting-based latent neural ODE models and propose amortized encodings of irregularly sampled trajectories with a transformer-based recognition network with temporal attention and relative positional encoding. We demonstrate efficient and stable training, and state-of-the-art performance on multiple large-scale benchmark datasets.

Learning continuous-time PDEs from sparse data with graph neural networks

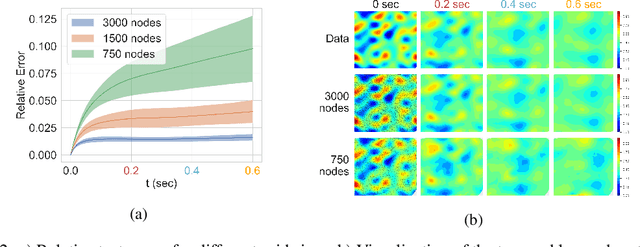
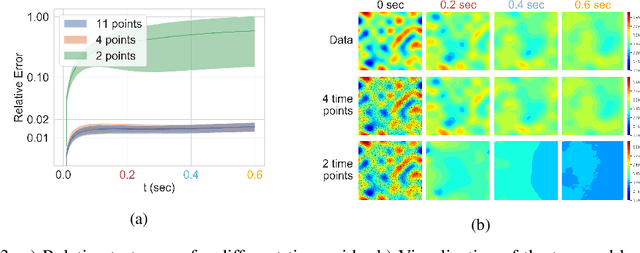
The behavior of many dynamical systems follow complex, yet still unknown partial differential equations (PDEs). While several machine learning methods have been proposed to learn PDEs directly from data, previous methods are limited to discrete-time approximations or make the limiting assumption of the observations arriving at regular grids. We propose a general continuous-time differential model for dynamical systems whose governing equations are parameterized by message passing graph neural networks. The model admits arbitrary space and time discretizations, which removes constraints on the locations of observation points and time intervals between the observations. The model is trained with continuous-time adjoint method enabling efficient neural PDE inference. We demonstrate the model's ability to work with unstructured grids, arbitrary time steps, and noisy observations. We compare our method with existing approaches on several well-known physical systems that involve first and higher-order PDEs with state-of-the-art predictive performance.