Learning continuous-time PDEs from sparse data with graph neural networks
Paper and Code
Jun 16, 2020

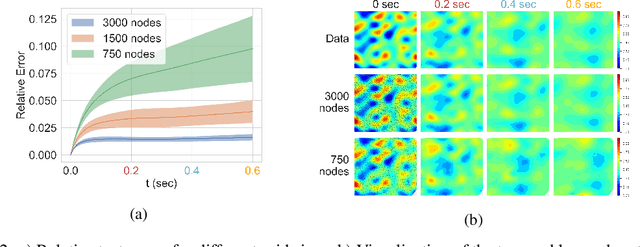
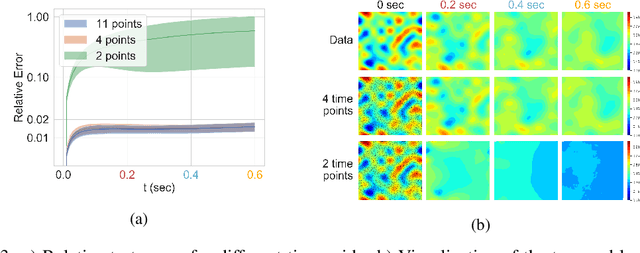
The behavior of many dynamical systems follow complex, yet still unknown partial differential equations (PDEs). While several machine learning methods have been proposed to learn PDEs directly from data, previous methods are limited to discrete-time approximations or make the limiting assumption of the observations arriving at regular grids. We propose a general continuous-time differential model for dynamical systems whose governing equations are parameterized by message passing graph neural networks. The model admits arbitrary space and time discretizations, which removes constraints on the locations of observation points and time intervals between the observations. The model is trained with continuous-time adjoint method enabling efficient neural PDE inference. We demonstrate the model's ability to work with unstructured grids, arbitrary time steps, and noisy observations. We compare our method with existing approaches on several well-known physical systems that involve first and higher-order PDEs with state-of-the-art predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge