MassSpecGym: A benchmark for the discovery and identification of molecules

The discovery and identification of molecules in biological and environmental samples is crucial for advancing biomedical and chemical sciences. Tandem mass spectrometry (MS/MS) is the leading technique for high-throughput elucidation of molecular structures. However, decoding a molecular structure from its mass spectrum is exceptionally challenging, even when performed by human experts. As a result, the vast majority of acquired MS/MS spectra remain uninterpreted, thereby limiting our understanding of the underlying (bio)chemical processes. Despite decades of progress in machine learning applications for predicting molecular structures from MS/MS spectra, the development of new methods is severely hindered by the lack of standard datasets and evaluation protocols. To address this problem, we propose MassSpecGym -- the first comprehensive benchmark for the discovery and identification of molecules from MS/MS data. Our benchmark comprises the largest publicly available collection of high-quality labeled MS/MS spectra and defines three MS/MS annotation challenges: \textit{de novo} molecular structure generation, molecule retrieval, and spectrum simulation. It includes new evaluation metrics and a generalization-demanding data split, therefore standardizing the MS/MS annotation tasks and rendering the problem accessible to the broad machine learning community. MassSpecGym is publicly available at \url{https://github.com/pluskal-lab/MassSpecGym}.

New methods for drug synergy prediction: a mini-review

In this mini-review, we explore the new prediction methods for drug combination synergy relying on high-throughput combinatorial screens. The fast progress of the field is witnessed in the more than thirty original machine learning methods published since 2021, a clear majority of them based on deep learning techniques. We aim to put these papers under a unifying lens by highlighting the core technologies, the data sources, the input data types and synergy scores used in the methods, as well as the prediction scenarios and evaluation protocols that the papers deal with. Our finding is that the best methods accurately solve the synergy prediction scenarios involving known drugs or cell lines while the scenarios involving new drugs or cell lines still fall short of an accurate prediction level.

Scalable variable selection for two-view learning tasks with projection operators

In this paper we propose a novel variable selection method for two-view settings, or for vector-valued supervised learning problems. Our framework is able to handle extremely large scale selection tasks, where number of data samples could be even millions. In a nutshell, our method performs variable selection by iteratively selecting variables that are highly correlated with the output variables, but which are not correlated with the previously chosen variables. To measure the correlation, our method uses the concept of projection operators and their algebra. With the projection operators the relationship, correlation, between sets of input and output variables can also be expressed by kernel functions, thus nonlinear correlation models can be exploited as well. We experimentally validate our approach, showing on both synthetic and real data its scalability and the relevance of the selected features. Keywords: Supervised variable selection, vector-valued learning, projection-valued measure, reproducing kernel Hilbert space

Vector-Valued Least-Squares Regression under Output Regularity Assumptions

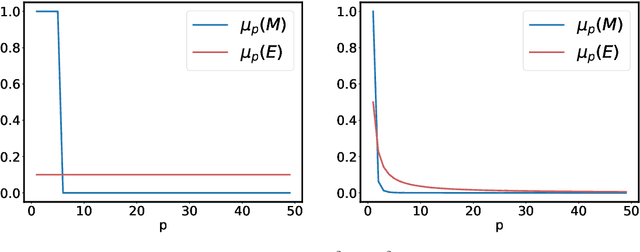
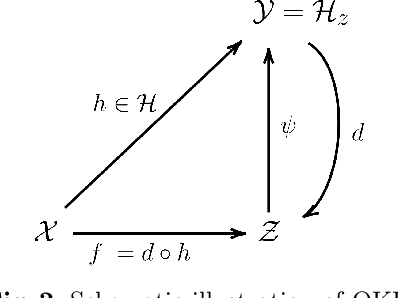
We propose and analyse a reduced-rank method for solving least-squares regression problems with infinite dimensional output. We derive learning bounds for our method, and study under which setting statistical performance is improved in comparison to full-rank method. Our analysis extends the interest of reduced-rank regression beyond the standard low-rank setting to more general output regularity assumptions. We illustrate our theoretical insights on synthetic least-squares problems. Then, we propose a surrogate structured prediction method derived from this reduced-rank method. We assess its benefits on three different problems: image reconstruction, multi-label classification, and metabolite identification.

Learning to Predict Graphs with Fused Gromov-Wasserstein Barycenters

This paper introduces a novel and generic framework to solve the flagship task of supervised labeled graph prediction by leveraging Optimal Transport tools. We formulate the problem as regression with the Fused Gromov-Wasserstein (FGW) loss and propose a predictive model relying on a FGW barycenter whose weights depend on inputs. First we introduce a non-parametric estimator based on kernel ridge regression for which theoretical results such as consistency and excess risk bound are proved. Next we propose an interpretable parametric model where the barycenter weights are modeled with a neural network and the graphs on which the FGW barycenter is calculated are additionally learned. Numerical experiments show the strength of the method and its ability to interpolate in the labeled graph space on simulated data and on a difficult metabolic identification problem where it can reach very good performance with very little engineering.

Learning primal-dual sparse kernel machines

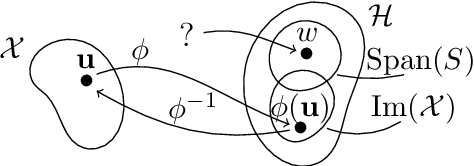
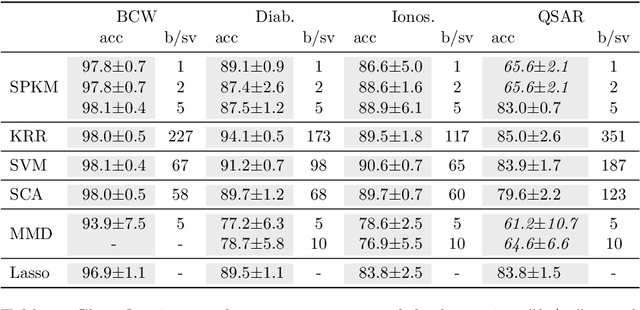
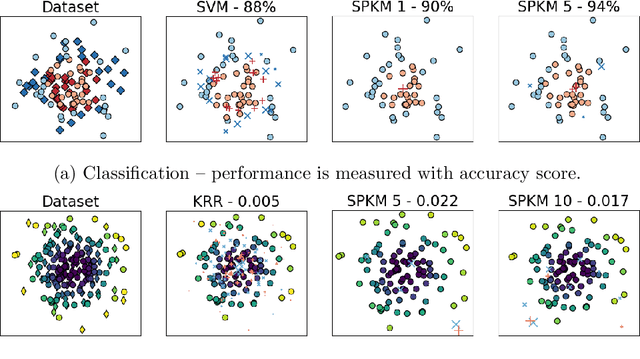
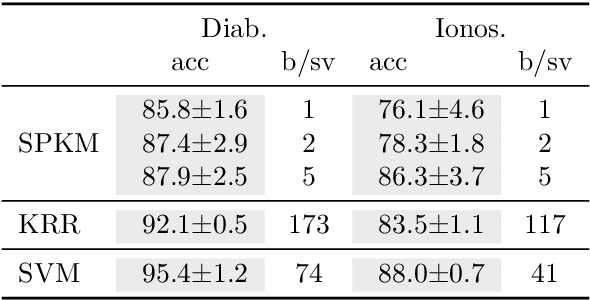
Traditionally, kernel methods rely on the representer theorem which states that the solution to a learning problem is obtained as a linear combination of the data mapped into the reproducing kernel Hilbert space (RKHS). While elegant from theoretical point of view, the theorem is prohibitive for algorithms' scalability to large datasets, and the interpretability of the learned function. In this paper, instead of using the traditional representer theorem, we propose to search for a solution in RKHS that has a pre-image decomposition in the original data space, where the elements don't necessarily correspond to the elements in the training set. Our gradient-based optimisation method then hinges on optimising over possibly sparse elements in the input space, and enables us to obtain a kernel-based model with both primal and dual sparsity. We give theoretical justification on the proposed method's generalization ability via a Rademacher bound. Our experiments demonstrate a better scalability and interpretability with accuracy on par with the traditional kernel-based models.

Learning Output Embeddings in Structured Prediction

A powerful and flexible approach to structured prediction consists in embedding the structured objects to be predicted into a feature space of possibly infinite dimension, and then, solving a regression problem in this output space. A prediction in the original space is computed by solving a pre-image problem. In such an approach, the embedding, linked to the target loss, is defined prior to the learning phase. In this work, we propose to jointly learn an approximation of the output embedding and the regression function into the new feature space. Output Embedding Learning (OEL) allows to leverage a priori information on the outputs and also unexploited unsupervised output data, which are both often available in structured prediction problems. We give a general learning method that we theoretically study in the linear case, proving consistency and excess-risk bound. OEL is tested on various structured prediction problems, showing its versatility and reveals to be especially useful when the training dataset is small compared to the complexity of the task.

A Solution for Large Scale Nonlinear Regression with High Rank and Degree at Constant Memory Complexity via Latent Tensor Reconstruction

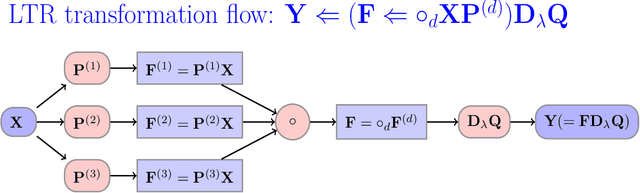
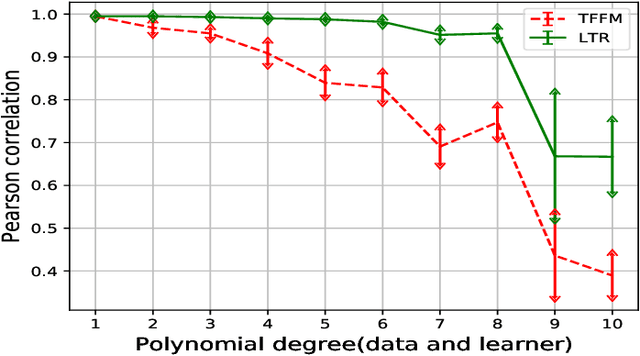
This paper proposes a novel method for learning highly nonlinear, multivariate functions from examples. Our method takes advantage of the property that continuous functions can be approximated by polynomials, which in turn are representable by tensors. Hence the function learning problem is transformed into a tensor reconstruction problem, an inverse problem of the tensor decomposition. Our method incrementally builds up the unknown tensor from rank-one terms, which lets us control the complexity of the learned model and reduce the chance of overfitting. For learning the models, we present an efficient gradient-based algorithm that can be implemented in linear time in the sample size, order, rank of the tensor and the dimension of the input. In addition to regression, we present extensions to classification, multi-view learning and vector-valued output as well as a multi-layered formulation. The method can work in an online fashion via processing mini-batches of the data with constant memory complexity. Consequently, it can fit into systems equipped only with limited resources such as embedded systems or mobile phones. Our experiments demonstrate a favorable accuracy and running time compared to competing methods.

Bayesian Metabolic Flux Analysis reveals intracellular flux couplings

Metabolic flux balance analyses are a standard tool in analysing metabolic reaction rates compatible with measurements, steady-state and the metabolic reaction network stoichiometry. Flux analysis methods commonly place unrealistic assumptions on fluxes due to the convenience of formulating the problem as a linear programming model, and most methods ignore the notable uncertainty in flux estimates. We introduce a novel paradigm of Bayesian metabolic flux analysis that models the reactions of the whole genome-scale cellular system in probabilistic terms, and can infer the full flux vector distribution of genome-scale metabolic systems based on exchange and intracellular (e.g. 13C) flux measurements, steady-state assumptions, and target function assumptions. The Bayesian model couples all fluxes jointly together in a simple truncated multivariate posterior distribution, which reveals informative flux couplings. Our model is a plug-in replacement to conventional metabolic balance methods, such as flux balance analysis (FBA). Our experiments indicate that we can characterise the genome-scale flux covariances, reveal flux couplings, and determine more intracellular unobserved fluxes in C. acetobutylicum from 13C data than flux variability analysis. The COBRA compatible software is available at github.com/markusheinonen/bamfa

A Tutorial on Canonical Correlation Methods

Canonical correlation analysis is a family of multivariate statistical methods for the analysis of paired sets of variables. Since its proposition, canonical correlation analysis has for instance been extended to extract relations between two sets of variables when the sample size is insufficient in relation to the data dimensionality, when the relations have been considered to be non-linear, and when the dimensionality is too large for human interpretation. This tutorial explains the theory of canonical correlation analysis including its regularised, kernel, and sparse variants. Additionally, the deep and Bayesian CCA extensions are briefly reviewed. Together with the numerical examples, this overview provides a coherent compendium on the applicability of the variants of canonical correlation analysis. By bringing together techniques for solving the optimisation problems, evaluating the statistical significance and generalisability of the canonical correlation model, and interpreting the relations, we hope that this article can serve as a hands-on tool for applying canonical correlation methods in data analysis.