Scalable variable selection for two-view learning tasks with projection operators

In this paper we propose a novel variable selection method for two-view settings, or for vector-valued supervised learning problems. Our framework is able to handle extremely large scale selection tasks, where number of data samples could be even millions. In a nutshell, our method performs variable selection by iteratively selecting variables that are highly correlated with the output variables, but which are not correlated with the previously chosen variables. To measure the correlation, our method uses the concept of projection operators and their algebra. With the projection operators the relationship, correlation, between sets of input and output variables can also be expressed by kernel functions, thus nonlinear correlation models can be exploited as well. We experimentally validate our approach, showing on both synthetic and real data its scalability and the relevance of the selected features. Keywords: Supervised variable selection, vector-valued learning, projection-valued measure, reproducing kernel Hilbert space

Learning primal-dual sparse kernel machines

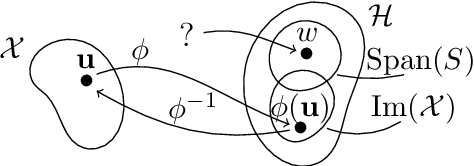
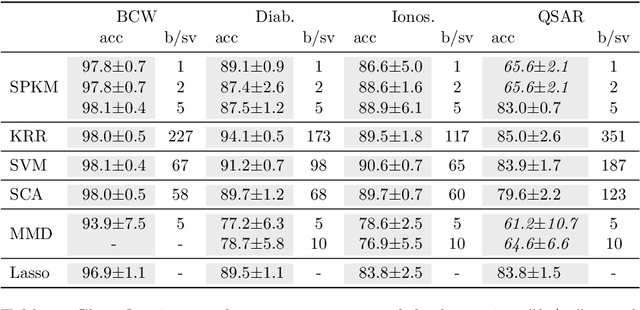
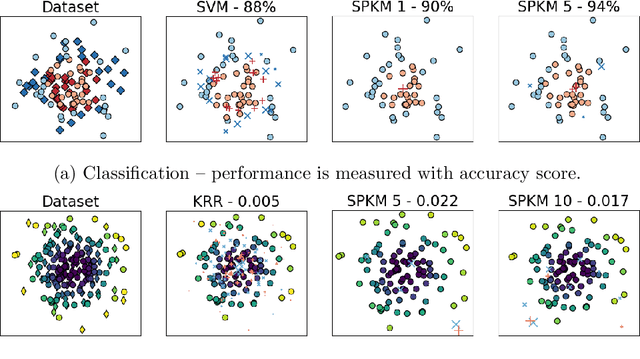
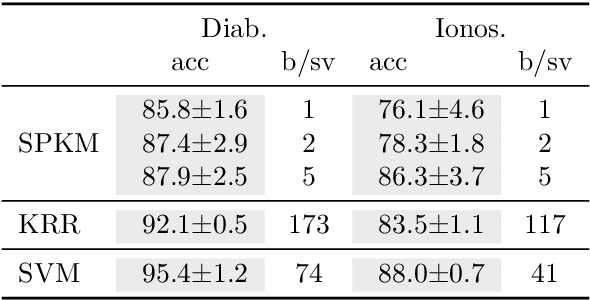
Traditionally, kernel methods rely on the representer theorem which states that the solution to a learning problem is obtained as a linear combination of the data mapped into the reproducing kernel Hilbert space (RKHS). While elegant from theoretical point of view, the theorem is prohibitive for algorithms' scalability to large datasets, and the interpretability of the learned function. In this paper, instead of using the traditional representer theorem, we propose to search for a solution in RKHS that has a pre-image decomposition in the original data space, where the elements don't necessarily correspond to the elements in the training set. Our gradient-based optimisation method then hinges on optimising over possibly sparse elements in the input space, and enables us to obtain a kernel-based model with both primal and dual sparsity. We give theoretical justification on the proposed method's generalization ability via a Rademacher bound. Our experiments demonstrate a better scalability and interpretability with accuracy on par with the traditional kernel-based models.

Entangled Kernels -- Beyond Separability

We consider the problem of operator-valued kernel learning and investigate the possibility of going beyond the well-known separable kernels. Borrowing tools and concepts from the field of quantum computing, such as partial trace and entanglement, we propose a new view on operator-valued kernels and define a general family of kernels that encompasses previously known operator-valued kernels, including separable and transformable kernels. Within this framework, we introduce another novel class of operator-valued kernels called entangled kernels that are not separable. We propose an efficient two-step algorithm for this framework, where the entangled kernel is learned based on a novel extension of kernel alignment to operator-valued kernels. We illustrate our algorithm with an application to supervised dimensionality reduction, and demonstrate its effectiveness with both artificial and real data for multi-output regression.

Partial Trace Regression and Low-Rank Kraus Decomposition

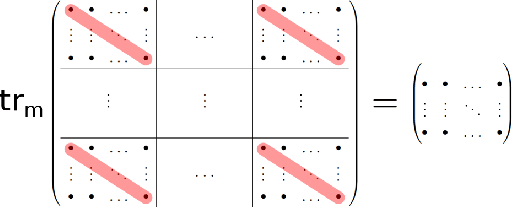
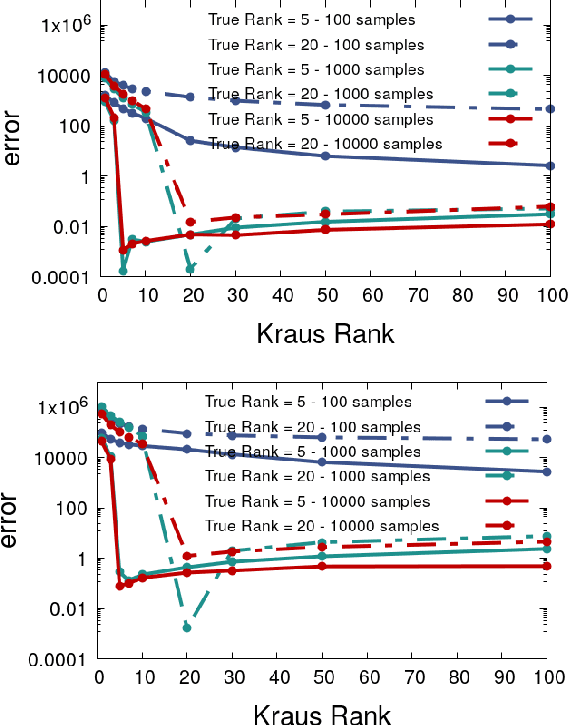
The trace regression model, a direct extension of the well-studied linear regression model, allows one to map matrices to real-valued outputs. We here introduce an even more general model, namely the partial-trace regression model, a family of linear mappings from matrix-valued inputs to matrix-valued outputs; this model subsumes the trace regression model and thus the linear regression model. Borrowing tools from quantum information theory, where partial trace operators have been extensively studied, we propose a framework for learning partial trace regression models from data by taking advantage of the so-called low-rank Kraus representation of completely positive maps. We show the relevance of our framework with synthetic and real-world experiments conducted for both i) matrix-to-matrix regression and ii) positive semidefinite matrix completion, two tasks which can be formulated as partial trace regression problems.

Kernel transfer over multiple views for missing data completion

We consider the kernel completion problem with the presence of multiple views in the data. In this context the data samples can be fully missing in some views, creating missing columns and rows to the kernel matrices that are calculated individually for each view. We propose to solve the problem of completing the kernel matrices by transferring the features of the other views to represent the view under consideration. We align the known part of the kernel matrix with a new kernel built from the features of the other views. We are thus able to find generalizable structures in the kernel under completion, and represent it accurately. Its missing values can be predicted with the data available in other views. We illustrate the benefits of our approach with simulated data and multivariate digits dataset, as well as with real biological datasets from studies of pattern formation in early \textit{Drosophila melanogaster} embryogenesis.

Multi-view Metric Learning in Vector-valued Kernel Spaces

We consider the problem of metric learning for multi-view data and present a novel method for learning within-view as well as between-view metrics in vector-valued kernel spaces, as a way to capture multi-modal structure of the data. We formulate two convex optimization problems to jointly learn the metric and the classifier or regressor in kernel feature spaces. An iterative three-step multi-view metric learning algorithm is derived from the optimization problems. In order to scale the computation to large training sets, a block-wise Nystr{\"o}m approximation of the multi-view kernel matrix is introduced. We justify our approach theoretically and experimentally, and show its performance on real-world datasets against relevant state-of-the-art methods.