Variational Boosted Soft Trees

Gradient boosting machines (GBMs) based on decision trees consistently demonstrate state-of-the-art results on regression and classification tasks with tabular data, often outperforming deep neural networks. However, these models do not provide well-calibrated predictive uncertainties, which prevents their use for decision making in high-risk applications. The Bayesian treatment is known to improve predictive uncertainty calibration, but previously proposed Bayesian GBM methods are either computationally expensive, or resort to crude approximations. Variational inference is often used to implement Bayesian neural networks, but is difficult to apply to GBMs, because the decision trees used as weak learners are non-differentiable. In this paper, we propose to implement Bayesian GBMs using variational inference with soft decision trees, a fully differentiable alternative to standard decision trees introduced by Irsoy et al. Our experiments demonstrate that variational soft trees and variational soft GBMs provide useful uncertainty estimates, while retaining good predictive performance. The proposed models show higher test likelihoods when compared to the state-of-the-art Bayesian GBMs in 7/10 tabular regression datasets and improved out-of-distribution detection in 5/10 datasets.

Bayesian Nonparametric Boolean Factor Models

We build upon probabilistic models for Boolean Matrix and Boolean Tensor factorisation that have recently been shown to solve these problems with unprecedented accuracy and to enable posterior inference to scale to Billions of observation. Here, we lift the restriction of a pre-specified number of latent dimensions by introducing an Indian Buffet Process prior over factor matrices. Not only does the full factor-conditional take a computationally convenient form due to the logical dependencies in the model, but also the posterior over the number of non-zero latent dimensions is remarkably simple. It amounts to counting the number false and true negative predictions, whereas positive predictions can be ignored. This constitutes a very transparent example of sampling-based posterior inference with an IBP prior and, importantly, lets us maintain extremely efficient inference. We discuss applications to simulated data, as well as to a real world data matrix with 6 Million entries.

TensOrMachine: Probabilistic Boolean Tensor Decomposition

Boolean tensor decomposition approximates data of multi-way binary relationships as product of interpretable low-rank binary factors, following the rules of Boolean algebra. Here, we present its first probabilistic treatment. We facilitate scalable sampling-based posterior inference by exploitation of the combinatorial structure of the factor conditionals. Maximum a posteriori decompositions feature higher accuracies than existing techniques throughout a wide range of simulated conditions. Moreover, the probabilistic approach facilitates the treatment of missing data and enables model selection with much greater accuracy. We investigate three real-world data-sets. First, temporal interaction networks in a hospital ward and behavioural data of university students demonstrate the inference of instructive latent patterns. Next, we decompose a tensor with more than 10 billion data points, indicating relations of gene expression in cancer patients. Not only does this demonstrate scalability, it also provides an entirely novel perspective on relational properties of continuous data and, in the present example, on the molecular heterogeneity of cancer. Our implementation is available on GitHub: https://github.com/TammoR/LogicalFactorisationMachines.

An interpretable latent variable model for attribute applicability in the Amazon catalogue

Learning attribute applicability of products in the Amazon catalog (e.g., predicting that a shoe should have a value for size, but not for battery-type at scale is a challenge. The need for an interpretable model is contingent on (1) the lack of ground truth training data, (2) the need to utilise prior information about the underlying latent space and (3) the ability to understand the quality of predictions on new, unseen data. To this end, we develop the MaxMachine, a probabilistic latent variable model that learns distributed binary representations, associated to sets of features that are likely to co-occur in the data. Layers of MaxMachines can be stacked such that higher layers encode more abstract information. Any set of variables can be clamped to encode prior information. We develop fast sampling based posterior inference. Preliminary results show that the model improves over the baseline in 17 out of 19 product groups and provides qualitatively reasonable predictions.

Bayesian Boolean Matrix Factorisation

Boolean matrix factorisation aims to decompose a binary data matrix into an approximate Boolean product of two low rank, binary matrices: one containing meaningful patterns, the other quantifying how the observations can be expressed as a combination of these patterns. We introduce the OrMachine, a probabilistic generative model for Boolean matrix factorisation and derive a Metropolised Gibbs sampler that facilitates efficient parallel posterior inference. On real world and simulated data, our method outperforms all currently existing approaches for Boolean matrix factorisation and completion. This is the first method to provide full posterior inference for Boolean Matrix factorisation which is relevant in applications, e.g. for controlling false positive rates in collaborative filtering and, crucially, improves the interpretability of the inferred patterns. The proposed algorithm scales to large datasets as we demonstrate by analysing single cell gene expression data in 1.3 million mouse brain cells across 11 thousand genes on commodity hardware.

Resting state brain networks from EEG: Hidden Markov states vs. classical microstates

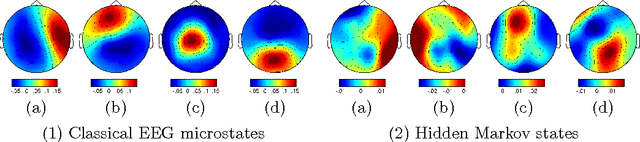
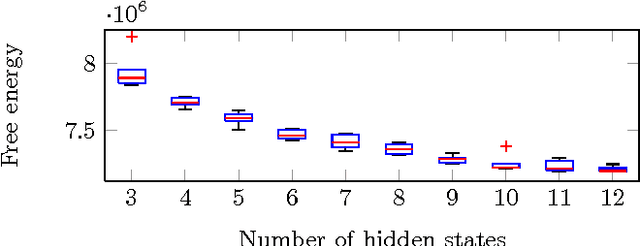
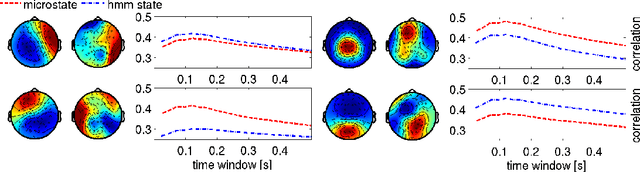
Functional brain networks exhibit dynamics on the sub-second temporal scale and are often assumed to embody the physiological substrate of cognitive processes. Here we analyse the temporal and spatial dynamics of these states, as measured by EEG, with a hidden Markov model and compare this approach to classical EEG microstate analysis. We find dominating state lifetimes of 100--150\,ms for both approaches. The state topographies show obvious similarities. However, they also feature distinct spatial and especially temporal properties. These differences may carry physiological meaningful information originating from patterns in the data that the HMM is able to integrate while the microstate analysis is not. This hypothesis is supported by a consistently high pairwise correlation of the temporal evolution of EEG microstates which is not observed for the HMM states and which seems unlikely to be a good description of the underlying physiology. However, further investigation is required to determine the robustness and the functional and clinical relevance of EEG HMM states in comparison to EEG microstates.