The 2025 PNPL Competition: Speech Detection and Phoneme Classification in the LibriBrain Dataset

The advance of speech decoding from non-invasive brain data holds the potential for profound societal impact. Among its most promising applications is the restoration of communication to paralysed individuals affected by speech deficits such as dysarthria, without the need for high-risk surgical interventions. The ultimate aim of the 2025 PNPL competition is to produce the conditions for an "ImageNet moment" or breakthrough in non-invasive neural decoding, by harnessing the collective power of the machine learning community. To facilitate this vision we present the largest within-subject MEG dataset recorded to date (LibriBrain) together with a user-friendly Python library (pnpl) for easy data access and integration with deep learning frameworks. For the competition we define two foundational tasks (i.e. Speech Detection and Phoneme Classification from brain data), complete with standardised data splits and evaluation metrics, illustrative benchmark models, online tutorial code, a community discussion board, and public leaderboard for submissions. To promote accessibility and participation the competition features a Standard track that emphasises algorithmic innovation, as well as an Extended track that is expected to reward larger-scale computing, accelerating progress toward a non-invasive brain-computer interface for speech.

The Brain's Bitter Lesson: Scaling Speech Decoding With Self-Supervised Learning

The past few years have produced a series of spectacular advances in the decoding of speech from brain activity. The engine of these advances has been the acquisition of labelled data, with increasingly large datasets acquired from single subjects. However, participants exhibit anatomical and other individual differences, and datasets use varied scanners and task designs. As a result, prior work has struggled to leverage data from multiple subjects, multiple datasets, multiple tasks, and unlabelled datasets. In turn, the field has not benefited from the rapidly growing number of open neural data repositories to exploit large-scale data and deep learning. To address this, we develop an initial set of neuroscience-inspired self-supervised objectives, together with a neural architecture, for representation learning from heterogeneous and unlabelled neural recordings. Experimental results show that representations learned with these objectives generalise across subjects, datasets, and tasks, and are also learned faster than using only labelled data. In addition, we set new benchmarks for two foundational speech decoding tasks. Taken together, these methods now unlock the potential for training speech decoding models with orders of magnitude more existing data.

Foundational GPT Model for MEG

Deep learning techniques can be used to first training unsupervised models on large amounts of unlabelled data, before fine-tuning the models on specific tasks. This approach has seen massive success for various kinds of data, e.g. images, language, audio, and holds the promise of improving performance in various downstream tasks (e.g. encoding or decoding brain data). However, there has been limited progress taking this approach for modelling brain signals, such as Magneto-/electroencephalography (M/EEG). Here we propose two classes of deep learning foundational models that can be trained using forecasting of unlabelled MEG. First, we consider a modified Wavenet; and second, we consider a modified Transformer-based (GPT2) model. The modified GPT2 includes a novel application of tokenisation and embedding methods, allowing a model developed initially for the discrete domain of language to be applied to continuous multichannel time series data. We also extend the forecasting framework to include condition labels as inputs, enabling better modelling (encoding) of task data. We compare the performance of these deep learning models with standard linear autoregressive (AR) modelling on MEG data. This shows that GPT2-based models provide better modelling capabilities than Wavenet and linear AR models, by better reproducing the temporal, spatial and spectral characteristics of real data and evoked activity in task data. We show how the GPT2 model scales well to multiple subjects, while adapting its model to each subject through subject embedding. Finally, we show how such a model can be useful in downstream decoding tasks through data simulation. All code is available on GitHub (https://github.com/ricsinaruto/MEG-transfer-decoding).

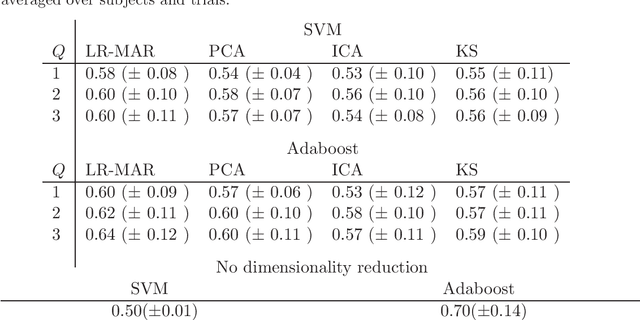
Generalizing Brain Decoding Across Subjects with Deep Learning

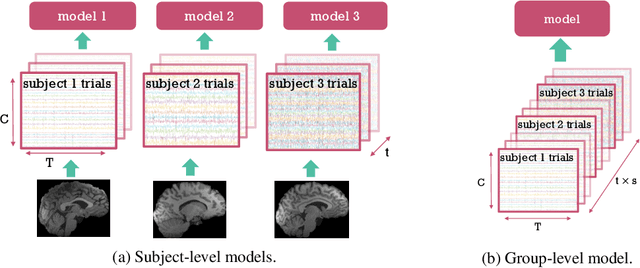
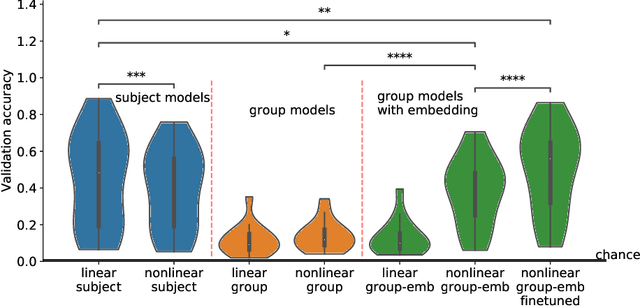
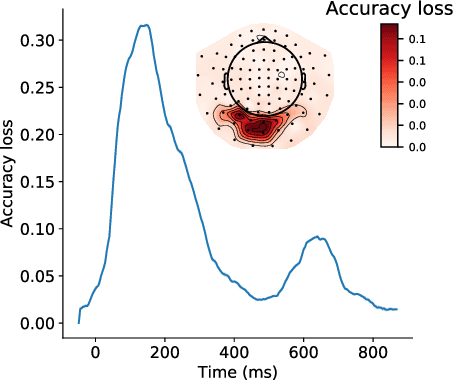
Decoding experimental variables from brain imaging data is gaining popularity, with applications in brain-computer interfaces and the study of neural representations. Decoding is typically subject-specific and does not generalise well over subjects. Here, we investigate ways to achieve cross-subject decoding. We used magnetoencephalography (MEG) data where 15 subjects viewed 118 different images, with 30 examples per image. Training on the entire 1s window following the presentation of each image, we experimented with an adaptation of the WaveNet architecture for classification. We also investigated the use of subject embedding to aid learning of subject variability in the group model. We show that deep learning and subject embedding are crucial to closing the performance gap between subject and group-level models. Importantly group models outperform subject models when tested on an unseen subject with little available data. The potential of such group modelling is even higher with bigger datasets. Furthermore, we demonstrate the use of permutation feature importance to gain insight into the spatio-temporal and spectral information encoded in the models, enabling better physiological interpretation. All experimental code is available at https://github.com/ricsinaruto/MEG-group-decode.

Resting state brain networks from EEG: Hidden Markov states vs. classical microstates

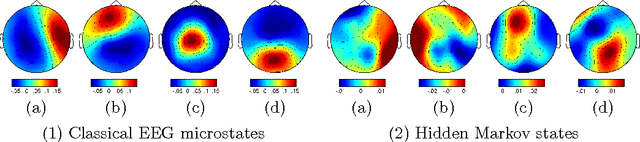
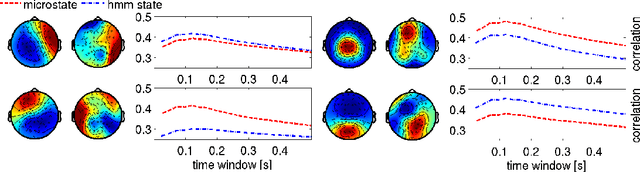
Functional brain networks exhibit dynamics on the sub-second temporal scale and are often assumed to embody the physiological substrate of cognitive processes. Here we analyse the temporal and spatial dynamics of these states, as measured by EEG, with a hidden Markov model and compare this approach to classical EEG microstate analysis. We find dominating state lifetimes of 100--150\,ms for both approaches. The state topographies show obvious similarities. However, they also feature distinct spatial and especially temporal properties. These differences may carry physiological meaningful information originating from patterns in the data that the HMM is able to integrate while the microstate analysis is not. This hypothesis is supported by a consistently high pairwise correlation of the temporal evolution of EEG microstates which is not observed for the HMM states and which seems unlikely to be a good description of the underlying physiology. However, further investigation is required to determine the robustness and the functional and clinical relevance of EEG HMM states in comparison to EEG microstates.

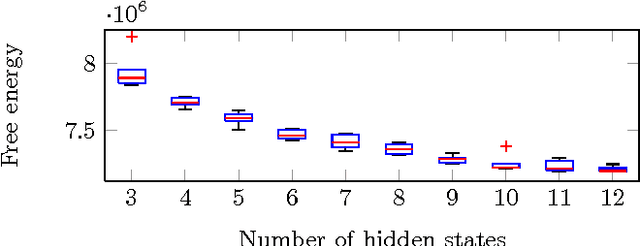
Dimensionality reduction for time series data

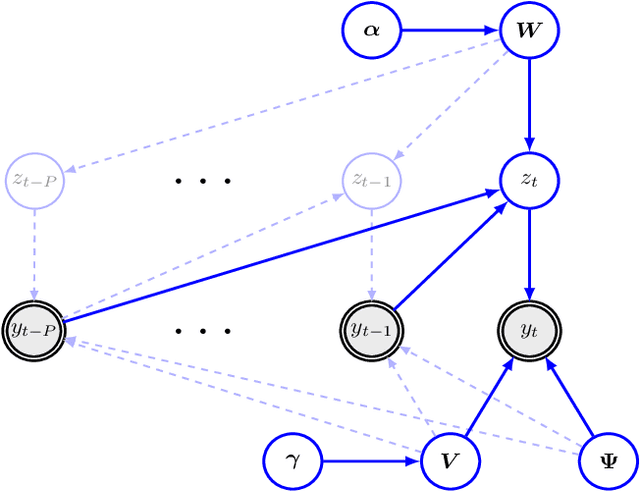
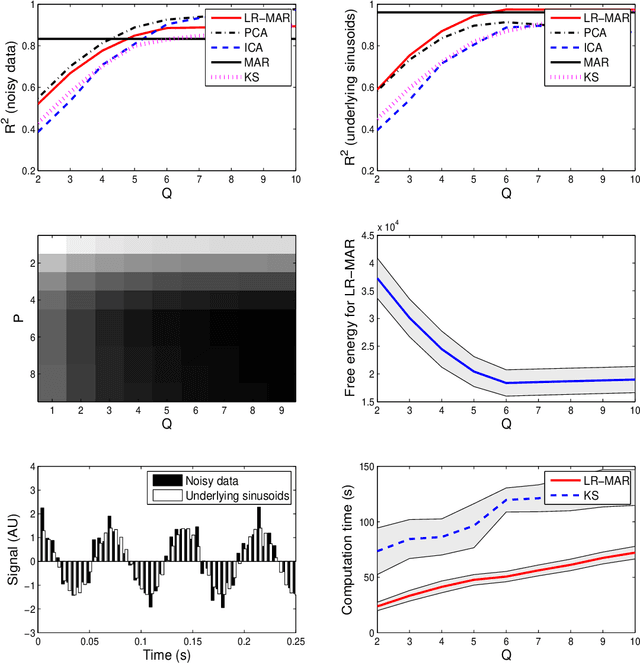
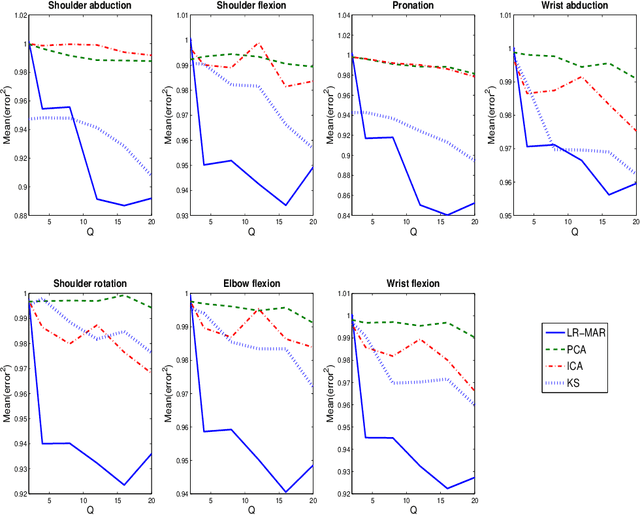
Despite the fact that they do not consider the temporal nature of data, classic dimensionality reduction techniques, such as PCA, are widely applied to time series data. In this paper, we introduce a factor decomposition specific for time series that builds upon the Bayesian multivariate autoregressive model and hence evades the assumption that data points are mutually independent. The key is to find a low-rank estimation of the autoregressive matrices. As in the probabilistic version of other factor models, this induces a latent low-dimensional representation of the original data. We discuss some possible generalisations and alternatives, with the most relevant being a technique for simultaneous smoothing and dimensionality reduction. To illustrate the potential applications, we apply the model on a synthetic data set and different types of neuroimaging data (EEG and ECoG).