Dimensionality reduction for time series data

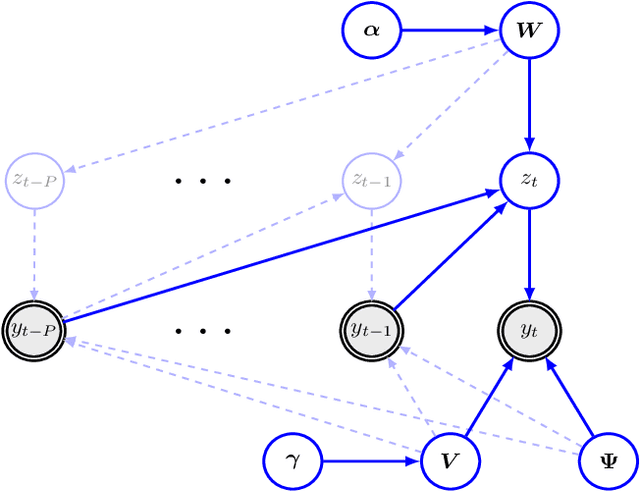
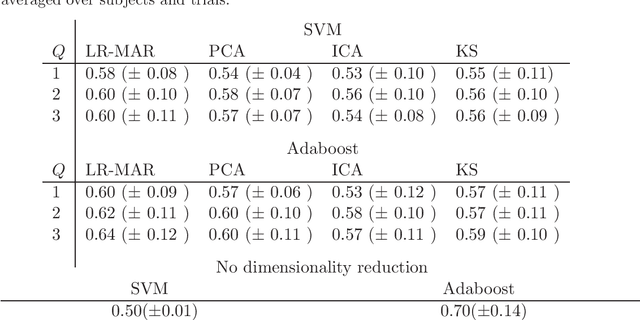
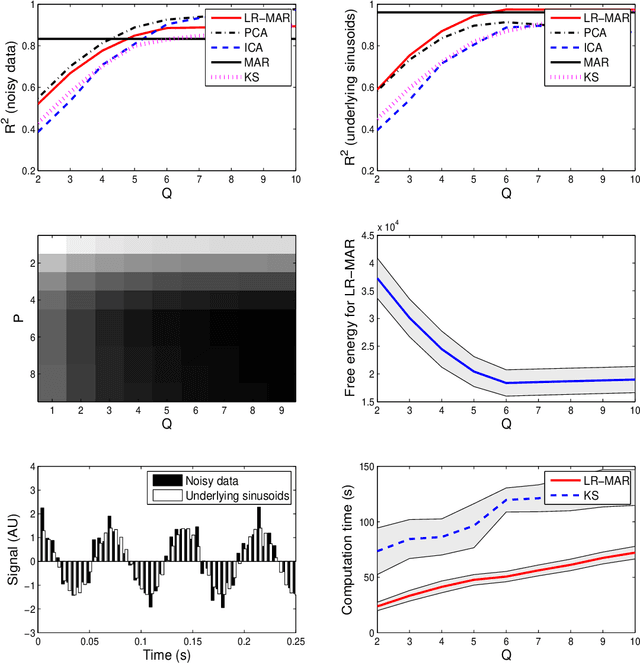
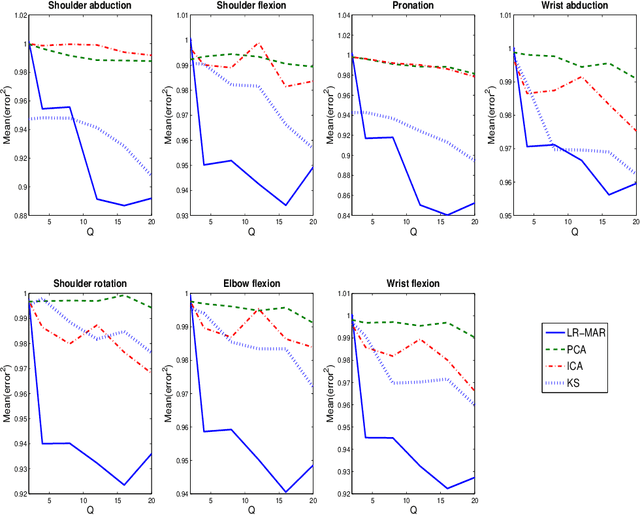
Despite the fact that they do not consider the temporal nature of data, classic dimensionality reduction techniques, such as PCA, are widely applied to time series data. In this paper, we introduce a factor decomposition specific for time series that builds upon the Bayesian multivariate autoregressive model and hence evades the assumption that data points are mutually independent. The key is to find a low-rank estimation of the autoregressive matrices. As in the probabilistic version of other factor models, this induces a latent low-dimensional representation of the original data. We discuss some possible generalisations and alternatives, with the most relevant being a technique for simultaneous smoothing and dimensionality reduction. To illustrate the potential applications, we apply the model on a synthetic data set and different types of neuroimaging data (EEG and ECoG).

Bayesian one-mode projection for dynamic bipartite graphs

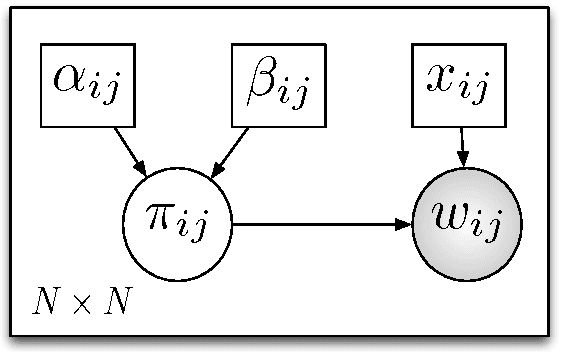
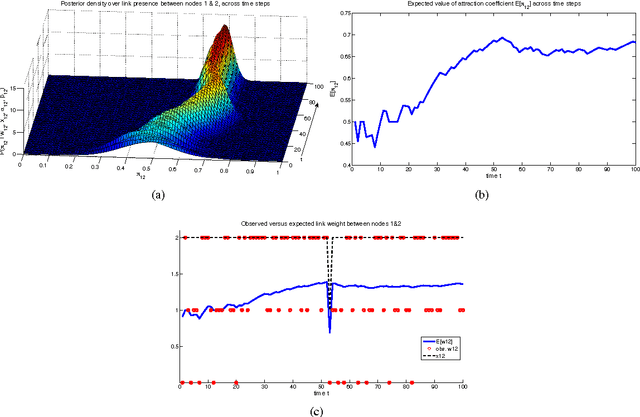
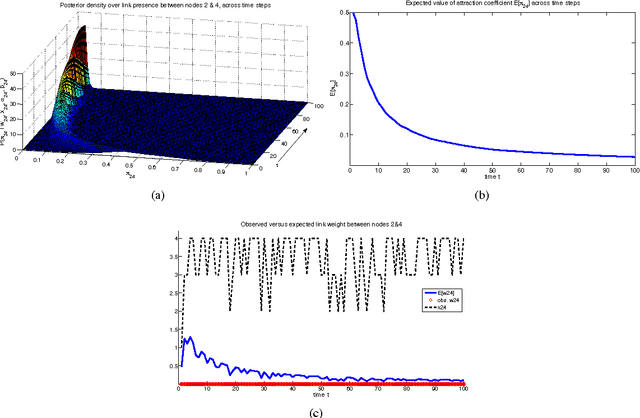
We propose a Bayesian methodology for one-mode projecting a bipartite network that is being observed across a series of discrete time steps. The resulting one mode network captures the uncertainty over the presence/absence of each link and provides a probability distribution over its possible weight values. Additionally, the incorporation of prior knowledge over previous states makes the resulting network less sensitive to noise and missing observations that usually take place during the data collection process. The methodology consists of computationally inexpensive update rules and is scalable to large problems, via an appropriate distributed implementation.

Models of Disease Spectra

Case vs control comparisons have been the classical approach to the study of neurological diseases. However, most patients will not fall cleanly into either group. Instead, clinicians will typically find patients that cannot be classified as having clearly progressed into the disease state. For those subjects, very little can be said about their brain function on the basis of analyses of group differences. To describe the intermediate brain function requires models that interpolate between the disease states. We have chosen Gaussian Processes (GP) regression to obtain a continuous spectrum of brain activation and to extract the unknown disease progression profile. Our models incorporate spatial distribution of measures of activation, e.g. the correlation of an fMRI trace with an input stimulus, and so constitute ultra-high multi-variate GP regressors. We applied GPs to model fMRI image phenotypes across Alzheimer's Disease (AD) behavioural measures, e.g. MMSE, ACE etc. scores, and obtained predictions at non-observed MMSE/ACE values. The overall model confirmed the known reduction in the spatial extent of activity in response to reading versus false-font stimulation. The predictive uncertainty indicated the worsening confidence intervals at behavioural scores distance from those used for GP training. Thus, the model indicated the type of patient (what behavioural score) that would need to included in the training data to improve models predictions.

Constrained Mixture Models for Asset Returns Modelling

The estimation of asset return distributions is crucial for determining optimal trading strategies. In this paper we describe the constrained mixture model, based on a mixture of Gamma and Gaussian distributions, to provide an accurate description of price trends as being clearly positive, negative or ranging while accounting for heavy tails and high kurtosis. The model is estimated in the Expectation Maximisation framework and model order estimation also respects the model's constraints.