The Gaussian-Linear Hidden Markov model: a Python package

We propose the Gaussian-Linear Hidden Markov model (GLHMM), a generalisation of different types of HMMs commonly used in neuroscience. In short, the GLHMM is a general framework where linear regression is used to flexibly parameterise the Gaussian state distribution, thereby accommodating a wide range of uses -including unsupervised, encoding and decoding models. GLHMM is implemented as a Python toolbox with an emphasis on statistical testing and out-of-sample prediction -i.e. aimed at finding and characterising brain-behaviour associations. The toolbox uses a stochastic variational inference approach, enabling it to handle large data sets at reasonable computational time. Overall, the approach can be applied to several data modalities, including animal recordings or non-brain data, and applied over a broad range of experimental paradigms. For demonstration, we show examples with fMRI, electrocorticography, magnetoencephalo-graphy and pupillometry.

Dimensionality reduction for time series data

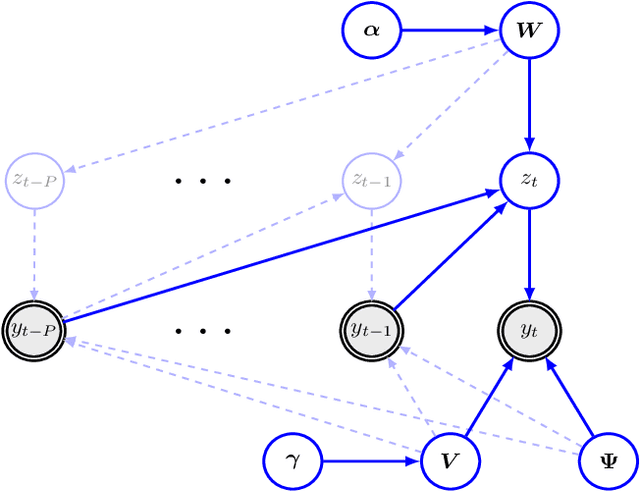
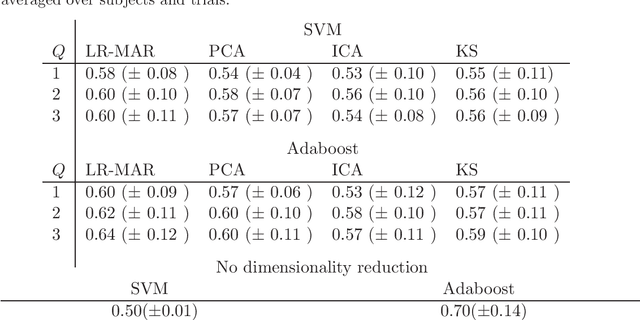
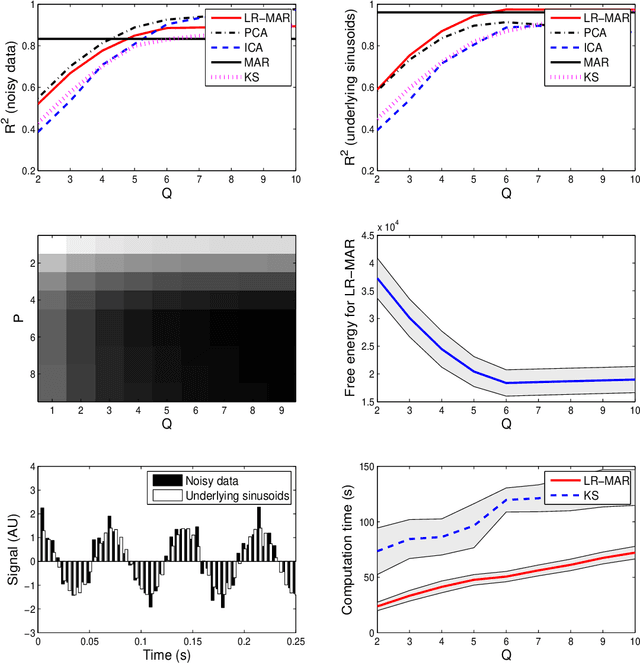
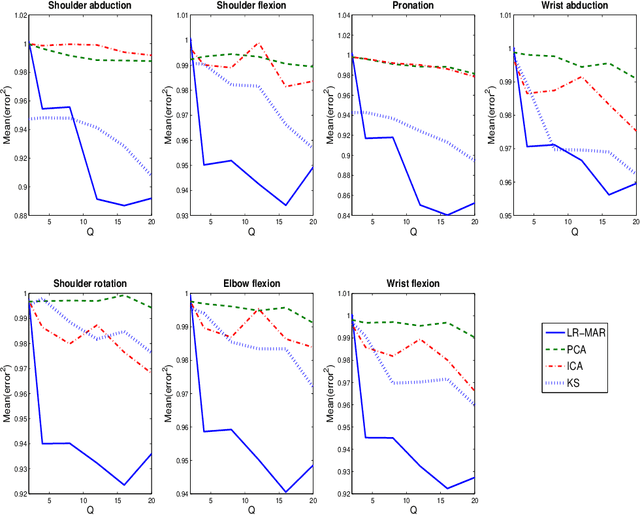
Despite the fact that they do not consider the temporal nature of data, classic dimensionality reduction techniques, such as PCA, are widely applied to time series data. In this paper, we introduce a factor decomposition specific for time series that builds upon the Bayesian multivariate autoregressive model and hence evades the assumption that data points are mutually independent. The key is to find a low-rank estimation of the autoregressive matrices. As in the probabilistic version of other factor models, this induces a latent low-dimensional representation of the original data. We discuss some possible generalisations and alternatives, with the most relevant being a technique for simultaneous smoothing and dimensionality reduction. To illustrate the potential applications, we apply the model on a synthetic data set and different types of neuroimaging data (EEG and ECoG).