Samuel L. Harrison
Dimensionality reduction for time series data
Jun 14, 2014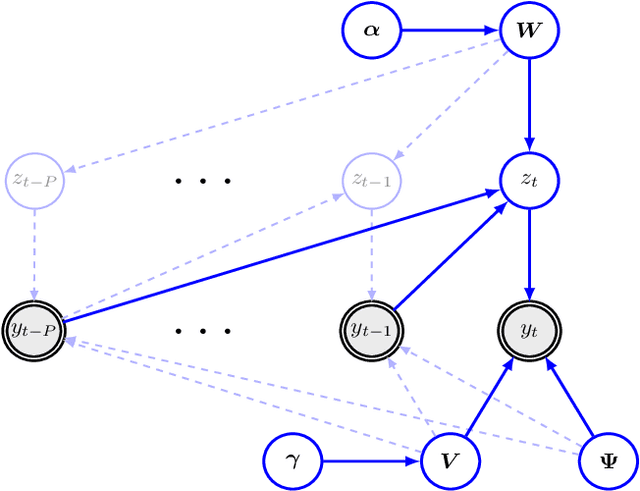
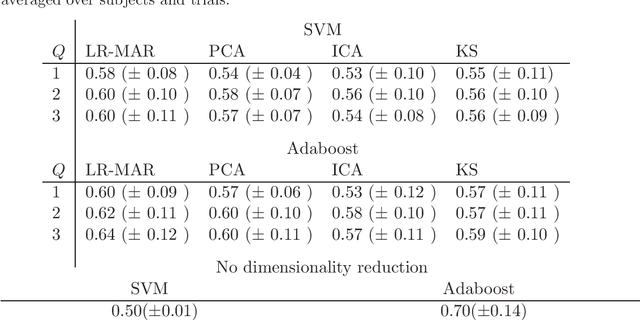
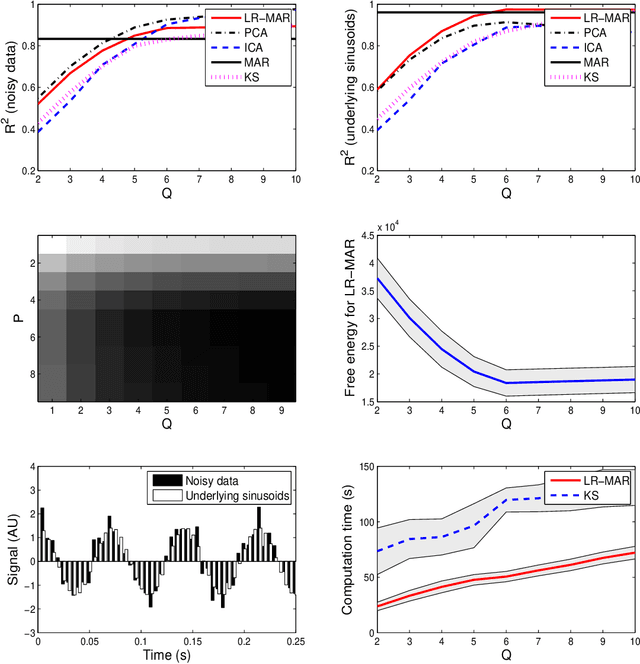
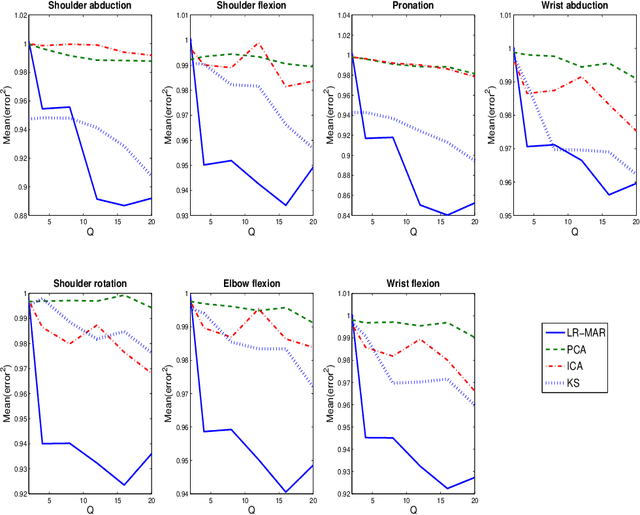
Abstract:Despite the fact that they do not consider the temporal nature of data, classic dimensionality reduction techniques, such as PCA, are widely applied to time series data. In this paper, we introduce a factor decomposition specific for time series that builds upon the Bayesian multivariate autoregressive model and hence evades the assumption that data points are mutually independent. The key is to find a low-rank estimation of the autoregressive matrices. As in the probabilistic version of other factor models, this induces a latent low-dimensional representation of the original data. We discuss some possible generalisations and alternatives, with the most relevant being a technique for simultaneous smoothing and dimensionality reduction. To illustrate the potential applications, we apply the model on a synthetic data set and different types of neuroimaging data (EEG and ECoG).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge