Score-Optimal Diffusion Schedules

Denoising diffusion models (DDMs) offer a flexible framework for sampling from high dimensional data distributions. DDMs generate a path of probability distributions interpolating between a reference Gaussian distribution and a data distribution by incrementally injecting noise into the data. To numerically simulate the sampling process, a discretisation schedule from the reference back towards clean data must be chosen. An appropriate discretisation schedule is crucial to obtain high quality samples. However, beyond hand crafted heuristics, a general method for choosing this schedule remains elusive. This paper presents a novel algorithm for adaptively selecting an optimal discretisation schedule with respect to a cost that we derive. Our cost measures the work done by the simulation procedure to transport samples from one point in the diffusion path to the next. Our method does not require hyperparameter tuning and adapts to the dynamics and geometry of the diffusion path. Our algorithm only involves the evaluation of the estimated Stein score, making it scalable to existing pre-trained models at inference time and online during training. We find that our learned schedule recovers performant schedules previously only discovered through manual search and obtains competitive FID scores on image datasets.

Approximations to the Fisher Information Metric of Deep Generative Models for Out-Of-Distribution Detection

Likelihood-based deep generative models such as score-based diffusion models and variational autoencoders are state-of-the-art machine learning models approximating high-dimensional distributions of data such as images, text, or audio. One of many downstream tasks they can be naturally applied to is out-of-distribution (OOD) detection. However, seminal work by Nalisnick et al. which we reproduce showed that deep generative models consistently infer higher log-likelihoods for OOD data than data they were trained on, marking an open problem. In this work, we analyse using the gradient of a data point with respect to the parameters of the deep generative model for OOD detection, based on the simple intuition that OOD data should have larger gradient norms than training data. We formalise measuring the size of the gradient as approximating the Fisher information metric. We show that the Fisher information matrix (FIM) has large absolute diagonal values, motivating the use of chi-square distributed, layer-wise gradient norms as features. We combine these features to make a simple, model-agnostic and hyperparameter-free method for OOD detection which estimates the joint density of the layer-wise gradient norms for a given data point. We find that these layer-wise gradient norms are weakly correlated, rendering their combined usage informative, and prove that the layer-wise gradient norms satisfy the principle of (data representation) invariance. Our empirical results indicate that this method outperforms the Typicality test for most deep generative models and image dataset pairings.

A Unified Framework for U-Net Design and Analysis

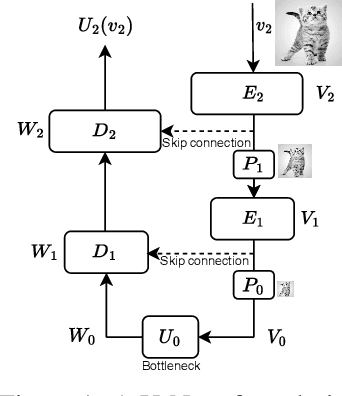
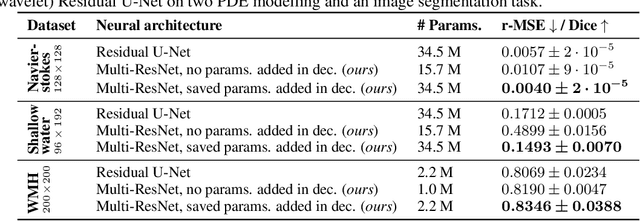
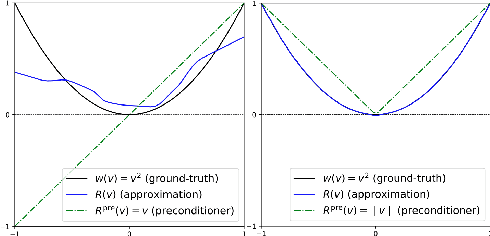
U-Nets are a go-to, state-of-the-art neural architecture across numerous tasks for continuous signals on a square such as images and Partial Differential Equations (PDE), however their design and architecture is understudied. In this paper, we provide a framework for designing and analysing general U-Net architectures. We present theoretical results which characterise the role of the encoder and decoder in a U-Net, their high-resolution scaling limits and their conjugacy to ResNets via preconditioning. We propose Multi-ResNets, U-Nets with a simplified, wavelet-based encoder without learnable parameters. Further, we show how to design novel U-Net architectures which encode function constraints, natural bases, or the geometry of the data. In diffusion models, our framework enables us to identify that high-frequency information is dominated by noise exponentially faster, and show how U-Nets with average pooling exploit this. In our experiments, we demonstrate how Multi-ResNets achieve competitive and often superior performance compared to classical U-Nets in image segmentation, PDE surrogate modelling, and generative modelling with diffusion models. Our U-Net framework paves the way to study the theoretical properties of U-Nets and design natural, scalable neural architectures for a multitude of problems beyond the square.

A Multi-Resolution Framework for U-Nets with Applications to Hierarchical VAEs

U-Net architectures are ubiquitous in state-of-the-art deep learning, however their regularisation properties and relationship to wavelets are understudied. In this paper, we formulate a multi-resolution framework which identifies U-Nets as finite-dimensional truncations of models on an infinite-dimensional function space. We provide theoretical results which prove that average pooling corresponds to projection within the space of square-integrable functions and show that U-Nets with average pooling implicitly learn a Haar wavelet basis representation of the data. We then leverage our framework to identify state-of-the-art hierarchical VAEs (HVAEs), which have a U-Net architecture, as a type of two-step forward Euler discretisation of multi-resolution diffusion processes which flow from a point mass, introducing sampling instabilities. We also demonstrate that HVAEs learn a representation of time which allows for improved parameter efficiency through weight-sharing. We use this observation to achieve state-of-the-art HVAE performance with half the number of parameters of existing models, exploiting the properties of our continuous-time formulation.

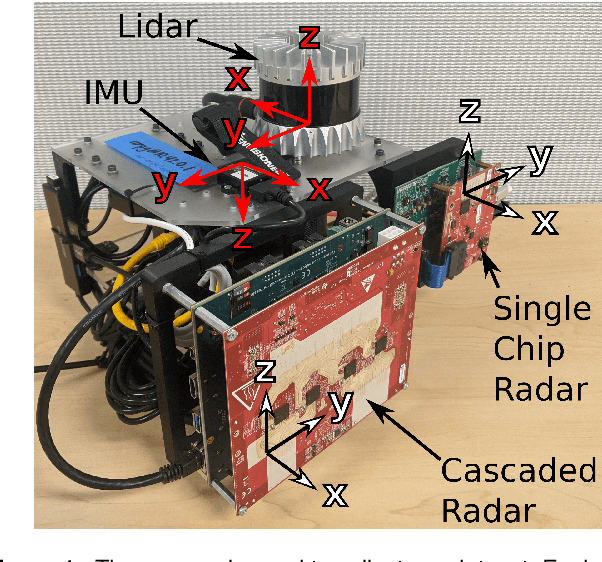
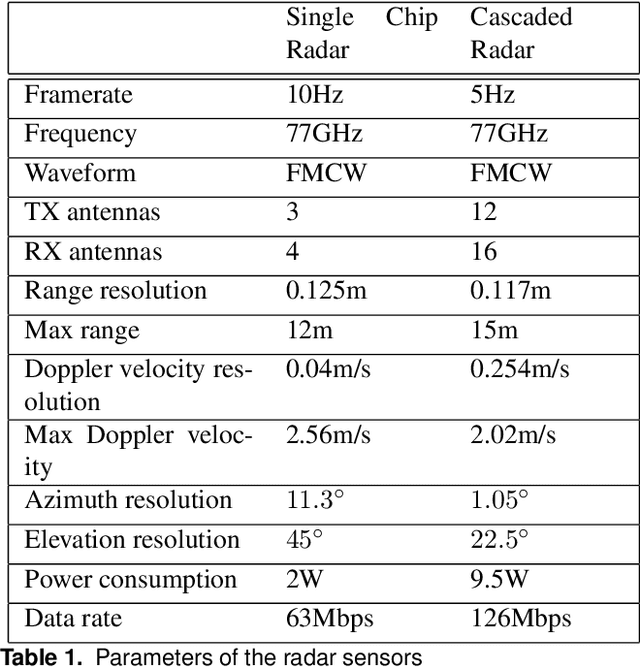
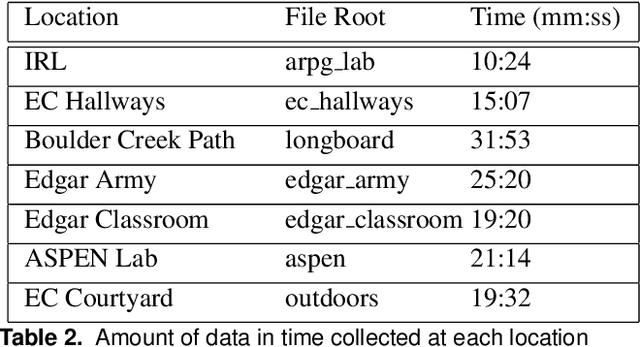
ColoRadar: The Direct 3D Millimeter Wave Radar Dataset

Millimeter wave radar is becoming increasingly popular as a sensing modality for robotic mapping and state estimation. However, there are very few publicly available datasets that include dense, high-resolution millimeter wave radar scans and there are none focused on 3D odometry and mapping. In this paper we present a solution to that problem. The ColoRadar dataset includes 3 different forms of dense, high-resolution radar data from 2 FMCW radar sensors as well as 3D lidar, IMU, and highly accurate groundtruth for the sensor rig's pose over approximately 2 hours of data collection in highly diverse 3D environments.