FunBO: Discovering Acquisition Functions for Bayesian Optimization with FunSearch

The sample efficiency of Bayesian optimization algorithms depends on carefully crafted acquisition functions (AFs) guiding the sequential collection of function evaluations. The best-performing AF can vary significantly across optimization problems, often requiring ad-hoc and problem-specific choices. This work tackles the challenge of designing novel AFs that perform well across a variety of experimental settings. Based on FunSearch, a recent work using Large Language Models (LLMs) for discovery in mathematical sciences, we propose FunBO, an LLM-based method that can be used to learn new AFs written in computer code by leveraging access to a limited number of evaluations for a set of objective functions. We provide the analytic expression of all discovered AFs and evaluate them on various global optimization benchmarks and hyperparameter optimization tasks. We show how FunBO identifies AFs that generalize well in and out of the training distribution of functions, thus outperforming established general-purpose AFs and achieving competitive performance against AFs that are customized to specific function types and are learned via transfer-learning algorithms.

Quantum Circuit Optimization with AlphaTensor

A key challenge in realizing fault-tolerant quantum computers is circuit optimization. Focusing on the most expensive gates in fault-tolerant quantum computation (namely, the T gates), we address the problem of T-count optimization, i.e., minimizing the number of T gates that are needed to implement a given circuit. To achieve this, we develop AlphaTensor-Quantum, a method based on deep reinforcement learning that exploits the relationship between optimizing T-count and tensor decomposition. Unlike existing methods for T-count optimization, AlphaTensor-Quantum can incorporate domain-specific knowledge about quantum computation and leverage gadgets, which significantly reduces the T-count of the optimized circuits. AlphaTensor-Quantum outperforms the existing methods for T-count optimization on a set of arithmetic benchmarks (even when compared without making use of gadgets). Remarkably, it discovers an efficient algorithm akin to Karatsuba's method for multiplication in finite fields. AlphaTensor-Quantum also finds the best human-designed solutions for relevant arithmetic computations used in Shor's algorithm and for quantum chemistry simulation, thus demonstrating it can save hundreds of hours of research by optimizing relevant quantum circuits in a fully automated way.

Order Matters: Probabilistic Modeling of Node Sequence for Graph Generation

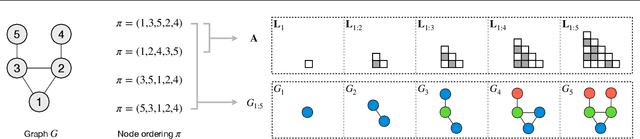
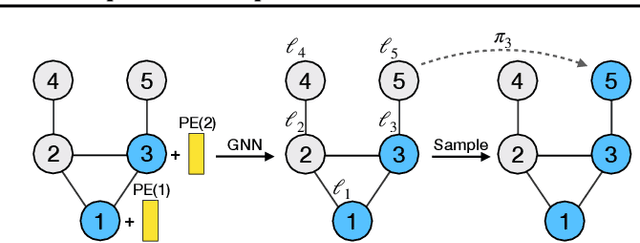
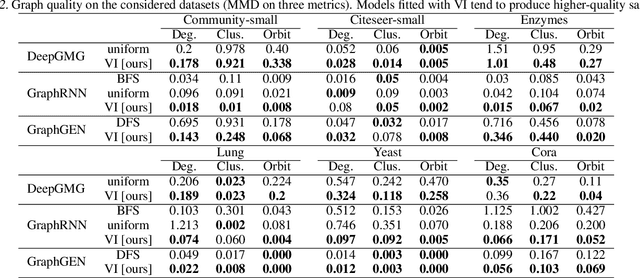
A graph generative model defines a distribution over graphs. One type of generative model is constructed by autoregressive neural networks, which sequentially add nodes and edges to generate a graph. However, the likelihood of a graph under the autoregressive model is intractable, as there are numerous sequences leading to the given graph; this makes maximum likelihood estimation challenging. Instead, in this work we derive the exact joint probability over the graph and the node ordering of the sequential process. From the joint, we approximately marginalize out the node orderings and compute a lower bound on the log-likelihood using variational inference. We train graph generative models by maximizing this bound, without using the ad-hoc node orderings of previous methods. Our experiments show that the log-likelihood bound is significantly tighter than the bound of previous schemes. Moreover, the models fitted with the proposed algorithm can generate high-quality graphs that match the structures of target graphs not seen during training. We have made our code publicly available at \hyperref[https://github.com/tufts-ml/graph-generation-vi]{https://github.com/tufts-ml/graph-generation-vi}.

VarGrad: A Low-Variance Gradient Estimator for Variational Inference

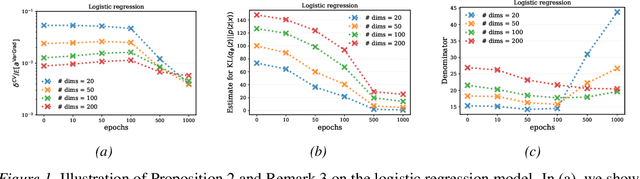
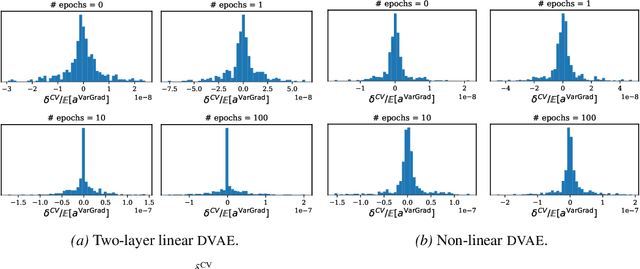
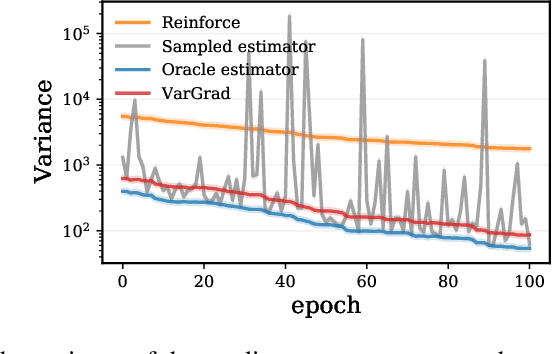
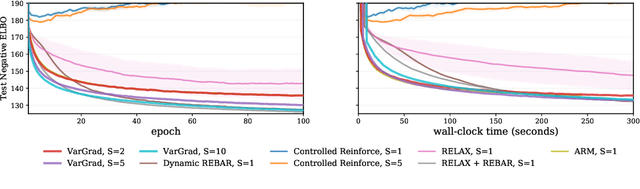
We analyse the properties of an unbiased gradient estimator of the ELBO for variational inference, based on the score function method with leave-one-out control variates. We show that this gradient estimator can be obtained using a new loss, defined as the variance of the log-ratio between the exact posterior and the variational approximation, which we call the $\textit{log-variance loss}$. Under certain conditions, the gradient of the log-variance loss equals the gradient of the (negative) ELBO. We show theoretically that this gradient estimator, which we call $\textit{VarGrad}$ due to its connection to the log-variance loss, exhibits lower variance than the score function method in certain settings, and that the leave-one-out control variate coefficients are close to the optimal ones. We empirically demonstrate that VarGrad offers a favourable variance versus computation trade-off compared to other state-of-the-art estimators on a discrete VAE.

Unbiased Gradient Estimation for Variational Auto-Encoders using Coupled Markov Chains

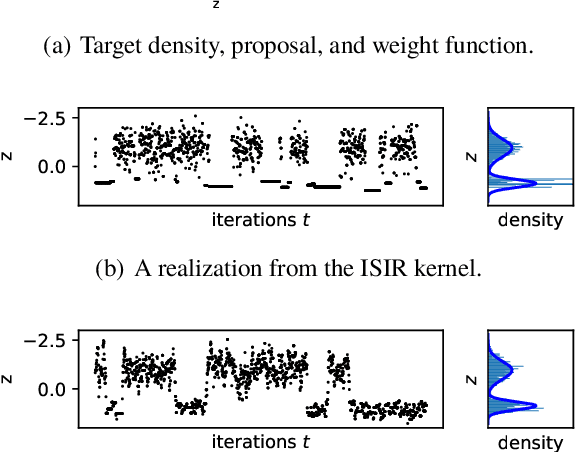
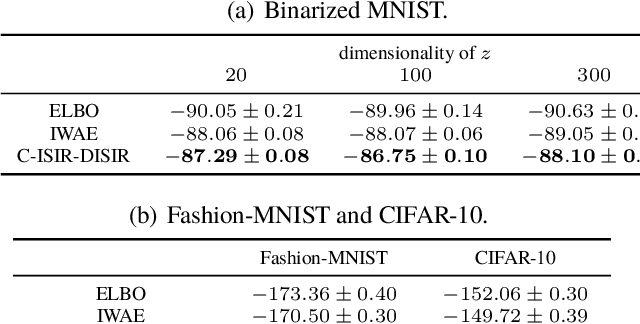
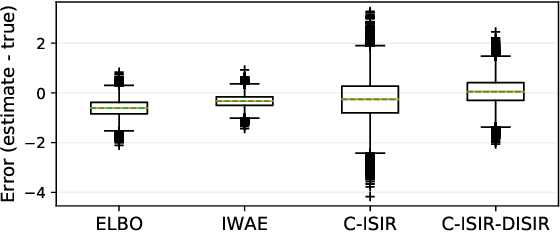
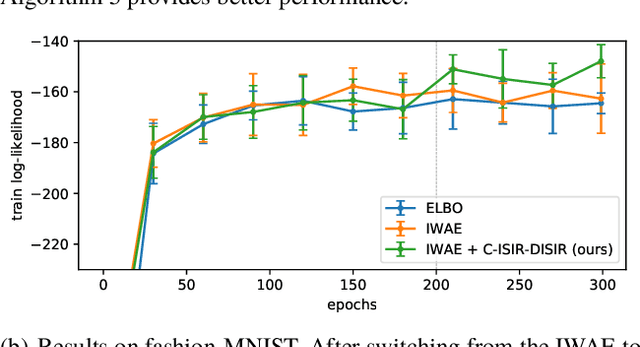
The variational auto-encoder (VAE) is a deep latent variable model that has two neural networks in an autoencoder-like architecture; one of them parameterizes the model's likelihood. Fitting its parameters via maximum likelihood is challenging since the computation of the likelihood involves an intractable integral over the latent space; thus the VAE is trained instead by maximizing a variational lower bound. Here, we develop a maximum likelihood training scheme for VAEs by introducing unbiased gradient estimators of the log-likelihood. We obtain the unbiased estimators by augmenting the latent space with a set of importance samples, similarly to the importance weighted auto-encoder (IWAE), and then constructing a Markov chain Monte Carlo (MCMC) coupling procedure on this augmented space. We provide the conditions under which the estimators can be computed in finite time and have finite variance. We demonstrate experimentally that VAEs fitted with unbiased estimators exhibit better predictive performance on three image datasets.

Prescribed Generative Adversarial Networks

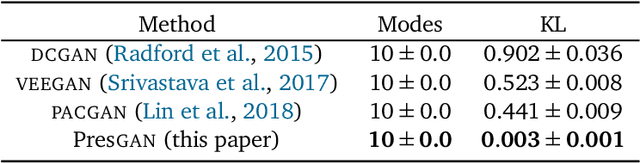
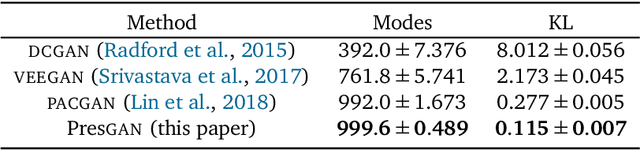
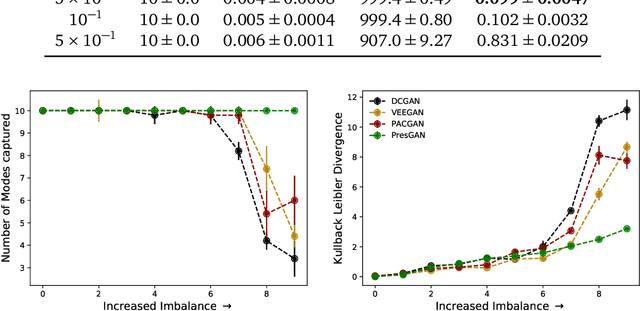
Generative adversarial networks (GANs) are a powerful approach to unsupervised learning. They have achieved state-of-the-art performance in the image domain. However, GANs are limited in two ways. They often learn distributions with low support---a phenomenon known as mode collapse---and they do not guarantee the existence of a probability density, which makes evaluating generalization using predictive log-likelihood impossible. In this paper, we develop the prescribed GAN (PresGAN) to address these shortcomings. PresGANs add noise to the output of a density network and optimize an entropy-regularized adversarial loss. The added noise renders tractable approximations of the predictive log-likelihood and stabilizes the training procedure. The entropy regularizer encourages PresGANs to capture all the modes of the data distribution. Fitting PresGANs involves computing the intractable gradients of the entropy regularization term; PresGANs sidestep this intractability using unbiased stochastic estimates. We evaluate PresGANs on several datasets and found they mitigate mode collapse and generate samples with high perceptual quality. We further found that PresGANs reduce the gap in performance in terms of predictive log-likelihood between traditional GANs and variational autoencoders (VAEs).

The Dynamic Embedded Topic Model

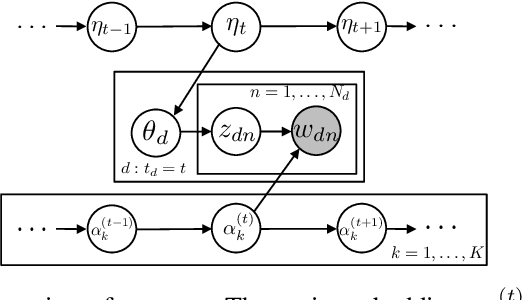
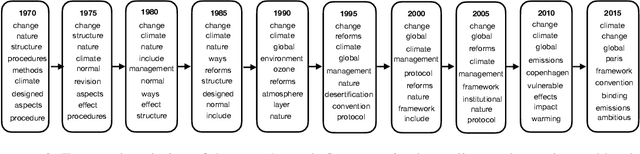
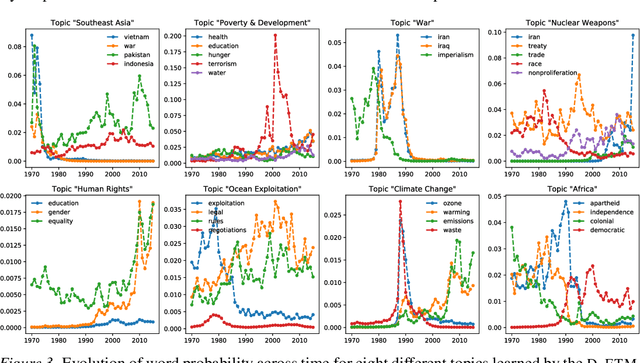
Topic modeling analyzes documents to learn meaningful patterns of words. Dynamic topic models capture how these patterns vary over time for a set of documents that were collected over a large time span. We develop the dynamic embedded topic model (D-ETM), a generative model of documents that combines dynamic latent Dirichlet allocation (D-LDA) and word embeddings. The D-ETM models each word with a categorical distribution whose parameter is given by the inner product between the word embedding and an embedding representation of its assigned topic at a particular time step. The word embeddings allow the D-ETM to generalize to rare words. The D-ETM learns smooth topic trajectories by defining a random walk prior over the embeddings of the topics. We fit the D-ETM using structured amortized variational inference. On a collection of United Nations debates, we find that the D-ETM learns interpretable topics and outperforms D-LDA in terms of both topic quality and predictive performance.

Topic Modeling in Embedding Spaces

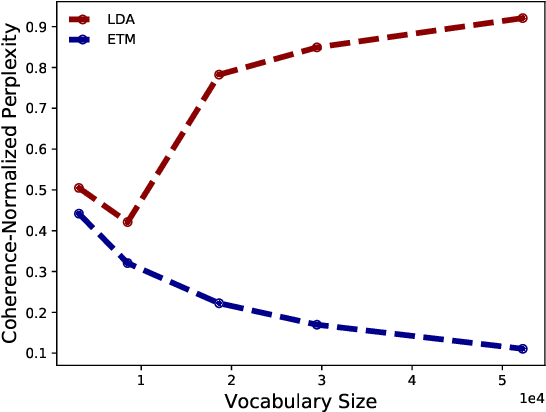
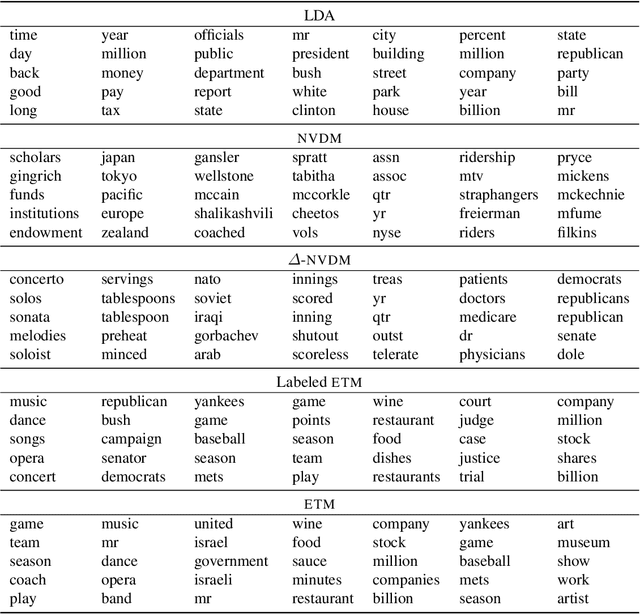
Topic modeling analyzes documents to learn meaningful patterns of words. However, existing topic models fail to learn interpretable topics when working with large and heavy-tailed vocabularies. To this end, we develop the Embedded Topic Model (ETM), a generative model of documents that marries traditional topic models with word embeddings. In particular, it models each word with a categorical distribution whose natural parameter is the inner product between a word embedding and an embedding of its assigned topic. To fit the ETM, we develop an efficient amortized variational inference algorithm. The ETM discovers interpretable topics even with large vocabularies that include rare words and stop words. It outperforms existing document models, such as latent Dirichlet allocation (LDA), in terms of both topic quality and predictive performance.

A Contrastive Divergence for Combining Variational Inference and MCMC

We develop a method to combine Markov chain Monte Carlo (MCMC) and variational inference (VI), leveraging the advantages of both inference approaches. Specifically, we improve the variational distribution by running a few MCMC steps. To make inference tractable, we introduce the variational contrastive divergence (VCD), a new divergence that replaces the standard Kullback-Leibler (KL) divergence used in VI. The VCD captures a notion of discrepancy between the initial variational distribution and its improved version (obtained after running the MCMC steps), and it converges asymptotically to the symmetrized KL divergence between the variational distribution and the posterior of interest. The VCD objective can be optimized efficiently with respect to the variational parameters via stochastic optimization. We show experimentally that optimizing the VCD leads to better predictive performance on two latent variable models: logistic matrix factorization and variational autoencoders (VAEs).

Poisson Multi-Bernoulli Mapping Using Gibbs Sampling

This paper addresses the mapping problem. Using a conjugate prior form, we derive the exact theoretical batch multi-object posterior density of the map given a set of measurements. The landmarks in the map are modeled as extended objects, and the measurements are described as a Poisson process, conditioned on the map. We use a Poisson process prior on the map and prove that the posterior distribution is a hybrid Poisson, multi-Bernoulli mixture distribution. We devise a Gibbs sampling algorithm to sample from the batch multi-object posterior. The proposed method can handle uncertainties in the data associations and the cardinality of the set of landmarks, and is parallelizable, making it suitable for large-scale problems. The performance of the proposed method is evaluated on synthetic data and is shown to outperform a state-of-the-art method.