Consistency Regularization for Variational Auto-Encoders

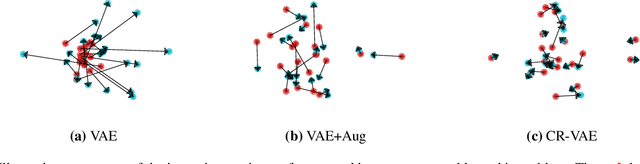
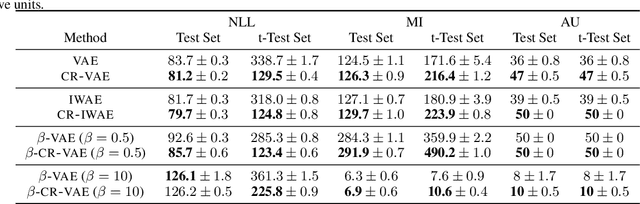
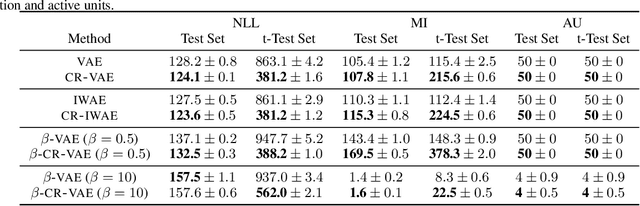
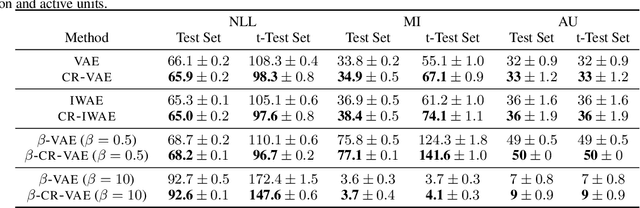
Variational auto-encoders (VAEs) are a powerful approach to unsupervised learning. They enable scalable approximate posterior inference in latent-variable models using variational inference (VI). A VAE posits a variational family parameterized by a deep neural network called an encoder that takes data as input. This encoder is shared across all the observations, which amortizes the cost of inference. However the encoder of a VAE has the undesirable property that it maps a given observation and a semantics-preserving transformation of it to different latent representations. This "inconsistency" of the encoder lowers the quality of the learned representations, especially for downstream tasks, and also negatively affects generalization. In this paper, we propose a regularization method to enforce consistency in VAEs. The idea is to minimize the Kullback-Leibler (KL) divergence between the variational distribution when conditioning on the observation and the variational distribution when conditioning on a random semantic-preserving transformation of this observation. This regularization is applicable to any VAE. In our experiments we apply it to four different VAE variants on several benchmark datasets and found it always improves the quality of the learned representations but also leads to better generalization. In particular, when applied to the Nouveau Variational Auto-Encoder (NVAE), our regularization method yields state-of-the-art performance on MNIST and CIFAR-10. We also applied our method to 3D data and found it learns representations of superior quality as measured by accuracy on a downstream classification task.

Deep Probabilistic Graphical Modeling

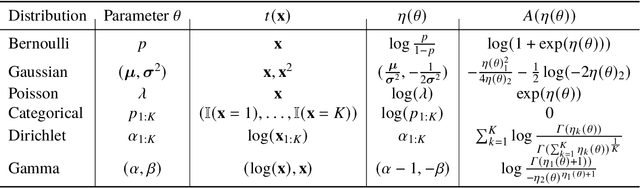
Probabilistic graphical modeling (PGM) provides a framework for formulating an interpretable generative process of data and expressing uncertainty about unknowns, but it lacks flexibility. Deep learning (DL) is an alternative framework for learning from data that has achieved great empirical success in recent years. DL offers great flexibility, but it lacks the interpretability and calibration of PGM. This thesis develops deep probabilistic graphical modeling (DPGM.) DPGM consists in leveraging DL to make PGM more flexible. DPGM brings about new methods for learning from data that exhibit the advantages of both PGM and DL. We use DL within PGM to build flexible models endowed with an interpretable latent structure. One model class we develop extends exponential family PCA using neural networks to improve predictive performance while enforcing the interpretability of the latent factors. Another model class we introduce enables accounting for long-term dependencies when modeling sequential data, which is a challenge when using purely DL or PGM approaches. Finally, DPGM successfully solves several outstanding problems of probabilistic topic models, a widely used family of models in PGM. DPGM also brings about new algorithms for learning with complex data. We develop reweighted expectation maximization, an algorithm that unifies several existing maximum likelihood-based algorithms for learning models parameterized by neural networks. This unifying view is made possible using expectation maximization, a canonical inference algorithm in PGM. We also develop entropy-regularized adversarial learning, a learning paradigm that deviates from the traditional maximum likelihood approach used in PGM. From the DL perspective, entropy-regularized adversarial learning provides a solution to the long-standing mode collapse problem of generative adversarial networks, a widely used DL approach.

Prescribed Generative Adversarial Networks

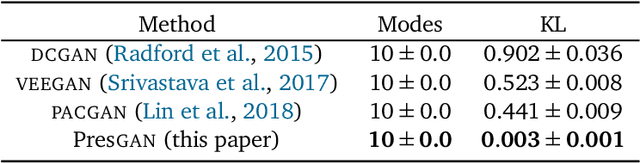
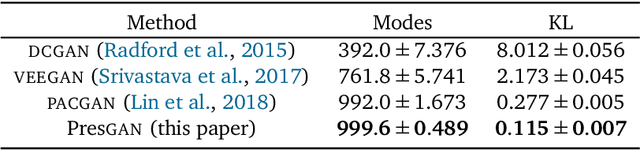
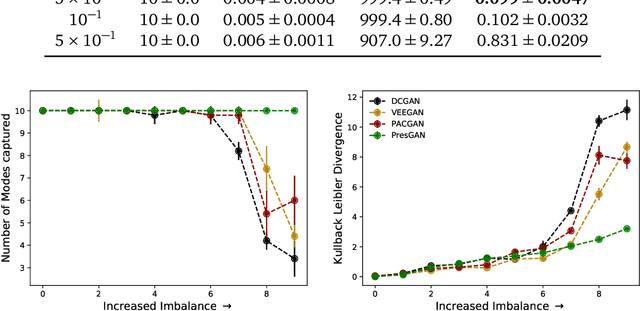
Generative adversarial networks (GANs) are a powerful approach to unsupervised learning. They have achieved state-of-the-art performance in the image domain. However, GANs are limited in two ways. They often learn distributions with low support---a phenomenon known as mode collapse---and they do not guarantee the existence of a probability density, which makes evaluating generalization using predictive log-likelihood impossible. In this paper, we develop the prescribed GAN (PresGAN) to address these shortcomings. PresGANs add noise to the output of a density network and optimize an entropy-regularized adversarial loss. The added noise renders tractable approximations of the predictive log-likelihood and stabilizes the training procedure. The entropy regularizer encourages PresGANs to capture all the modes of the data distribution. Fitting PresGANs involves computing the intractable gradients of the entropy regularization term; PresGANs sidestep this intractability using unbiased stochastic estimates. We evaluate PresGANs on several datasets and found they mitigate mode collapse and generate samples with high perceptual quality. We further found that PresGANs reduce the gap in performance in terms of predictive log-likelihood between traditional GANs and variational autoencoders (VAEs).

The Dynamic Embedded Topic Model

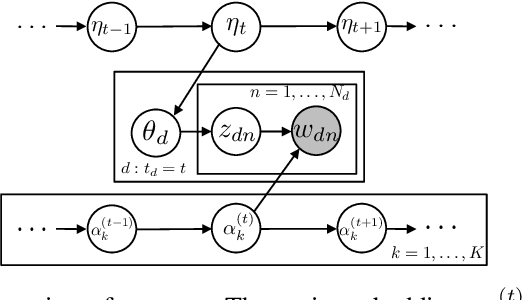
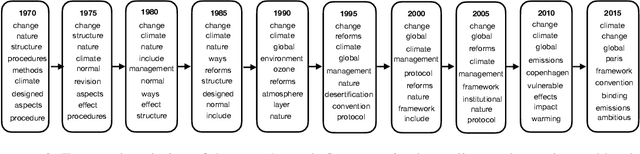
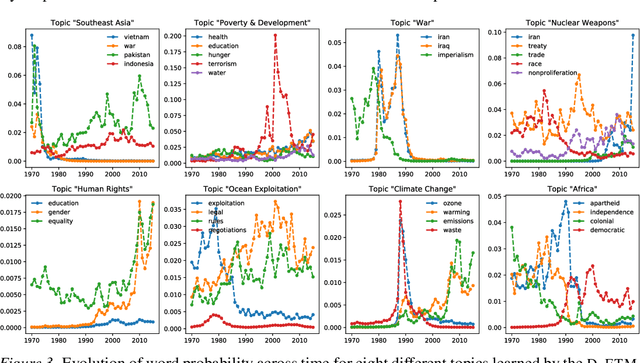
Topic modeling analyzes documents to learn meaningful patterns of words. Dynamic topic models capture how these patterns vary over time for a set of documents that were collected over a large time span. We develop the dynamic embedded topic model (D-ETM), a generative model of documents that combines dynamic latent Dirichlet allocation (D-LDA) and word embeddings. The D-ETM models each word with a categorical distribution whose parameter is given by the inner product between the word embedding and an embedding representation of its assigned topic at a particular time step. The word embeddings allow the D-ETM to generalize to rare words. The D-ETM learns smooth topic trajectories by defining a random walk prior over the embeddings of the topics. We fit the D-ETM using structured amortized variational inference. On a collection of United Nations debates, we find that the D-ETM learns interpretable topics and outperforms D-LDA in terms of both topic quality and predictive performance.

Topic Modeling in Embedding Spaces

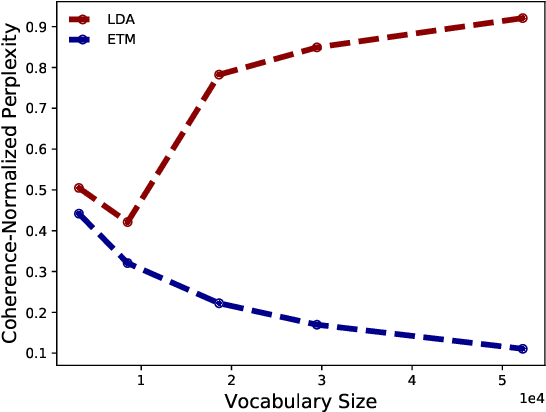
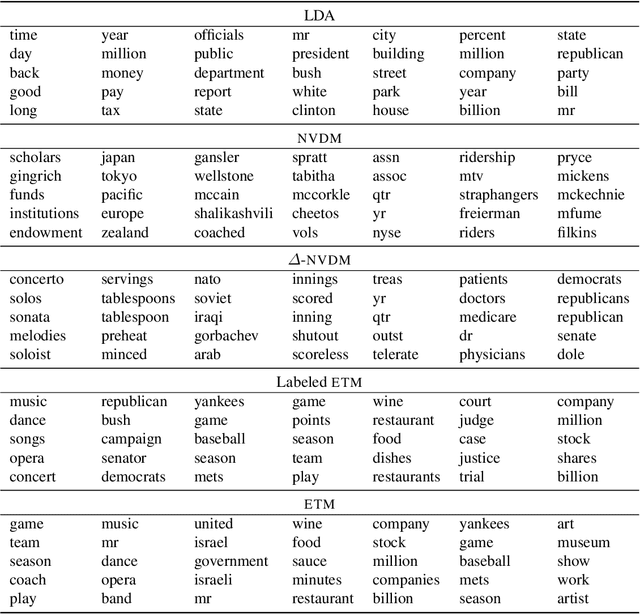
Topic modeling analyzes documents to learn meaningful patterns of words. However, existing topic models fail to learn interpretable topics when working with large and heavy-tailed vocabularies. To this end, we develop the Embedded Topic Model (ETM), a generative model of documents that marries traditional topic models with word embeddings. In particular, it models each word with a categorical distribution whose natural parameter is the inner product between a word embedding and an embedding of its assigned topic. To fit the ETM, we develop an efficient amortized variational inference algorithm. The ETM discovers interpretable topics even with large vocabularies that include rare words and stop words. It outperforms existing document models, such as latent Dirichlet allocation (LDA), in terms of both topic quality and predictive performance.

Reweighted Expectation Maximization

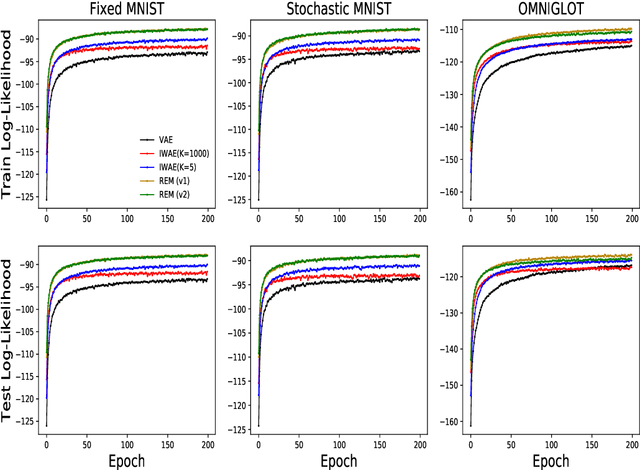
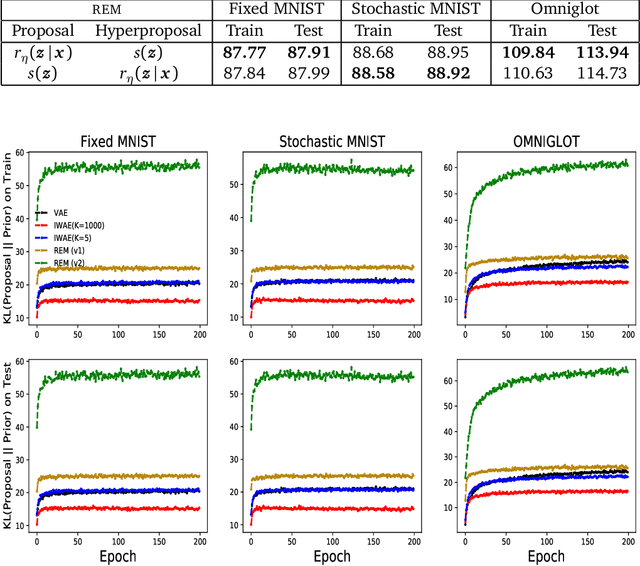
Training deep generative models with maximum likelihood remains a challenge. The typical workaround is to use variational inference (VI) and maximize a lower bound to the log marginal likelihood of the data. Variational auto-encoders (VAEs) adopt this approach. They further amortize the cost of inference by using a recognition network to parameterize the variational family. Amortized VI scales approximate posterior inference in deep generative models to large datasets. However it introduces an amortization gap and leads to approximate posteriors of reduced expressivity due to the problem known as posterior collapse. In this paper, we consider expectation maximization (EM) as a paradigm for fitting deep generative models. Unlike VI, EM directly maximizes the log marginal likelihood of the data. We rediscover the importance weighted auto-encoder (IWAE) as an instance of EM and propose a new EM-based algorithm for fitting deep generative models called reweighted expectation maximization (REM). REM learns better generative models than the IWAE by decoupling the learning dynamics of the generative model and the recognition network using a separate expressive proposal found by moment matching. We compared REM to the VAE and the IWAE on several density estimation benchmarks and found it leads to significantly better performance as measured by log-likelihood.

Noisin: Unbiased Regularization for Recurrent Neural Networks

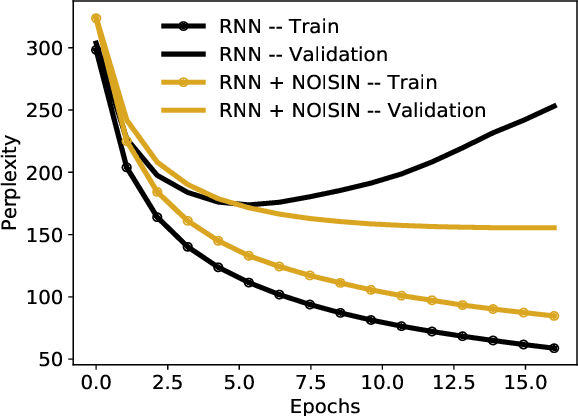
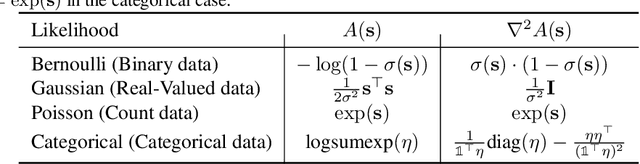
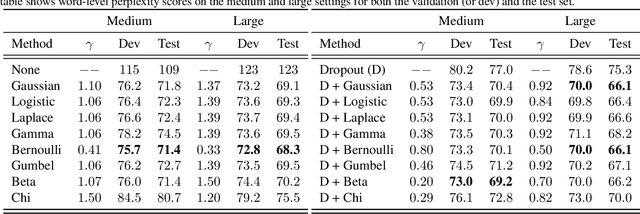
Recurrent neural networks (RNNs) are powerful models of sequential data. They have been successfully used in domains such as text and speech. However, RNNs are susceptible to overfitting; regularization is important. In this paper we develop Noisin, a new method for regularizing RNNs. Noisin injects random noise into the hidden states of the RNN and then maximizes the corresponding marginal likelihood of the data. We show how Noisin applies to any RNN and we study many different types of noise. Noisin is unbiased--it preserves the underlying RNN on average. We characterize how Noisin regularizes its RNN both theoretically and empirically. On language modeling benchmarks, Noisin improves over dropout by as much as 12.2% on the Penn Treebank and 9.4% on the Wikitext-2 dataset. We also compared the state-of-the-art language model of Yang et al. 2017, both with and without Noisin. On the Penn Treebank, the method with Noisin more quickly reaches state-of-the-art performance.

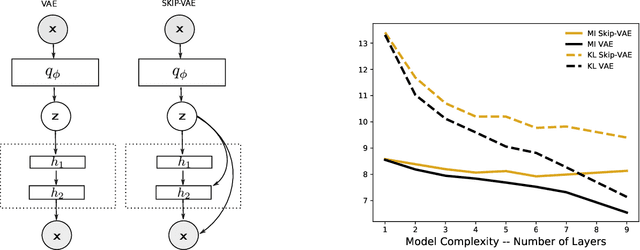
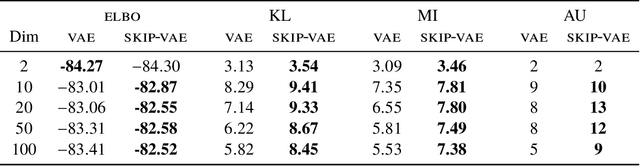
Avoiding Latent Variable Collapse With Generative Skip Models

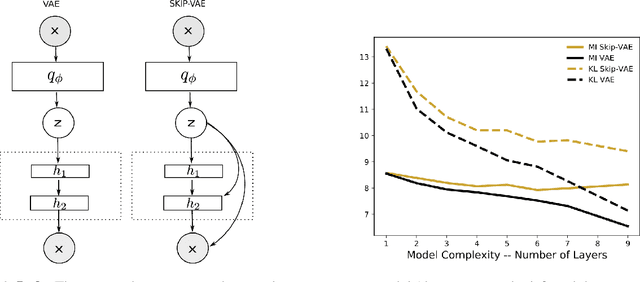
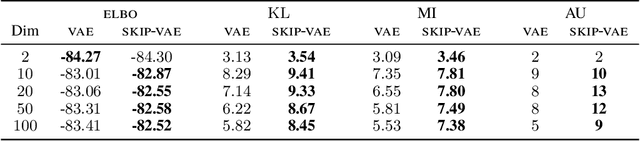
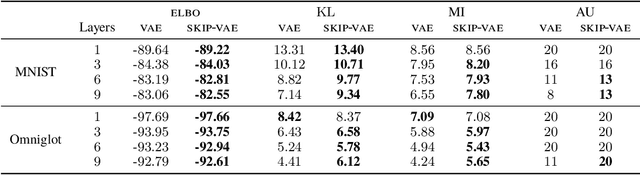
Variational autoencoders (VAEs) learn distributions of high-dimensional data. They model data by introducing a deep latent-variable model and then maximizing a lower bound of the log marginal likelihood. While VAEs can capture complex distributions, they also suffer from an issue known as "latent variable collapse." Specifically, the lower bound involves an approximate posterior of the latent variables; this posterior "collapses" when it is set equal to the prior, i.e., when the posterior is independent of the data. While VAEs learn good generative models, latent variable collapse prevents them from learning useful representations. In this paper, we propose a new way to avoid latent variable collapse. We expand the model class to one that includes skip connections; these connections enforce strong links between the latent variables and the likelihood function. We study these generative skip models both theoretically and empirically. Theoretically, we prove that skip models increase the mutual information between the observations and the inferred latent variables. Empirically, on both images (MNIST and Omniglot) and text (Yahoo), we show that generative skip models lead to less collapse than existing VAE architectures.

Augment and Reduce: Stochastic Inference for Large Categorical Distributions

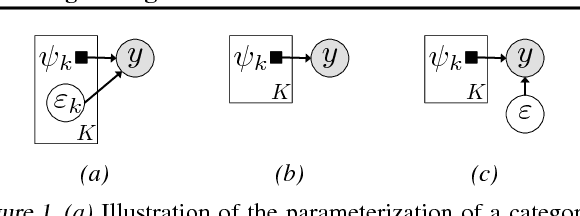
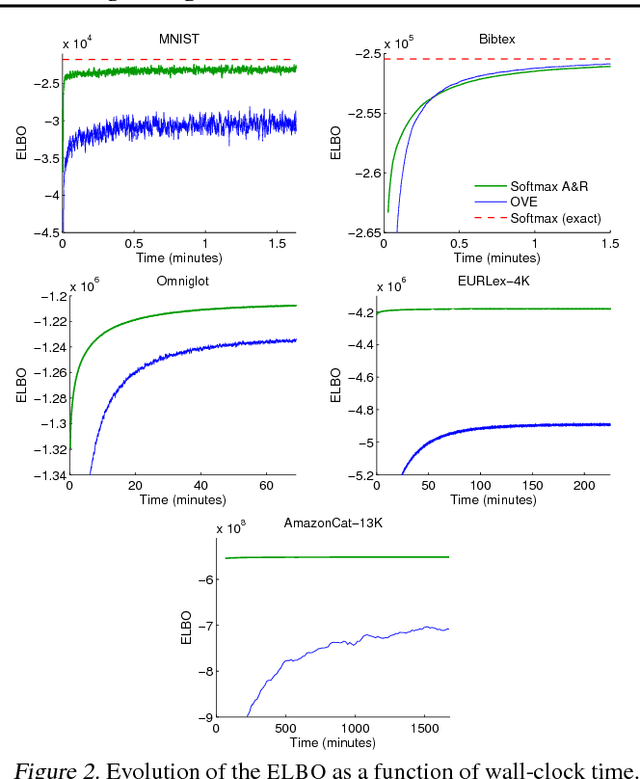
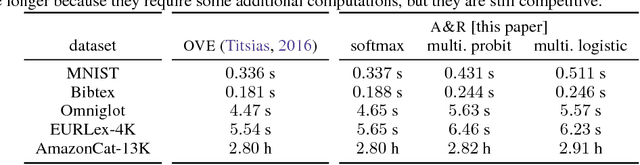
Categorical distributions are ubiquitous in machine learning, e.g., in classification, language models, and recommendation systems. However, when the number of possible outcomes is very large, using categorical distributions becomes computationally expensive, as the complexity scales linearly with the number of outcomes. To address this problem, we propose augment and reduce (A&R), a method to alleviate the computational complexity. A&R uses two ideas: latent variable augmentation and stochastic variational inference. It maximizes a lower bound on the marginal likelihood of the data. Unlike existing methods which are specific to softmax, A&R is more general and is amenable to other categorical models, such as multinomial probit. On several large-scale classification problems, we show that A&R provides a tighter bound on the marginal likelihood and has better predictive performance than existing approaches.

Variational Inference via $χ$-Upper Bound Minimization

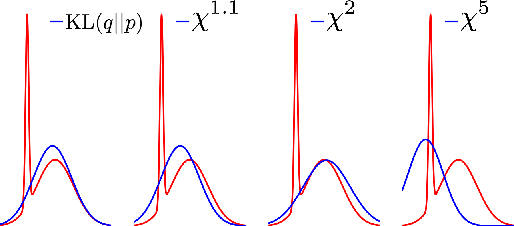
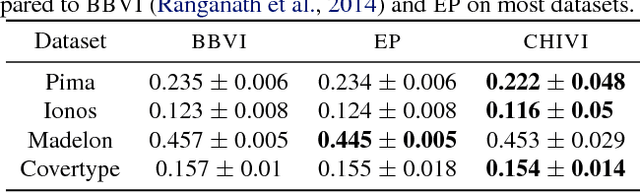
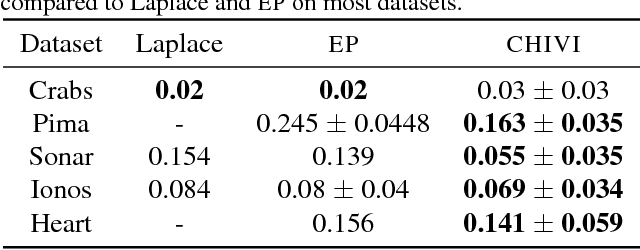
Variational inference (VI) is widely used as an efficient alternative to Markov chain Monte Carlo. It posits a family of approximating distributions $q$ and finds the closest member to the exact posterior $p$. Closeness is usually measured via a divergence $D(q || p)$ from $q$ to $p$. While successful, this approach also has problems. Notably, it typically leads to underestimation of the posterior variance. In this paper we propose CHIVI, a black-box variational inference algorithm that minimizes $D_{\chi}(p || q)$, the $\chi$-divergence from $p$ to $q$. CHIVI minimizes an upper bound of the model evidence, which we term the $\chi$ upper bound (CUBO). Minimizing the CUBO leads to improved posterior uncertainty, and it can also be used with the classical VI lower bound (ELBO) to provide a sandwich estimate of the model evidence. We study CHIVI on three models: probit regression, Gaussian process classification, and a Cox process model of basketball plays. When compared to expectation propagation and classical VI, CHIVI produces better error rates and more accurate estimates of posterior variance.