Consistency Regularization for Variational Auto-Encoders
Paper and Code
May 31, 2021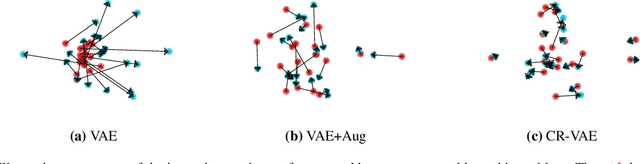
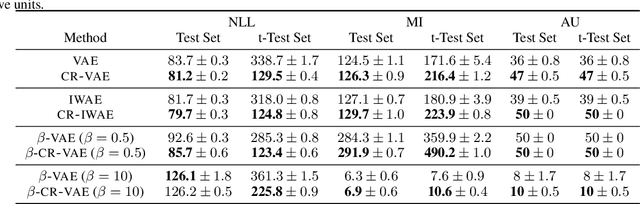
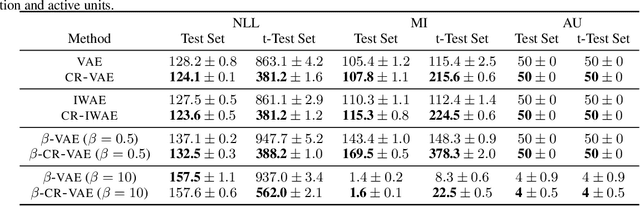
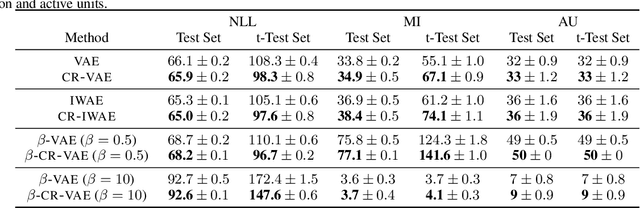
Variational auto-encoders (VAEs) are a powerful approach to unsupervised learning. They enable scalable approximate posterior inference in latent-variable models using variational inference (VI). A VAE posits a variational family parameterized by a deep neural network called an encoder that takes data as input. This encoder is shared across all the observations, which amortizes the cost of inference. However the encoder of a VAE has the undesirable property that it maps a given observation and a semantics-preserving transformation of it to different latent representations. This "inconsistency" of the encoder lowers the quality of the learned representations, especially for downstream tasks, and also negatively affects generalization. In this paper, we propose a regularization method to enforce consistency in VAEs. The idea is to minimize the Kullback-Leibler (KL) divergence between the variational distribution when conditioning on the observation and the variational distribution when conditioning on a random semantic-preserving transformation of this observation. This regularization is applicable to any VAE. In our experiments we apply it to four different VAE variants on several benchmark datasets and found it always improves the quality of the learned representations but also leads to better generalization. In particular, when applied to the Nouveau Variational Auto-Encoder (NVAE), our regularization method yields state-of-the-art performance on MNIST and CIFAR-10. We also applied our method to 3D data and found it learns representations of superior quality as measured by accuracy on a downstream classification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge