Avoiding Latent Variable Collapse With Generative Skip Models

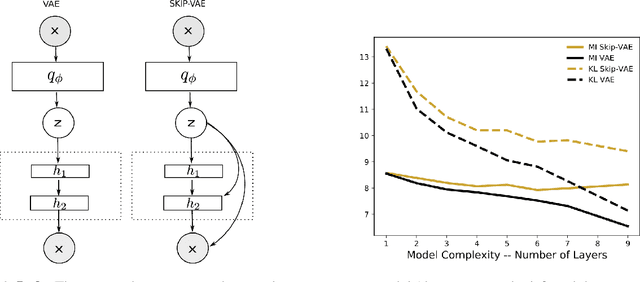
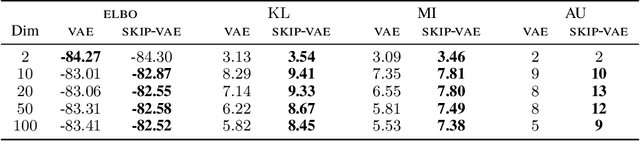
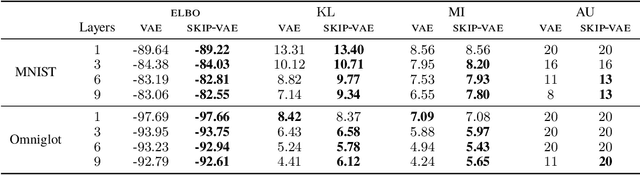
Variational autoencoders (VAEs) learn distributions of high-dimensional data. They model data by introducing a deep latent-variable model and then maximizing a lower bound of the log marginal likelihood. While VAEs can capture complex distributions, they also suffer from an issue known as "latent variable collapse." Specifically, the lower bound involves an approximate posterior of the latent variables; this posterior "collapses" when it is set equal to the prior, i.e., when the posterior is independent of the data. While VAEs learn good generative models, latent variable collapse prevents them from learning useful representations. In this paper, we propose a new way to avoid latent variable collapse. We expand the model class to one that includes skip connections; these connections enforce strong links between the latent variables and the likelihood function. We study these generative skip models both theoretically and empirically. Theoretically, we prove that skip models increase the mutual information between the observations and the inferred latent variables. Empirically, on both images (MNIST and Omniglot) and text (Yahoo), we show that generative skip models lead to less collapse than existing VAE architectures.