Deep Probabilistic Graphical Modeling

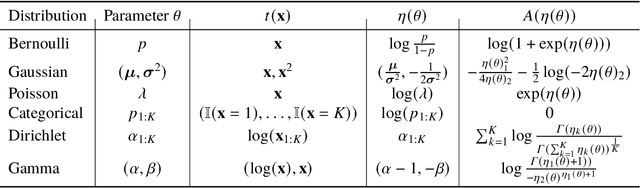
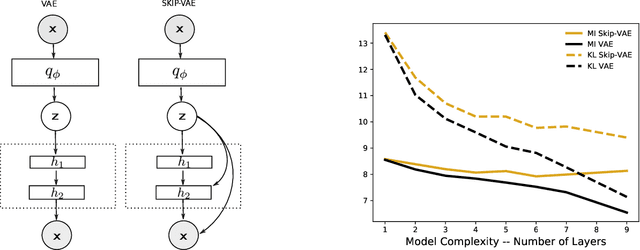
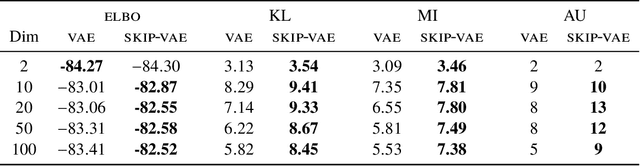
Probabilistic graphical modeling (PGM) provides a framework for formulating an interpretable generative process of data and expressing uncertainty about unknowns, but it lacks flexibility. Deep learning (DL) is an alternative framework for learning from data that has achieved great empirical success in recent years. DL offers great flexibility, but it lacks the interpretability and calibration of PGM. This thesis develops deep probabilistic graphical modeling (DPGM.) DPGM consists in leveraging DL to make PGM more flexible. DPGM brings about new methods for learning from data that exhibit the advantages of both PGM and DL. We use DL within PGM to build flexible models endowed with an interpretable latent structure. One model class we develop extends exponential family PCA using neural networks to improve predictive performance while enforcing the interpretability of the latent factors. Another model class we introduce enables accounting for long-term dependencies when modeling sequential data, which is a challenge when using purely DL or PGM approaches. Finally, DPGM successfully solves several outstanding problems of probabilistic topic models, a widely used family of models in PGM. DPGM also brings about new algorithms for learning with complex data. We develop reweighted expectation maximization, an algorithm that unifies several existing maximum likelihood-based algorithms for learning models parameterized by neural networks. This unifying view is made possible using expectation maximization, a canonical inference algorithm in PGM. We also develop entropy-regularized adversarial learning, a learning paradigm that deviates from the traditional maximum likelihood approach used in PGM. From the DL perspective, entropy-regularized adversarial learning provides a solution to the long-standing mode collapse problem of generative adversarial networks, a widely used DL approach.