Reweighted Expectation Maximization
Paper and Code
Jun 13, 2019
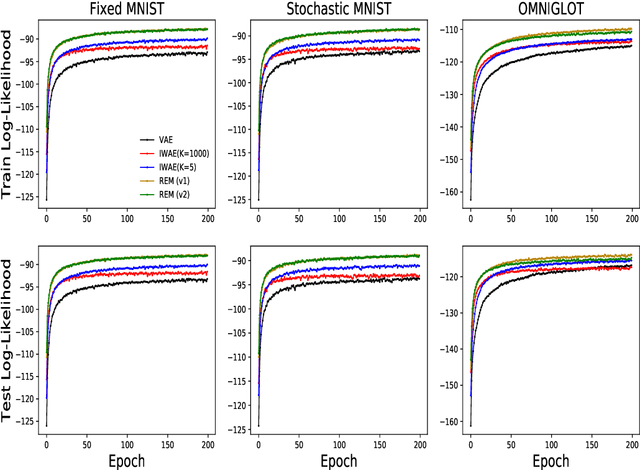
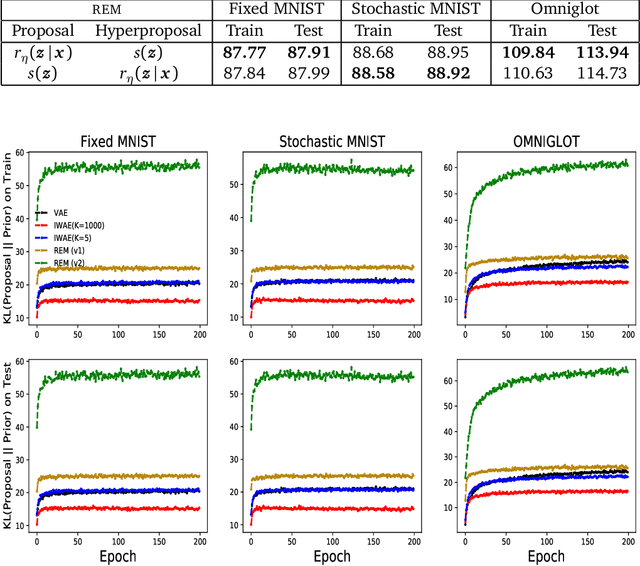
Training deep generative models with maximum likelihood remains a challenge. The typical workaround is to use variational inference (VI) and maximize a lower bound to the log marginal likelihood of the data. Variational auto-encoders (VAEs) adopt this approach. They further amortize the cost of inference by using a recognition network to parameterize the variational family. Amortized VI scales approximate posterior inference in deep generative models to large datasets. However it introduces an amortization gap and leads to approximate posteriors of reduced expressivity due to the problem known as posterior collapse. In this paper, we consider expectation maximization (EM) as a paradigm for fitting deep generative models. Unlike VI, EM directly maximizes the log marginal likelihood of the data. We rediscover the importance weighted auto-encoder (IWAE) as an instance of EM and propose a new EM-based algorithm for fitting deep generative models called reweighted expectation maximization (REM). REM learns better generative models than the IWAE by decoupling the learning dynamics of the generative model and the recognition network using a separate expressive proposal found by moment matching. We compared REM to the VAE and the IWAE on several density estimation benchmarks and found it leads to significantly better performance as measured by log-likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge