Unbiased Gradient Estimation for Variational Auto-Encoders using Coupled Markov Chains
Paper and Code
Oct 05, 2020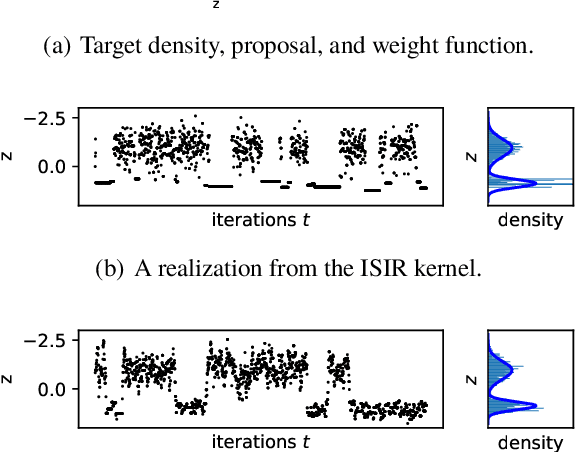
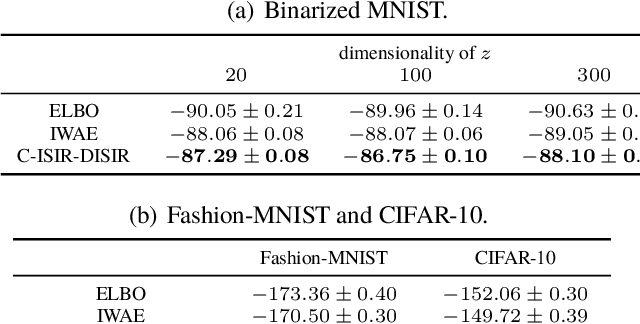
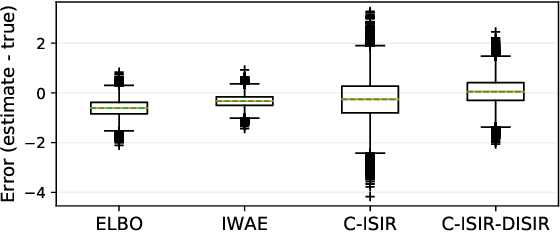
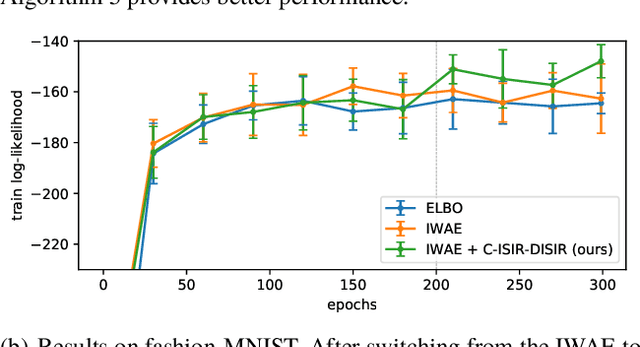
The variational auto-encoder (VAE) is a deep latent variable model that has two neural networks in an autoencoder-like architecture; one of them parameterizes the model's likelihood. Fitting its parameters via maximum likelihood is challenging since the computation of the likelihood involves an intractable integral over the latent space; thus the VAE is trained instead by maximizing a variational lower bound. Here, we develop a maximum likelihood training scheme for VAEs by introducing unbiased gradient estimators of the log-likelihood. We obtain the unbiased estimators by augmenting the latent space with a set of importance samples, similarly to the importance weighted auto-encoder (IWAE), and then constructing a Markov chain Monte Carlo (MCMC) coupling procedure on this augmented space. We provide the conditions under which the estimators can be computed in finite time and have finite variance. We demonstrate experimentally that VAEs fitted with unbiased estimators exhibit better predictive performance on three image datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge