Quantum Circuit Optimization with AlphaTensor

A key challenge in realizing fault-tolerant quantum computers is circuit optimization. Focusing on the most expensive gates in fault-tolerant quantum computation (namely, the T gates), we address the problem of T-count optimization, i.e., minimizing the number of T gates that are needed to implement a given circuit. To achieve this, we develop AlphaTensor-Quantum, a method based on deep reinforcement learning that exploits the relationship between optimizing T-count and tensor decomposition. Unlike existing methods for T-count optimization, AlphaTensor-Quantum can incorporate domain-specific knowledge about quantum computation and leverage gadgets, which significantly reduces the T-count of the optimized circuits. AlphaTensor-Quantum outperforms the existing methods for T-count optimization on a set of arithmetic benchmarks (even when compared without making use of gadgets). Remarkably, it discovers an efficient algorithm akin to Karatsuba's method for multiplication in finite fields. AlphaTensor-Quantum also finds the best human-designed solutions for relevant arithmetic computations used in Shor's algorithm and for quantum chemistry simulation, thus demonstrating it can save hundreds of hours of research by optimizing relevant quantum circuits in a fully automated way.

Learning to Decode the Surface Code with a Recurrent, Transformer-Based Neural Network

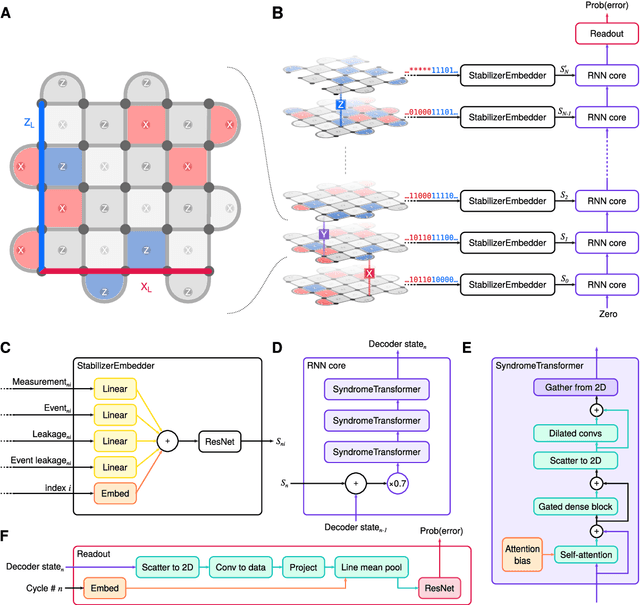
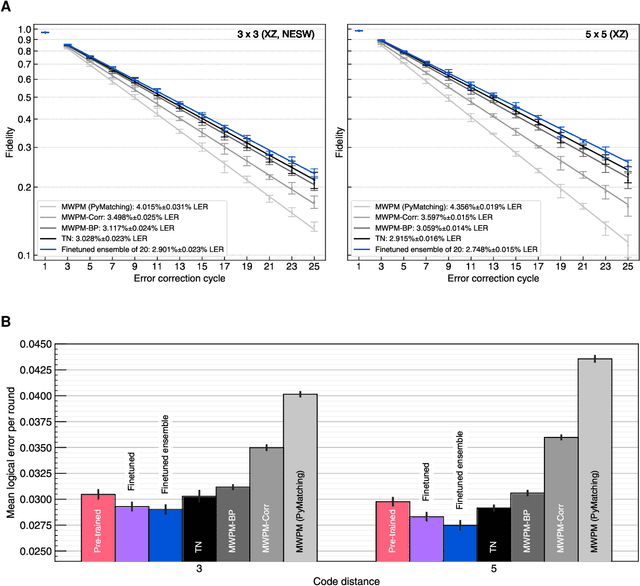
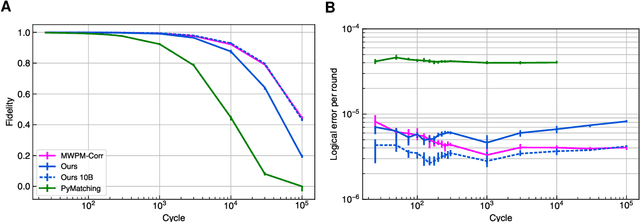
Quantum error-correction is a prerequisite for reliable quantum computation. Towards this goal, we present a recurrent, transformer-based neural network which learns to decode the surface code, the leading quantum error-correction code. Our decoder outperforms state-of-the-art algorithmic decoders on real-world data from Google's Sycamore quantum processor for distance 3 and 5 surface codes. On distances up to 11, the decoder maintains its advantage on simulated data with realistic noise including cross-talk, leakage, and analog readout signals, and sustains its accuracy far beyond the 25 cycles it was trained on. Our work illustrates the ability of machine learning to go beyond human-designed algorithms by learning from data directly, highlighting machine learning as a strong contender for decoding in quantum computers.

Recurrent Quantum Neural Networks

Recurrent neural networks are the foundation of many sequence-to-sequence models in machine learning, such as machine translation and speech synthesis. In contrast, applied quantum computing is in its infancy. Nevertheless there already exist quantum machine learning models such as variational quantum eigensolvers which have been used successfully e.g. in the context of energy minimization tasks. In this work we construct a quantum recurrent neural network (QRNN) with demonstrable performance on non-trivial tasks such as sequence learning and integer digit classification. The QRNN cell is built from parametrized quantum neurons, which, in conjunction with amplitude amplification, create a nonlinear activation of polynomials of its inputs and cell state, and allow the extraction of a probability distribution over predicted classes at each step. To study the model's performance, we provide an implementation in pytorch, which allows the relatively efficient optimization of parametrized quantum circuits with thousands of parameters. We establish a QRNN training setup by benchmarking optimization hyperparameters, and analyse suitable network topologies for simple memorisation and sequence prediction tasks from Elman's seminal paper (1990) on temporal structure learning. We then proceed to evaluate the QRNN on MNIST classification, both by feeding the QRNN each image pixel-by-pixel; and by utilising modern data augmentation as preprocessing step. Finally, we analyse to what extent the unitary nature of the network counteracts the vanishing gradient problem that plagues many existing quantum classifiers and classical RNNs.

A Quantum Search Decoder for Natural Language Processing

Probabilistic language models, e.g. those based on an LSTM, often face the problem of finding a high probability prediction from a sequence of random variables over a set of words. This is commonly addressed using a form of greedy decoding such as beam search, where a limited number of highest-likelihood paths (the beam width) of the decoder are kept, and at the end the maximum-likelihood path is chosen. The resulting algorithm has linear runtime in the beam width. However, the input is not necessarily distributed such that a high-likelihood input symbol at any given time step also leads to the global optimum. Limiting the beam width can thus result in a failure to recognise long-range dependencies. In practice, only an exponentially large beam width can guarantee that the global optimum is found: for an input of length $n$ and average parser branching ratio $R$, the baseline classical algorithm needs to query the input on average $R^n$ times. In this work, we construct a quantum algorithm to find the globally optimal parse with high constant success probability. Given the input to the decoder is distributed like a power-law with exponent $k>0$, our algorithm yields a runtime $R^{n f(R,k)}$, where $f\le 1/2$, and $f\rightarrow 0$ exponentially quickly for growing $k$. This implies that our algorithm always yields a super-Grover type speedup, i.e. it is more than quadratically faster than its classical counterpart. We further modify our procedure to recover a quantum beam search variant, which enables an even stronger empirical speedup, while sacrificing accuracy. Finally, we apply this quantum beam search decoder to Mozilla's implementation of Baidu's DeepSpeech neural net, which we show to exhibit such a power law word rank frequency, underpinning the applicability of our model.

Classifying Data with Local Hamiltonians

The goal of this work is to define a notion of a quantum neural network to classify data, which exploits the low energy spectrum of a local Hamiltonian. As a concrete application, we build a binary classifier, train it on some actual data and then test its performance on a simple classification task. More specifically, we use Microsoft's quantum simulator, Liquid, to construct local Hamiltonians that can encode trained classifier functions in their ground space, and which can be probed by measuring the overlap with test states corresponding to the data to be classified. To obtain such a classifier Hamiltonian, we further propose a training scheme based on quantum annealing which is completely closed-off to the environment and which does not depend on external measurements until the very end, avoiding unnecessary decoherence during the annealing procedure. For a network of size n, the trained network can be stored as a list of O(n) coupling strengths. We address the question of which interactions are most suitable for a given classification task, and develop a qubit-saving optimization for the training procedure on a simulated annealing device. Furthermore, a small neural network to classify colors into red vs. blue is trained and tested, and benchmarked against the annealing parameters.

Quantum Codes from Neural Networks

We report on the usefulness of using neural networks as a variational state ansatz for many-body quantum systems in the context of quantum information-processing tasks. In the neural network state ansatz, the complex amplitude function of a quantum state is computed by a neural network. The resulting multipartite entanglement structure captured by this ansatz has proven rich enough to describe the ground states and unitary dynamics of various physical systems of interest. In the present paper, we supply further evidence for the usefulness of neural network states to describe multipartite entanglement. We demonstrate that neural network states are capable of efficiently representing quantum codes for quantum information transmission and quantum error correction. In particular, we show that a) neural network states yield quantum codes with a high coherent information for two important quantum channels, the depolarizing channel and the dephrasure channel; b) neural network states can be used to represent absolutely maximally entangled states, a special type of quantum error correction codes. In both cases, the neural network state ansatz provides an efficient and versatile means as variational parametrization of these states.