Information-theoretic generalization bounds for learning from quantum data

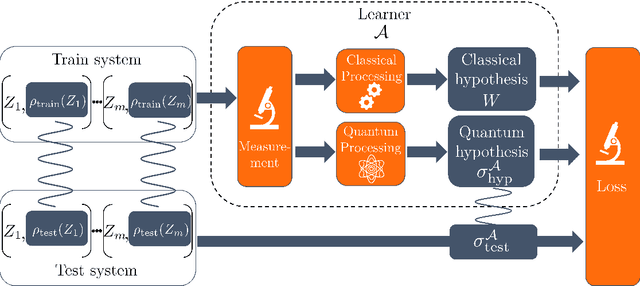
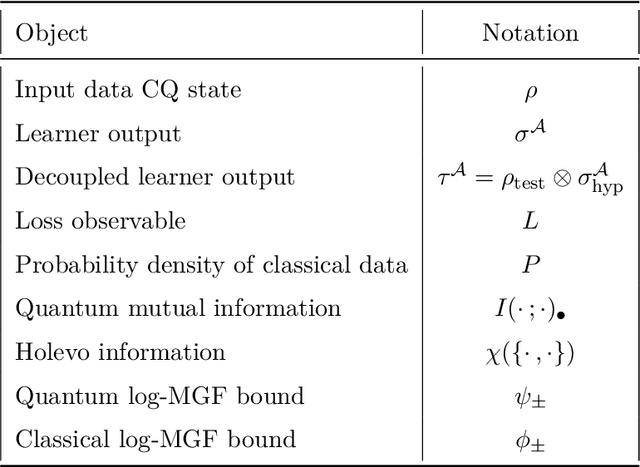
Learning tasks play an increasingly prominent role in quantum information and computation. They range from fundamental problems such as state discrimination and metrology over the framework of quantum probably approximately correct (PAC) learning, to the recently proposed shadow variants of state tomography. However, the many directions of quantum learning theory have so far evolved separately. We propose a general mathematical formalism for describing quantum learning by training on classical-quantum data and then testing how well the learned hypothesis generalizes to new data. In this framework, we prove bounds on the expected generalization error of a quantum learner in terms of classical and quantum information-theoretic quantities measuring how strongly the learner's hypothesis depends on the specific data seen during training. To achieve this, we use tools from quantum optimal transport and quantum concentration inequalities to establish non-commutative versions of decoupling lemmas that underlie recent information-theoretic generalization bounds for classical machine learning. Our framework encompasses and gives intuitively accessible generalization bounds for a variety of quantum learning scenarios such as quantum state discrimination, PAC learning quantum states, quantum parameter estimation, and quantumly PAC learning classical functions. Thereby, our work lays a foundation for a unifying quantum information-theoretic perspective on quantum learning.

Quantum Ridgelet Transform: Winning Lottery Ticket of Neural Networks with Quantum Computation

Ridgelet transform has been a fundamental mathematical tool in the theoretical studies of neural networks. However, the practical applicability of ridgelet transform to conducting learning tasks was limited since its numerical implementation by conventional classical computation requires an exponential runtime $\exp(O(D))$ as data dimension $D$ increases. To address this problem, we develop a quantum ridgelet transform (QRT), which implements the ridgelet transform of a quantum state within a linear runtime $O(D)$ of quantum computation. As an application, we also show that one can use QRT as a fundamental subroutine for quantum machine learning (QML) to efficiently find a sparse trainable subnetwork of large shallow wide neural networks without conducting large-scale optimization of the original network. This application discovers an efficient way in this regime to demonstrate the lottery ticket hypothesis on finding such a sparse trainable neural network. These results open an avenue of QML for accelerating learning tasks with commonly used classical neural networks.

Fast Quantum Algorithm for Learning with Optimized Random Features

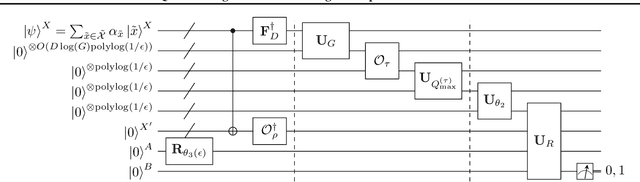
Kernel methods augmented with random features give scalable algorithms for learning from big data. But it has been computationally hard to sample random features according to a probability distribution that is optimized for the data, so as to minimize the required number of features for achieving the learning to a desired accuracy. Here, we develop a quantum algorithm for sampling from this optimized distribution over features, in runtime $O(D)$ that is linear in the dimension $D$ of the input data. Our algorithm achieves an exponential speedup in $D$ compared to any known classical algorithm for this sampling task. In contrast to existing quantum machine learning algorithms, our algorithm circumvents sparsity and low-rank assumptions and thus has wide applicability. We also show that the sampled features can be combined with regression by stochastic gradient descent to achieve the learning without canceling out our exponential speedup. Our algorithm based on sampling optimized random features leads to an accelerated framework for machine learning that takes advantage of quantum computers.

A Quantum Search Decoder for Natural Language Processing

Probabilistic language models, e.g. those based on an LSTM, often face the problem of finding a high probability prediction from a sequence of random variables over a set of words. This is commonly addressed using a form of greedy decoding such as beam search, where a limited number of highest-likelihood paths (the beam width) of the decoder are kept, and at the end the maximum-likelihood path is chosen. The resulting algorithm has linear runtime in the beam width. However, the input is not necessarily distributed such that a high-likelihood input symbol at any given time step also leads to the global optimum. Limiting the beam width can thus result in a failure to recognise long-range dependencies. In practice, only an exponentially large beam width can guarantee that the global optimum is found: for an input of length $n$ and average parser branching ratio $R$, the baseline classical algorithm needs to query the input on average $R^n$ times. In this work, we construct a quantum algorithm to find the globally optimal parse with high constant success probability. Given the input to the decoder is distributed like a power-law with exponent $k>0$, our algorithm yields a runtime $R^{n f(R,k)}$, where $f\le 1/2$, and $f\rightarrow 0$ exponentially quickly for growing $k$. This implies that our algorithm always yields a super-Grover type speedup, i.e. it is more than quadratically faster than its classical counterpart. We further modify our procedure to recover a quantum beam search variant, which enables an even stronger empirical speedup, while sacrificing accuracy. Finally, we apply this quantum beam search decoder to Mozilla's implementation of Baidu's DeepSpeech neural net, which we show to exhibit such a power law word rank frequency, underpinning the applicability of our model.