Distillation of Discrete Diffusion through Dimensional Correlations

Diffusion models have demonstrated exceptional performances in various fields of generative modeling. While they often outperform competitors including VAEs and GANs in sample quality and diversity, they suffer from slow sampling speed due to their iterative nature. Recently, distillation techniques and consistency models are mitigating this issue in continuous domains, but discrete diffusion models have some specific challenges towards faster generation. Most notably, in the current literature, correlations between different dimensions (pixels, locations) are ignored, both by its modeling and loss functions, due to computational limitations. In this paper, we propose "mixture" models in discrete diffusion that are capable of treating dimensional correlations while remaining scalable, and we provide a set of loss functions for distilling the iterations of existing models. Two primary theoretical insights underpin our approach: first, that dimensionally independent models can well approximate the data distribution if they are allowed to conduct many sampling steps, and second, that our loss functions enables mixture models to distill such many-step conventional models into just a few steps by learning the dimensional correlations. We empirically demonstrate that our proposed method for discrete diffusions work in practice, by distilling a continuous-time discrete diffusion model pretrained on the CIFAR-10 dataset.

$\textit{Jump Your Steps}$: Optimizing Sampling Schedule of Discrete Diffusion Models

Diffusion models have seen notable success in continuous domains, leading to the development of discrete diffusion models (DDMs) for discrete variables. Despite recent advances, DDMs face the challenge of slow sampling speeds. While parallel sampling methods like $\tau$-leaping accelerate this process, they introduce $\textit{Compounding Decoding Error}$ (CDE), where discrepancies arise between the true distribution and the approximation from parallel token generation, leading to degraded sample quality. In this work, we present $\textit{Jump Your Steps}$ (JYS), a novel approach that optimizes the allocation of discrete sampling timesteps by minimizing CDE without extra computational cost. More precisely, we derive a practical upper bound on CDE and propose an efficient algorithm for searching for the optimal sampling schedule. Extensive experiments across image, music, and text generation show that JYS significantly improves sampling quality, establishing it as a versatile framework for enhancing DDM performance for fast sampling.

A Quadrature Approach for General-Purpose Batch Bayesian Optimization via Probabilistic Lifting

Parallelisation in Bayesian optimisation is a common strategy but faces several challenges: the need for flexibility in acquisition functions and kernel choices, flexibility dealing with discrete and continuous variables simultaneously, model misspecification, and lastly fast massive parallelisation. To address these challenges, we introduce a versatile and modular framework for batch Bayesian optimisation via probabilistic lifting with kernel quadrature, called SOBER, which we present as a Python library based on GPyTorch/BoTorch. Our framework offers the following unique benefits: (1) Versatility in downstream tasks under a unified approach. (2) A gradient-free sampler, which does not require the gradient of acquisition functions, offering domain-agnostic sampling (e.g., discrete and mixed variables, non-Euclidean space). (3) Flexibility in domain prior distribution. (4) Adaptive batch size (autonomous determination of the optimal batch size). (5) Robustness against a misspecified reproducing kernel Hilbert space. (6) Natural stopping criterion.

Policy Gradient with Kernel Quadrature

Reward evaluation of episodes becomes a bottleneck in a broad range of reinforcement learning tasks. Our aim in this paper is to select a small but representative subset of a large batch of episodes, only on which we actually compute rewards for more efficient policy gradient iterations. We build a Gaussian process modeling of discounted returns or rewards to derive a positive definite kernel on the space of episodes, run an "episodic" kernel quadrature method to compress the information of sample episodes, and pass the reduced episodes to the policy network for gradient updates. We present the theoretical background of this procedure as well as its numerical illustrations in MuJoCo and causal discovery tasks.

Domain-Agnostic Batch Bayesian Optimization with Diverse Constraints via Bayesian Quadrature

Real-world optimisation problems often feature complex combinations of (1) diverse constraints, (2) discrete and mixed spaces, and are (3) highly parallelisable. (4) There are also cases where the objective function cannot be queried if unknown constraints are not satisfied, e.g. in drug discovery, safety on animal experiments (unknown constraints) must be established before human clinical trials (querying objective function) may proceed. However, most existing works target each of the above three problems in isolation and do not consider (4) unknown constraints with query rejection. For problems with diverse constraints and/or unconventional input spaces, it is difficult to apply these techniques as they are often mutually incompatible. We propose cSOBER, a domain-agnostic prudent parallel active sampler for Bayesian optimisation, based on SOBER of Adachi et al. (2023). We consider infeasibility under unknown constraints as a type of integration error that we can estimate. We propose a theoretically-driven approach that propagates such error as a tolerance in the quadrature precision that automatically balances exploitation and exploration with the expected rejection rate. Moreover, our method flexibly accommodates diverse constraints and/or discrete and mixed spaces via adaptive tolerance, including conventional zero-risk cases. We show that cSOBER outperforms competitive baselines on diverse real-world blackbox-constrained problems, including safety-constrained drug discovery, and human-relationship-aware team optimisation over graph-structured space.

SOBER: Scalable Batch Bayesian Optimization and Quadrature using Recombination Constraints

Batch Bayesian optimisation (BO) has shown to be a sample-efficient method of performing optimisation where expensive-to-evaluate objective functions can be queried in parallel. However, current methods do not scale to large batch sizes -- a frequent desideratum in practice (e.g. drug discovery or simulation-based inference). We present a novel algorithm, SOBER, which permits scalable and diversified batch BO with arbitrary acquisition functions, arbitrary input spaces (e.g. graph), and arbitrary kernels. The key to our approach is to reformulate batch selection for BO as a Bayesian quadrature (BQ) problem, which offers computational advantages. This reformulation is beneficial in solving BQ tasks reciprocally, which introduces the exploitative functionality of BO to BQ. We show that SOBER offers substantive performance gains in synthetic and real-world tasks, including drug discovery and simulation-based inference.

Quantum Ridgelet Transform: Winning Lottery Ticket of Neural Networks with Quantum Computation

Ridgelet transform has been a fundamental mathematical tool in the theoretical studies of neural networks. However, the practical applicability of ridgelet transform to conducting learning tasks was limited since its numerical implementation by conventional classical computation requires an exponential runtime $\exp(O(D))$ as data dimension $D$ increases. To address this problem, we develop a quantum ridgelet transform (QRT), which implements the ridgelet transform of a quantum state within a linear runtime $O(D)$ of quantum computation. As an application, we also show that one can use QRT as a fundamental subroutine for quantum machine learning (QML) to efficiently find a sparse trainable subnetwork of large shallow wide neural networks without conducting large-scale optimization of the original network. This application discovers an efficient way in this regime to demonstrate the lottery ticket hypothesis on finding such a sparse trainable neural network. These results open an avenue of QML for accelerating learning tasks with commonly used classical neural networks.

Sampling-based Nyström Approximation and Kernel Quadrature

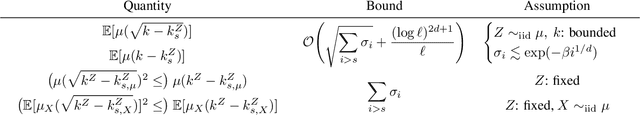
We analyze the Nystr\"om approximation of a positive definite kernel associated with a probability measure. We first prove an improved error bound for the conventional Nystr\"om approximation with i.i.d. sampling and singular-value decomposition in the continuous regime; the proof techniques are borrowed from statistical learning theory. We further introduce a refined selection of subspaces in Nystr\"om approximation with theoretical guarantees that is applicable to non-i.i.d. landmark points. Finally, we discuss their application to convex kernel quadrature and give novel theoretical guarantees as well as numerical observations.

Fast Bayesian Inference with Batch Bayesian Quadrature via Kernel Recombination

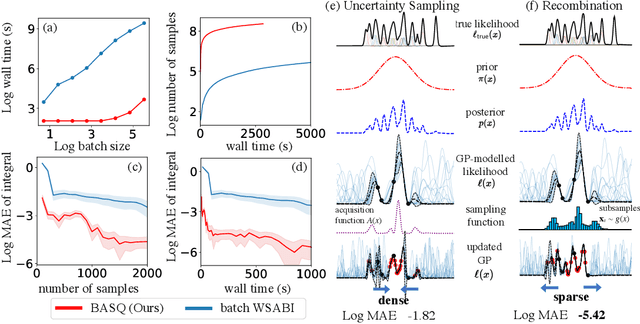
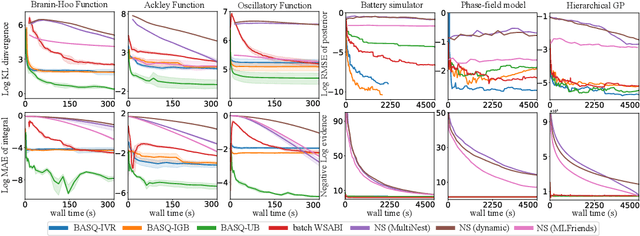
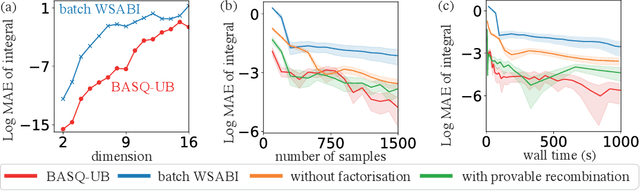
Calculation of Bayesian posteriors and model evidences typically requires numerical integration. Bayesian quadrature (BQ), a surrogate-model-based approach to numerical integration, is capable of superb sample efficiency, but its lack of parallelisation has hindered its practical applications. In this work, we propose a parallelised (batch) BQ method, employing techniques from kernel quadrature, that possesses a provably-exponential convergence rate. Additionally, just as with Nested Sampling, our method permits simultaneous inference of both posteriors and model evidence. Samples from our BQ surrogate model are re-selected to give a sparse set of samples, via a kernel recombination algorithm, requiring negligible additional time to increase the batch size. Empirically, we find that our approach significantly outperforms the sampling efficiency of both state-of-the-art BQ techniques and Nested Sampling in various real-world datasets, including lithium-ion battery analytics.

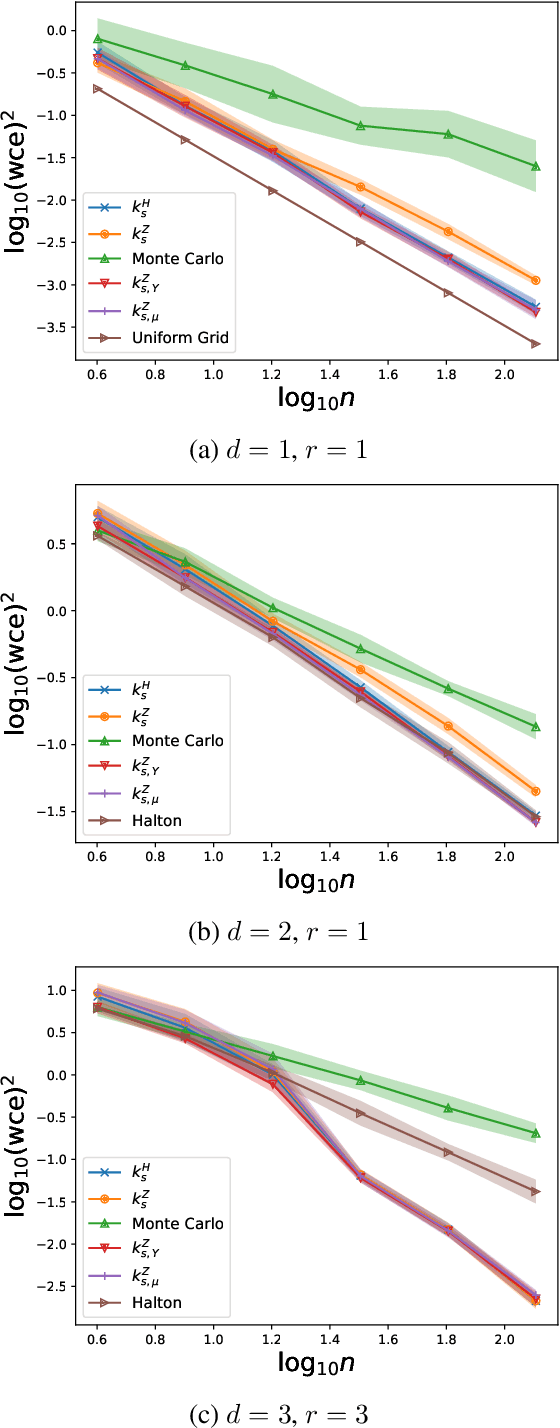
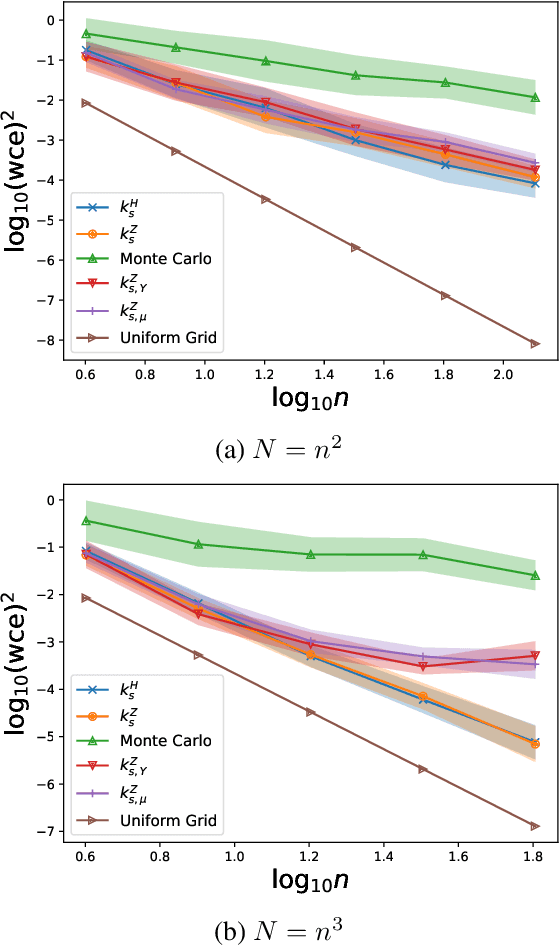
Positively Weighted Kernel Quadrature via Subsampling

We study kernel quadrature rules with positive weights for probability measures on general domains. Our theoretical analysis combines the spectral properties of the kernel with random sampling of points. This results in effective algorithms to construct kernel quadrature rules with positive weights and small worst-case error. Besides additional robustness, our numerical experiments indicate that this can achieve fast convergence rates that compete with the optimal bounds in well-known examples.