Natural Evolutionary Search meets Probabilistic Numerics

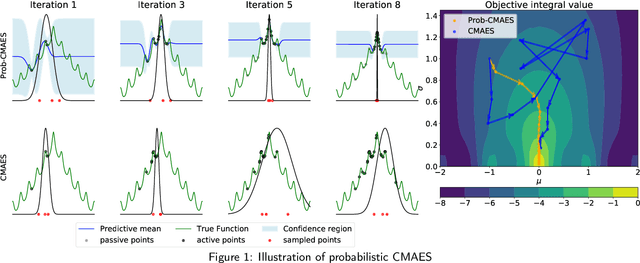
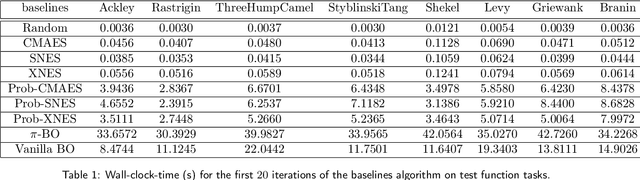
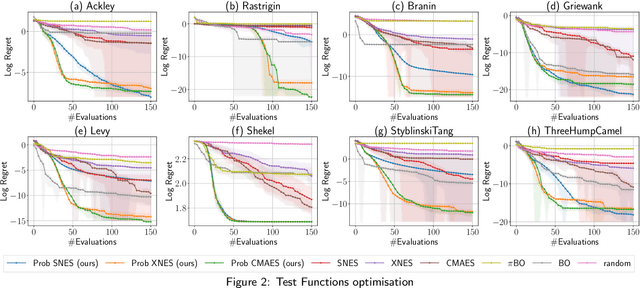
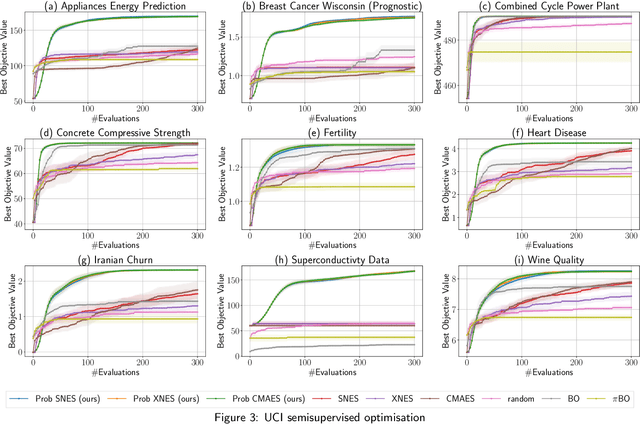
Zeroth-order local optimisation algorithms are essential for solving real-valued black-box optimisation problems. Among these, Natural Evolution Strategies (NES) represent a prominent class, particularly well-suited for scenarios where prior distributions are available. By optimising the objective function in the space of search distributions, NES algorithms naturally integrate prior knowledge during initialisation, making them effective in settings such as semi-supervised learning and user-prior belief frameworks. However, due to their reliance on random sampling and Monte Carlo estimates, NES algorithms can suffer from limited sample efficiency. In this paper, we introduce a novel class of algorithms, termed Probabilistic Natural Evolutionary Strategy Algorithms (ProbNES), which enhance the NES framework with Bayesian quadrature. We show that ProbNES algorithms consistently outperforms their non-probabilistic counterparts as well as global sample efficient methods such as Bayesian Optimisation (BO) or $\pi$BO across a wide range of tasks, including benchmark test functions, data-driven optimisation tasks, user-informed hyperparameter tuning tasks and locomotion tasks.

Scalable Valuation of Human Feedback through Provably Robust Model Alignment

Despite the importance of aligning language models with human preferences, crowd-sourced human feedback is often noisy -- for example, preferring less desirable responses -- posing a fundamental challenge to alignment. A truly robust alignment objective should yield identical model parameters even under severe label noise, a property known as redescending. We prove that no existing alignment methods satisfy this property. To address this, we propose H\"older-DPO, the first principled alignment loss with a provable redescending property, enabling estimation of the clean data distribution from noisy feedback. The aligned model estimates the likelihood of clean data, providing a theoretically grounded metric for dataset valuation that identifies the location and fraction of mislabels. This metric is gradient-free, enabling scalable and automated human feedback valuation without costly manual verification or clean validation dataset. H\"older-DPO achieves state-of-the-art robust alignment performance while accurately detecting mislabels in controlled datasets. Finally, we apply H\"older-DPO to widely used alignment datasets, revealing substantial noise levels and demonstrating that removing these mislabels significantly improves alignment performance across methods.

Fixing the Pitfalls of Probabilistic Time-Series Forecasting Evaluation by Kernel Quadrature

Despite the significance of probabilistic time-series forecasting models, their evaluation metrics often involve intractable integrations. The most widely used metric, the continuous ranked probability score (CRPS), is a strictly proper scoring function; however, its computation requires approximation. We found that popular CRPS estimators--specifically, the quantile-based estimator implemented in the widely used GluonTS library and the probability-weighted moment approximation--both exhibit inherent estimation biases. These biases lead to crude approximations, resulting in improper rankings of forecasting model performance when CRPS values are close. To address this issue, we introduced a kernel quadrature approach that leverages an unbiased CRPS estimator and employs cubature construction for scalable computation. Empirically, our approach consistently outperforms the two widely used CRPS estimators.

Bayesian Optimization for Building Social-Influence-Free Consensus

We introduce Social Bayesian Optimization (SBO), a vote-efficient algorithm for consensus-building in collective decision-making. In contrast to single-agent scenarios, collective decision-making encompasses group dynamics that may distort agents' preference feedback, thereby impeding their capacity to achieve a social-influence-free consensus -- the most preferable decision based on the aggregated agent utilities. We demonstrate that under mild rationality axioms, reaching social-influence-free consensus using noisy feedback alone is impossible. To address this, SBO employs a dual voting system: cheap but noisy public votes (e.g., show of hands in a meeting), and more accurate, though expensive, private votes (e.g., one-to-one interview). We model social influence using an unknown social graph and leverage the dual voting system to efficiently learn this graph. Our theoretical findigns show that social graph estimation converges faster than the black-box estimation of agents' utilities, allowing us to reduce reliance on costly private votes early in the process. This enables efficient consensus-building primarily through noisy public votes, which are debiased based on the estimated social graph to infer social-influence-free feedback. We validate the efficacy of SBO across multiple real-world applications, including thermal comfort, team building, travel negotiation, and energy trading collaboration.

Learning to Forget: Bayesian Time Series Forecasting using Recurrent Sparse Spectrum Signature Gaussian Processes

The signature kernel is a kernel between time series of arbitrary length and comes with strong theoretical guarantees from stochastic analysis. It has found applications in machine learning such as covariance functions for Gaussian processes. A strength of the underlying signature features is that they provide a structured global description of a time series. However, this property can quickly become a curse when local information is essential and forgetting is required; so far this has only been addressed with ad-hoc methods such as slicing the time series into subsegments. To overcome this, we propose a principled, data-driven approach by introducing a novel forgetting mechanism for signatures. This allows the model to dynamically adapt its context length to focus on more recent information. To achieve this, we revisit the recently introduced Random Fourier Signature Features, and develop Random Fourier Decayed Signature Features (RFDSF) with Gaussian processes (GPs). This results in a Bayesian time series forecasting algorithm with variational inference, that offers a scalable probabilistic algorithm that processes and transforms a time series into a joint predictive distribution over time steps in one pass using recurrence. For example, processing a sequence of length $10^4$ steps in $\approx 10^{-2}$ seconds and in $< 1\text{GB}$ of GPU memory. We demonstrate that it outperforms other GP-based alternatives and competes with state-of-the-art probabilistic time series forecasting algorithms.

Principled Bayesian Optimisation in Collaboration with Human Experts

Bayesian optimisation for real-world problems is often performed interactively with human experts, and integrating their domain knowledge is key to accelerate the optimisation process. We consider a setup where experts provide advice on the next query point through binary accept/reject recommendations (labels). Experts' labels are often costly, requiring efficient use of their efforts, and can at the same time be unreliable, requiring careful adjustment of the degree to which any expert is trusted. We introduce the first principled approach that provides two key guarantees. (1) Handover guarantee: similar to a no-regret property, we establish a sublinear bound on the cumulative number of experts' binary labels. Initially, multiple labels per query are needed, but the number of expert labels required asymptotically converges to zero, saving both expert effort and computation time. (2) No-harm guarantee with data-driven trust level adjustment: our adaptive trust level ensures that the convergence rate will not be worse than the one without using advice, even if the advice from experts is adversarial. Unlike existing methods that employ a user-defined function that hand-tunes the trust level adjustment, our approach enables data-driven adjustments. Real-world applications empirically demonstrate that our method not only outperforms existing baselines, but also maintains robustness despite varying labelling accuracy, in tasks of battery design with human experts.

Bayesian Optimisation with Unknown Hyperparameters: Regret Bounds Logarithmically Closer to Optimal

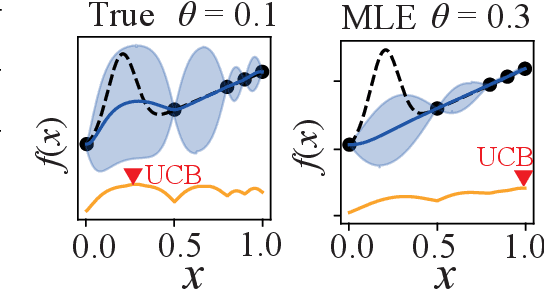
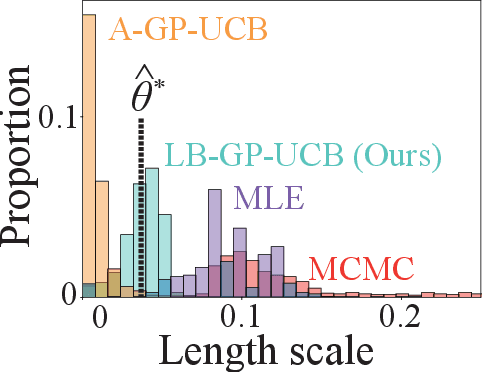
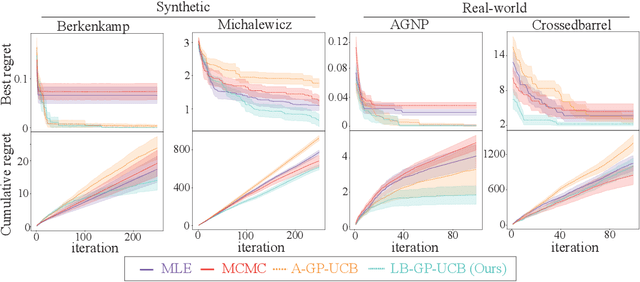
Bayesian Optimization (BO) is widely used for optimising black-box functions but requires us to specify the length scale hyperparameter, which defines the smoothness of the functions the optimizer will consider. Most current BO algorithms choose this hyperparameter by maximizing the marginal likelihood of the observed data, albeit risking misspecification if the objective function is less smooth in regions we have not yet explored. The only prior solution addressing this problem with theoretical guarantees was A-GP-UCB, proposed by Berkenkamp et al. (2019). This algorithm progressively decreases the length scale, expanding the class of functions considered by the optimizer. However, A-GP-UCB lacks a stopping mechanism, leading to over-exploration and slow convergence. To overcome this, we introduce Length scale Balancing (LB) - a novel approach, aggregating multiple base surrogate models with varying length scales. LB intermittently adds smaller length scale candidate values while retaining longer scales, balancing exploration and exploitation. We formally derive a cumulative regret bound of LB and compare it with the regret of an oracle BO algorithm using the optimal length scale. Denoting the factor by which the regret bound of A-GP-UCB was away from oracle as $g(T)$, we show that LB is only $\log g(T)$ away from oracle regret. We also empirically evaluate our algorithm on synthetic and real-world benchmarks and show it outperforms A-GP-UCB, maximum likelihood estimation and MCMC.

A Quadrature Approach for General-Purpose Batch Bayesian Optimization via Probabilistic Lifting

Parallelisation in Bayesian optimisation is a common strategy but faces several challenges: the need for flexibility in acquisition functions and kernel choices, flexibility dealing with discrete and continuous variables simultaneously, model misspecification, and lastly fast massive parallelisation. To address these challenges, we introduce a versatile and modular framework for batch Bayesian optimisation via probabilistic lifting with kernel quadrature, called SOBER, which we present as a Python library based on GPyTorch/BoTorch. Our framework offers the following unique benefits: (1) Versatility in downstream tasks under a unified approach. (2) A gradient-free sampler, which does not require the gradient of acquisition functions, offering domain-agnostic sampling (e.g., discrete and mixed variables, non-Euclidean space). (3) Flexibility in domain prior distribution. (4) Adaptive batch size (autonomous determination of the optimal batch size). (5) Robustness against a misspecified reproducing kernel Hilbert space. (6) Natural stopping criterion.

Beyond Lengthscales: No-regret Bayesian Optimisation With Unknown Hyperparameters Of Any Type

Bayesian optimisation requires fitting a Gaussian process model, which in turn requires specifying hyperparameters - most of the theoretical literature assumes those hyperparameters are known. The commonly used maximum likelihood estimator for hyperparameters of the Gaussian process is consistent only if the data fills the space uniformly, which does not have to be the case in Bayesian optimisation. Since no guarantees exist regarding the correctness of hyperparameter estimation, and those hyperparameters can significantly affect the Gaussian process fit, theoretical analysis of Bayesian optimisation with unknown hyperparameters is very challenging. Previously proposed algorithms with the no-regret property were only able to handle the special case of unknown lengthscales, reproducing kernel Hilbert space norm and applied only to the frequentist case. We propose a novel algorithm, HE-GP-UCB, which is the first algorithm enjoying the no-regret property in the case of unknown hyperparameters of arbitrary form, and which supports both Bayesian and frequentist settings. Our proof idea is novel and can easily be extended to other variants of Bayesian optimisation. We show this by extending our algorithm to the adversarially robust optimisation setting under unknown hyperparameters. Finally, we empirically evaluate our algorithm on a set of toy problems and show that it can outperform the maximum likelihood estimator.

Looping in the Human: Collaborative and Explainable Bayesian Optimization

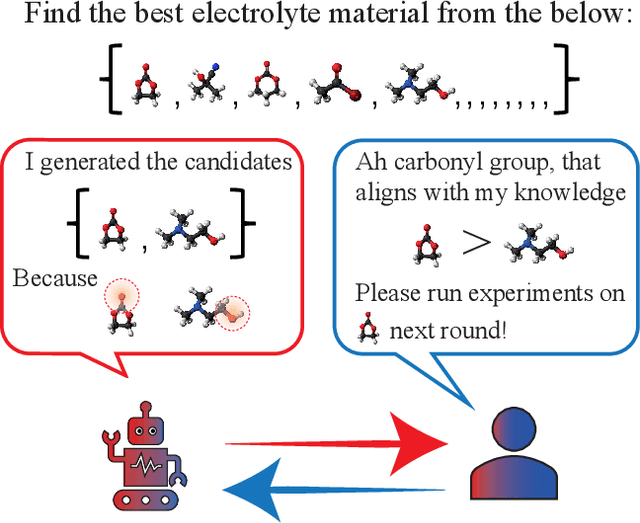
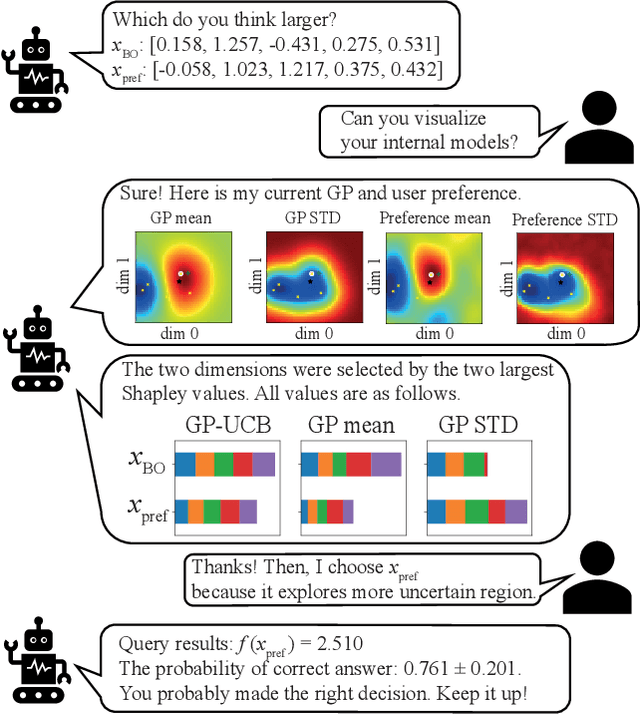
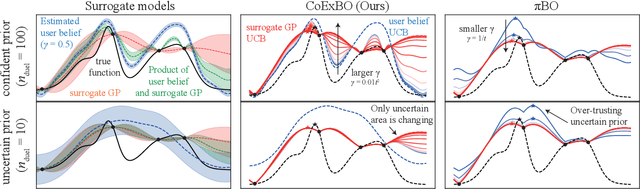
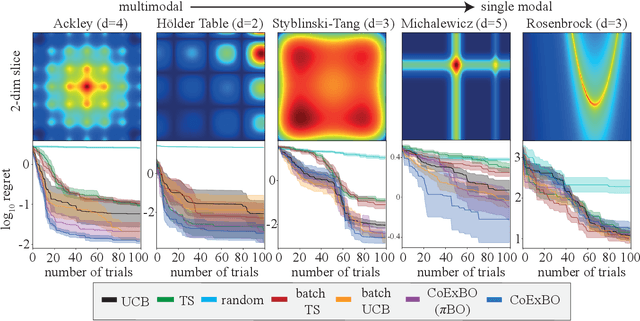
Like many optimizers, Bayesian optimization often falls short of gaining user trust due to opacity. While attempts have been made to develop human-centric optimizers, they typically assume user knowledge is well-specified and error-free, employing users mainly as supervisors of the optimization process. We relax these assumptions and propose a more balanced human-AI partnership with our Collaborative and Explainable Bayesian Optimization (CoExBO) framework. Instead of explicitly requiring a user to provide a knowledge model, CoExBO employs preference learning to seamlessly integrate human insights into the optimization, resulting in algorithmic suggestions that resonate with user preference. CoExBO explains its candidate selection every iteration to foster trust, empowering users with a clearer grasp of the optimization. Furthermore, CoExBO offers a no-harm guarantee, allowing users to make mistakes; even with extreme adversarial interventions, the algorithm converges asymptotically to a vanilla Bayesian optimization. We validate CoExBO's efficacy through human-AI teaming experiments in lithium-ion battery design, highlighting substantial improvements over conventional methods.