Bayesian Optimization for Building Social-Influence-Free Consensus

We introduce Social Bayesian Optimization (SBO), a vote-efficient algorithm for consensus-building in collective decision-making. In contrast to single-agent scenarios, collective decision-making encompasses group dynamics that may distort agents' preference feedback, thereby impeding their capacity to achieve a social-influence-free consensus -- the most preferable decision based on the aggregated agent utilities. We demonstrate that under mild rationality axioms, reaching social-influence-free consensus using noisy feedback alone is impossible. To address this, SBO employs a dual voting system: cheap but noisy public votes (e.g., show of hands in a meeting), and more accurate, though expensive, private votes (e.g., one-to-one interview). We model social influence using an unknown social graph and leverage the dual voting system to efficiently learn this graph. Our theoretical findigns show that social graph estimation converges faster than the black-box estimation of agents' utilities, allowing us to reduce reliance on costly private votes early in the process. This enables efficient consensus-building primarily through noisy public votes, which are debiased based on the estimated social graph to infer social-influence-free feedback. We validate the efficacy of SBO across multiple real-world applications, including thermal comfort, team building, travel negotiation, and energy trading collaboration.

Which price to pay? Auto-tuning building MPC controller for optimal economic cost

Model predictive control (MPC) controller is considered for temperature management in buildings but its performance heavily depends on hyperparameters. Consequently, MPC necessitates meticulous hyperparameter tuning to attain optimal performance under diverse contracts. However, conventional building controller design is an open-loop process without critical hyperparameter optimization, often leading to suboptimal performance due to unexpected environmental disturbances and modeling errors. Furthermore, these hyperparameters are not adapted to different pricing schemes and may lead to non-economic operations. To address these issues, we propose an efficient performance-oriented building MPC controller tuning method based on a cutting-edge efficient constrained Bayesian optimization algorithm, CONFIG, with global optimality guarantees. We demonstrate that this technique can be applied to efficiently deal with real-world DSM program selection problems under customized black-box constraints and objectives. In this study, a simple MPC controller, which offers the advantages of reduced commissioning costs, enhanced computational efficiency, was optimized to perform on a comparable level to a delicately designed and computationally expensive MPC controller. The results also indicate that with an optimized simple MPC, the monthly electricity cost of a household can be reduced by up to 26.90% compared with the cost when controlled by a basic rule-based controller under the same constraints. Then we compared 12 real electricity contracts in Belgium for a household family with customized black-box occupant comfort constraints. The results indicate a monthly electricity bill saving up to 20.18% when the most economic contract is compared with the worst one, which again illustrates the significance of choosing a proper electricity contract.

Principled Bayesian Optimisation in Collaboration with Human Experts

Bayesian optimisation for real-world problems is often performed interactively with human experts, and integrating their domain knowledge is key to accelerate the optimisation process. We consider a setup where experts provide advice on the next query point through binary accept/reject recommendations (labels). Experts' labels are often costly, requiring efficient use of their efforts, and can at the same time be unreliable, requiring careful adjustment of the degree to which any expert is trusted. We introduce the first principled approach that provides two key guarantees. (1) Handover guarantee: similar to a no-regret property, we establish a sublinear bound on the cumulative number of experts' binary labels. Initially, multiple labels per query are needed, but the number of expert labels required asymptotically converges to zero, saving both expert effort and computation time. (2) No-harm guarantee with data-driven trust level adjustment: our adaptive trust level ensures that the convergence rate will not be worse than the one without using advice, even if the advice from experts is adversarial. Unlike existing methods that employ a user-defined function that hand-tunes the trust level adjustment, our approach enables data-driven adjustments. Real-world applications empirically demonstrate that our method not only outperforms existing baselines, but also maintains robustness despite varying labelling accuracy, in tasks of battery design with human experts.

Deja vu: Contrastive Historical Modeling with Prefix-tuning for Temporal Knowledge Graph Reasoning

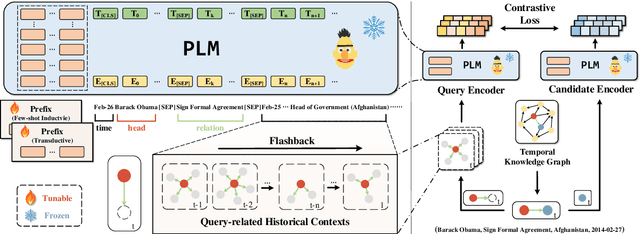
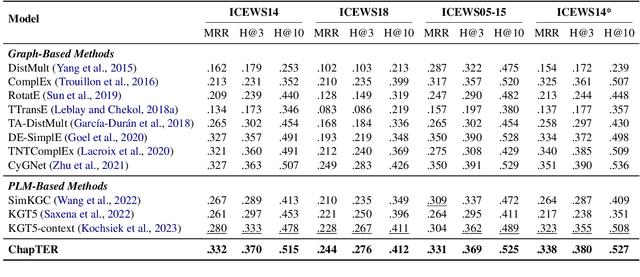
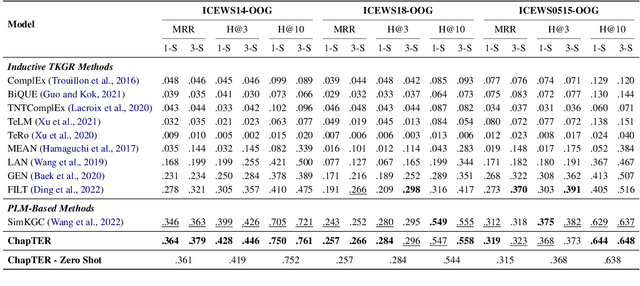
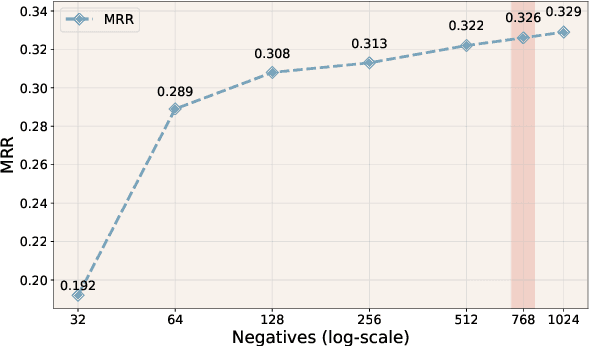
Temporal Knowledge Graph Reasoning (TKGR) is the task of inferring missing facts for incomplete TKGs in complex scenarios (e.g., transductive and inductive settings), which has been gaining increasing attention. Recently, to mitigate dependence on structured connections in TKGs, text-based methods have been developed to utilize rich linguistic information from entity descriptions. However, suffering from the enormous parameters and inflexibility of pre-trained language models, existing text-based methods struggle to balance the textual knowledge and temporal information with computationally expensive purpose-built training strategies. To tap the potential of text-based models for TKGR in various complex scenarios, we propose ChapTER, a Contrastive historical modeling framework with prefix-tuning for TEmporal Reasoning. ChapTER feeds history-contextualized text into the pseudo-Siamese encoders to strike a textual-temporal balance via contrastive estimation between queries and candidates. By introducing virtual time prefix tokens, it applies a prefix-based tuning method to facilitate the frozen PLM capable for TKGR tasks under different settings. We evaluate ChapTER on four transductive and three few-shot inductive TKGR benchmarks, and experimental results demonstrate that ChapTER achieves superior performance compared to competitive baselines with only 0.17% tuned parameters. We conduct thorough analysis to verify the effectiveness, flexibility and efficiency of ChapTER.

Principled Preferential Bayesian Optimization

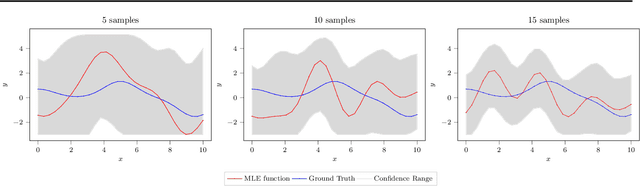
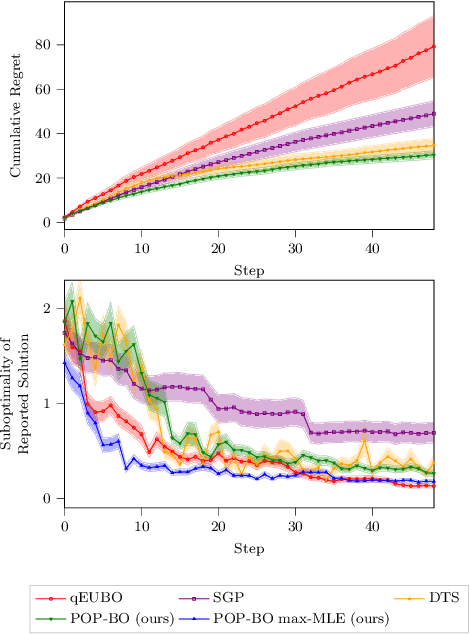
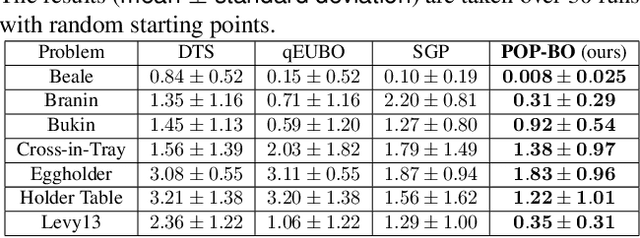
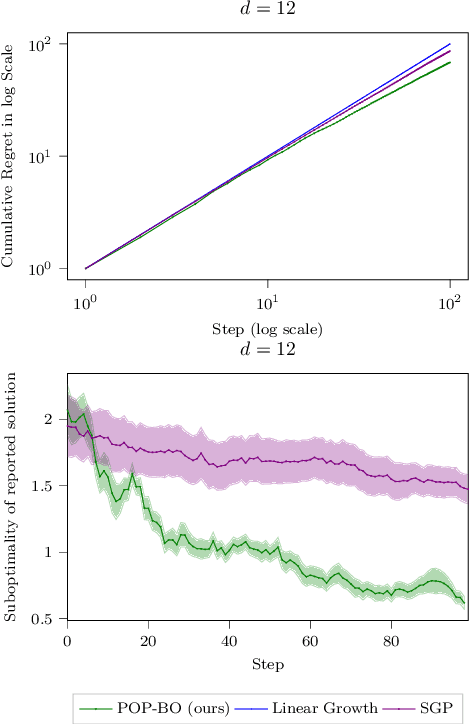
We study the problem of preferential Bayesian optimization (BO), where we aim to optimize a black-box function with only preference feedback over a pair of candidate solutions. Inspired by the likelihood ratio idea, we construct a confidence set of the black-box function using only the preference feedback. An optimistic algorithm with an efficient computational method is then developed to solve the problem, which enjoys an information-theoretic bound on the cumulative regret, a first-of-its-kind for preferential BO. This bound further allows us to design a scheme to report an estimated best solution, with a guaranteed convergence rate. Experimental results on sampled instances from Gaussian processes, standard test functions, and a thermal comfort optimization problem all show that our method stably achieves better or competitive performance as compared to the existing state-of-the-art heuristics, which, however, do not have theoretical guarantees on regret bounds or convergence.

Multi-Agent Bayesian Optimization with Coupled Black-Box and Affine Constraints

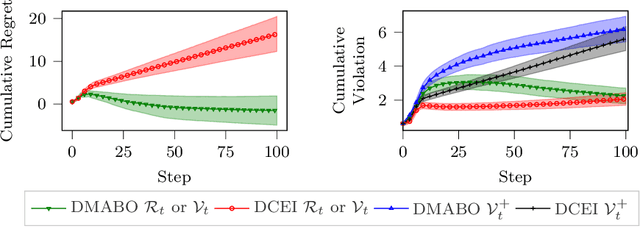
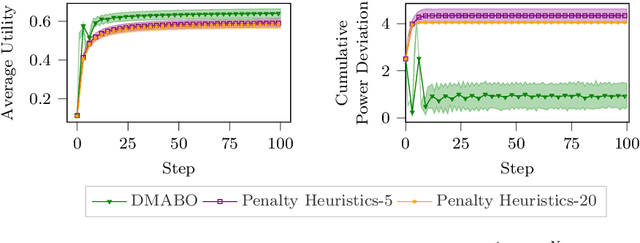
This paper studies the problem of distributed multi-agent Bayesian optimization with both coupled black-box constraints and known affine constraints. A primal-dual distributed algorithm is proposed that achieves similar regret/violation bounds as those in the single-agent case for the black-box objective and constraint functions. Additionally, the algorithm guarantees an $\mathcal{O}(N\sqrt{T})$ bound on the cumulative violation for the known affine constraints, where $N$ is the number of agents. Hence, it is ensured that the average of the samples satisfies the affine constraints up to the error $\mathcal{O}({N}/{\sqrt{T}})$. Furthermore, we characterize certain conditions under which our algorithm can bound a stronger metric of cumulative violation and provide best-iterate convergence without affine constraint. The method is then applied to both sampled instances from Gaussian processes and a real-world optimal power allocation problem for wireless communication; the results show that our method simultaneously provides close-to-optimal performance and maintains minor violations on average, corroborating our theoretical analysis.

Data-driven adaptive building thermal controller tuning with constraints: A primal-dual contextual Bayesian optimization approach

We study the problem of tuning the parameters of a room temperature controller to minimize its energy consumption, subject to the constraint that the daily cumulative thermal discomfort of the occupants is below a given threshold. We formulate it as an online constrained black-box optimization problem where, on each day, we observe some relevant environmental context and adaptively select the controller parameters. In this paper, we propose to use a data-driven Primal-Dual Contextual Bayesian Optimization (PDCBO) approach to solve this problem. In a simulation case study on a single room, we apply our algorithm to tune the parameters of a Proportional Integral (PI) heating controller and the pre-heating time. Our results show that PDCBO can save up to 4.7% energy consumption compared to other state-of-the-art Bayesian optimization-based methods while keeping the daily thermal discomfort below the given tolerable threshold on average. Additionally, PDCBO can automatically track time-varying tolerable thresholds while existing methods fail to do so. We then study an alternative constrained tuning problem where we aim to minimize the thermal discomfort with a given energy budget. With this formulation, PDCBO reduces the average discomfort by up to 63% compared to state-of-the-art safe optimization methods while keeping the average daily energy consumption below the required threshold.

Bayesian Optimization of Expensive Nested Grey-Box Functions

We consider the problem of optimizing a grey-box objective function, i.e., nested function composed of both black-box and white-box functions. A general formulation for such grey-box problems is given, which covers the existing grey-box optimization formulations as special cases. We then design an optimism-driven algorithm to solve it. Under certain regularity assumptions, our algorithm achieves similar regret bound as that for the standard black-box Bayesian optimization algorithm, up to a constant multiplicative term depending on the Lipschitz constants of the functions considered. We further extend our method to the constrained case and discuss several special cases. For the commonly used kernel functions, the regret bounds allow us to derive a convergence rate to the optimal solution. Experimental results show that our grey-box optimization method empirically improves the speed of finding the global optimal solution significantly, as compared to the standard black-box optimization algorithm.

Pre-trained Language Model with Prompts for Temporal Knowledge Graph Completion

Temporal Knowledge graph completion (TKGC) is a crucial task that involves reasoning at known timestamps to complete the missing part of facts and has attracted more and more attention in recent years. Most existing methods focus on learning representations based on graph neural networks while inaccurately extracting information from timestamps and insufficiently utilizing the implied information in relations. To address these problems, we propose a novel TKGC model, namely Pre-trained Language Model with Prompts for TKGC (PPT). We convert a series of sampled quadruples into pre-trained language model inputs and convert intervals between timestamps into different prompts to make coherent sentences with implicit semantic information. We train our model with a masking strategy to convert TKGC task into a masked token prediction task, which can leverage the semantic information in pre-trained language models. Experiments on three benchmark datasets and extensive analysis demonstrate that our model has great competitiveness compared to other models with four metrics. Our model can effectively incorporate information from temporal knowledge graphs into the language models.

Primal-Dual Contextual Bayesian Optimization for Control System Online Optimization with Time-Average Constraints

This paper studies the problem of online performance optimization of constrained closed-loop control systems, where both the objective and the constraints are unknown black-box functions affected by exogenous time-varying contextual disturbances. A primal-dual contextual Bayesian optimization algorithm is proposed that achieves sublinear cumulative regret with respect to the dynamic optimal solution under certain regularity conditions. Furthermore, the algorithm achieves zero time-average constraint violation, ensuring that the average value of the constraint function satisfies the desired constraint. The method is applied to both sampled instances from Gaussian processes and a continuous stirred tank reactor parameter tuning problem; simulation results show that the method simultaneously provides close-to-optimal performance and maintains constraint feasibility on average. This contrasts current state-of-the-art methods, which either suffer from large cumulative regret or severe constraint violations for the case studies presented.