Principled Preferential Bayesian Optimization

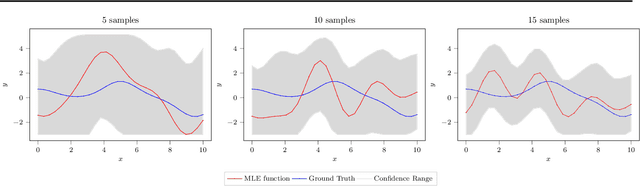
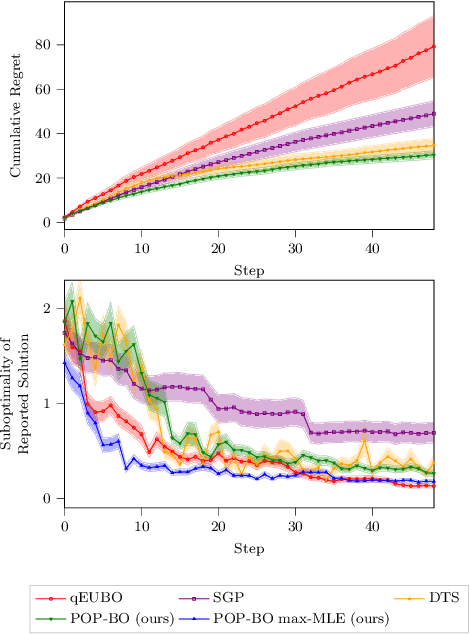
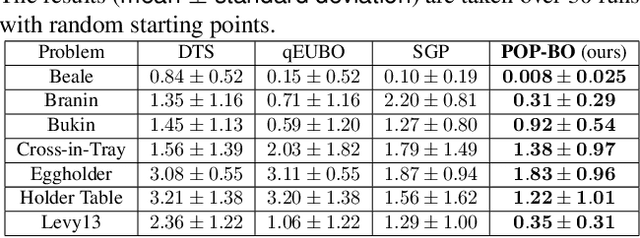
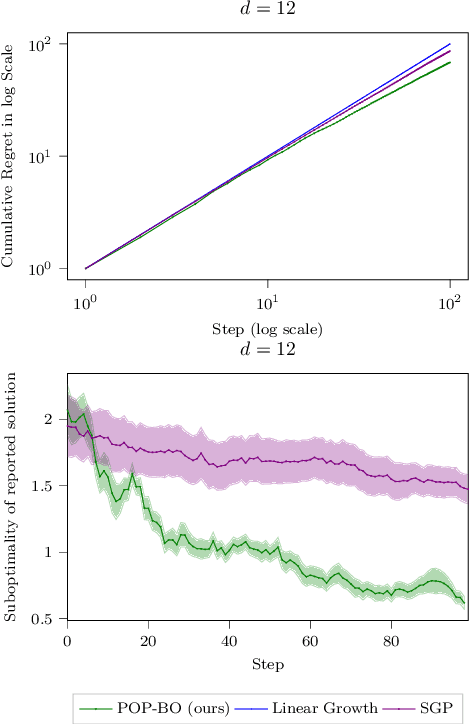
We study the problem of preferential Bayesian optimization (BO), where we aim to optimize a black-box function with only preference feedback over a pair of candidate solutions. Inspired by the likelihood ratio idea, we construct a confidence set of the black-box function using only the preference feedback. An optimistic algorithm with an efficient computational method is then developed to solve the problem, which enjoys an information-theoretic bound on the cumulative regret, a first-of-its-kind for preferential BO. This bound further allows us to design a scheme to report an estimated best solution, with a guaranteed convergence rate. Experimental results on sampled instances from Gaussian processes, standard test functions, and a thermal comfort optimization problem all show that our method stably achieves better or competitive performance as compared to the existing state-of-the-art heuristics, which, however, do not have theoretical guarantees on regret bounds or convergence.

Stable Linear Subspace Identification: A Machine Learning Approach

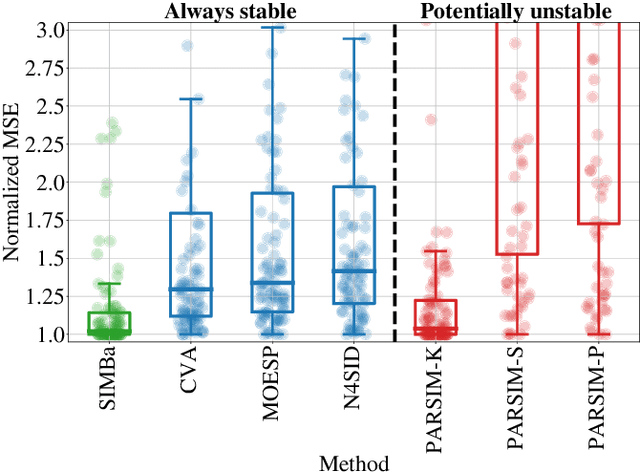
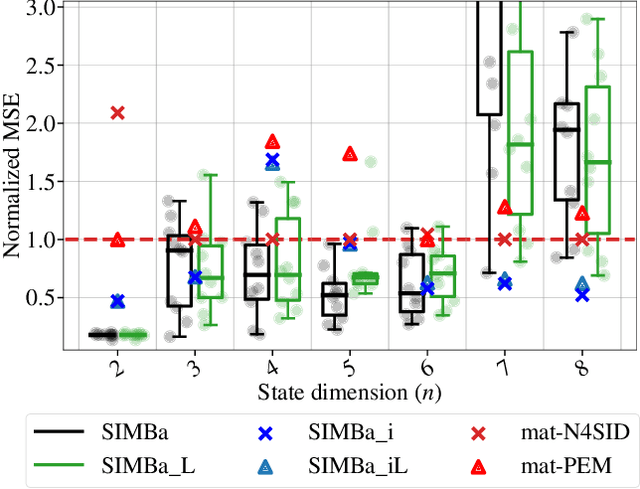
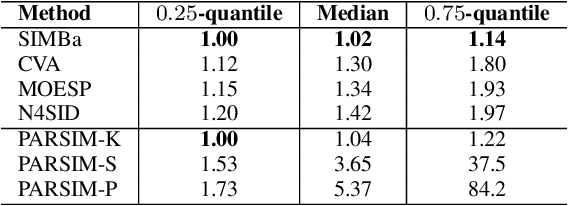
Machine Learning (ML) and linear System Identification (SI) have been historically developed independently. In this paper, we leverage well-established ML tools - especially the automatic differentiation framework - to introduce SIMBa, a family of discrete linear multi-step-ahead state-space SI methods using backpropagation. SIMBa relies on a novel Linear-Matrix-Inequality-based free parametrization of Schur matrices to ensure the stability of the identified model. We show how SIMBa generally outperforms traditional linear state-space SI methods, and sometimes significantly, although at the price of a higher computational burden. This performance gap is particularly remarkable compared to other SI methods with stability guarantees, where the gain is frequently above 25% in our investigations, hinting at SIMBa's ability to simultaneously achieve state-of-the-art fitting performance and enforce stability. Interestingly, these observations hold for a wide variety of input-output systems and on both simulated and real-world data, showcasing the flexibility of the proposed approach. We postulate that this new SI paradigm presents a great extension potential to identify structured nonlinear models from data, and we hence open-source SIMBa on https://github.com/Cemempamoi/simba.

Multi-Agent Bayesian Optimization with Coupled Black-Box and Affine Constraints

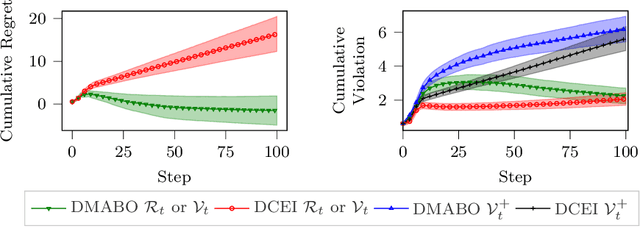
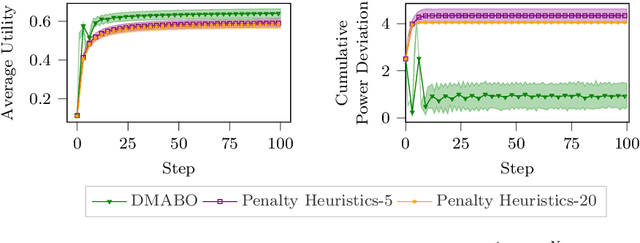
This paper studies the problem of distributed multi-agent Bayesian optimization with both coupled black-box constraints and known affine constraints. A primal-dual distributed algorithm is proposed that achieves similar regret/violation bounds as those in the single-agent case for the black-box objective and constraint functions. Additionally, the algorithm guarantees an $\mathcal{O}(N\sqrt{T})$ bound on the cumulative violation for the known affine constraints, where $N$ is the number of agents. Hence, it is ensured that the average of the samples satisfies the affine constraints up to the error $\mathcal{O}({N}/{\sqrt{T}})$. Furthermore, we characterize certain conditions under which our algorithm can bound a stronger metric of cumulative violation and provide best-iterate convergence without affine constraint. The method is then applied to both sampled instances from Gaussian processes and a real-world optimal power allocation problem for wireless communication; the results show that our method simultaneously provides close-to-optimal performance and maintains minor violations on average, corroborating our theoretical analysis.

Data-driven adaptive building thermal controller tuning with constraints: A primal-dual contextual Bayesian optimization approach

We study the problem of tuning the parameters of a room temperature controller to minimize its energy consumption, subject to the constraint that the daily cumulative thermal discomfort of the occupants is below a given threshold. We formulate it as an online constrained black-box optimization problem where, on each day, we observe some relevant environmental context and adaptively select the controller parameters. In this paper, we propose to use a data-driven Primal-Dual Contextual Bayesian Optimization (PDCBO) approach to solve this problem. In a simulation case study on a single room, we apply our algorithm to tune the parameters of a Proportional Integral (PI) heating controller and the pre-heating time. Our results show that PDCBO can save up to 4.7% energy consumption compared to other state-of-the-art Bayesian optimization-based methods while keeping the daily thermal discomfort below the given tolerable threshold on average. Additionally, PDCBO can automatically track time-varying tolerable thresholds while existing methods fail to do so. We then study an alternative constrained tuning problem where we aim to minimize the thermal discomfort with a given energy budget. With this formulation, PDCBO reduces the average discomfort by up to 63% compared to state-of-the-art safe optimization methods while keeping the average daily energy consumption below the required threshold.

Bayesian Optimization of Expensive Nested Grey-Box Functions

We consider the problem of optimizing a grey-box objective function, i.e., nested function composed of both black-box and white-box functions. A general formulation for such grey-box problems is given, which covers the existing grey-box optimization formulations as special cases. We then design an optimism-driven algorithm to solve it. Under certain regularity assumptions, our algorithm achieves similar regret bound as that for the standard black-box Bayesian optimization algorithm, up to a constant multiplicative term depending on the Lipschitz constants of the functions considered. We further extend our method to the constrained case and discuss several special cases. For the commonly used kernel functions, the regret bounds allow us to derive a convergence rate to the optimal solution. Experimental results show that our grey-box optimization method empirically improves the speed of finding the global optimal solution significantly, as compared to the standard black-box optimization algorithm.

Primal-Dual Contextual Bayesian Optimization for Control System Online Optimization with Time-Average Constraints

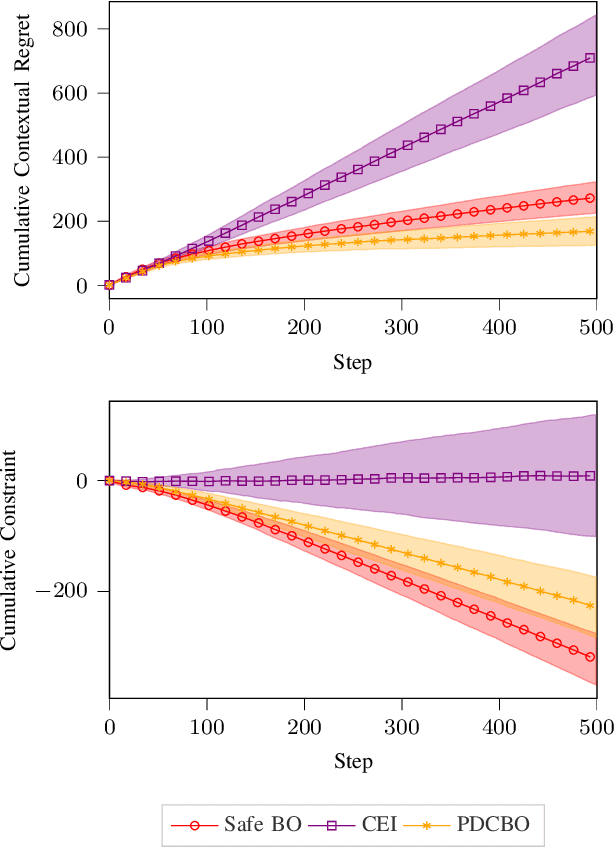
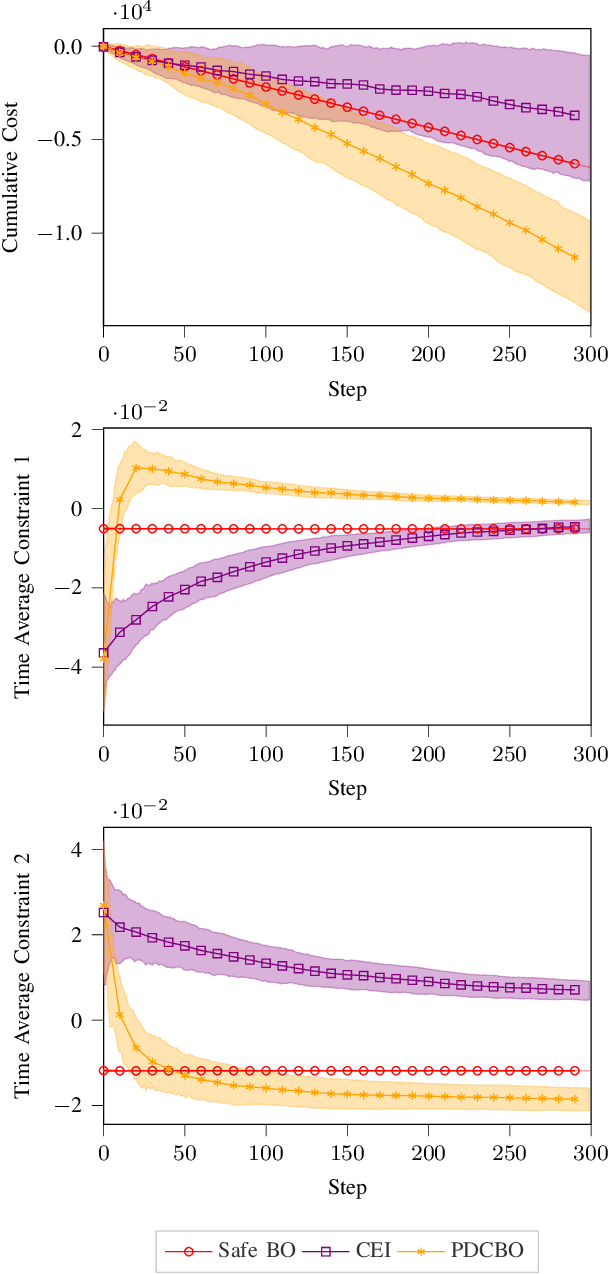
This paper studies the problem of online performance optimization of constrained closed-loop control systems, where both the objective and the constraints are unknown black-box functions affected by exogenous time-varying contextual disturbances. A primal-dual contextual Bayesian optimization algorithm is proposed that achieves sublinear cumulative regret with respect to the dynamic optimal solution under certain regularity conditions. Furthermore, the algorithm achieves zero time-average constraint violation, ensuring that the average value of the constraint function satisfies the desired constraint. The method is applied to both sampled instances from Gaussian processes and a continuous stirred tank reactor parameter tuning problem; simulation results show that the method simultaneously provides close-to-optimal performance and maintains constraint feasibility on average. This contrasts current state-of-the-art methods, which either suffer from large cumulative regret or severe constraint violations for the case studies presented.

Violation-Aware Contextual Bayesian Optimization for Controller Performance Optimization with Unmodeled Constraints

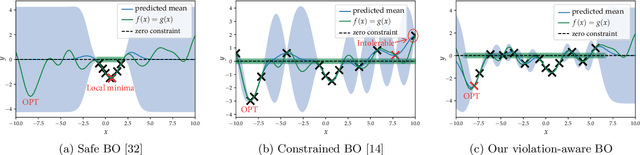
We study the problem of performance optimization of closed-loop control systems with unmodeled dynamics. Bayesian optimization (BO) has been demonstrated to be effective for improving closed-loop performance by automatically tuning controller gains or reference setpoints in a model-free manner. However, BO methods have rarely been tested on dynamical systems with unmodeled constraints and time-varying ambient conditions. In this paper, we propose a violation-aware contextual BO algorithm (VACBO) that optimizes closed-loop performance while simultaneously learning constraint-feasible solutions under time-varying ambient conditions. Unlike classical constrained BO methods which allow unlimited constraint violations, or 'safe' BO algorithms that are conservative and try to operate with near-zero violations, we allow budgeted constraint violations to improve constraint learning and accelerate optimization. We demonstrate the effectiveness of our proposed VACBO method for energy minimization of industrial vapor compression systems under time-varying ambient temperature and humidity.

Towards Scalable Physically Consistent Neural Networks: an Application to Data-driven Multi-zone Thermal Building Models

With more and more data being collected, data-driven modeling methods have been gaining in popularity in recent years. While physically sound, classical gray-box models are often cumbersome to identify and scale, and their accuracy might be hindered by their limited expressiveness. On the other hand, classical black-box methods, typically relying on Neural Networks (NNs) nowadays, often achieve impressive performance, even at scale, by deriving statistical patterns from data. However, they remain completely oblivious to the underlying physical laws, which may lead to potentially catastrophic failures if decisions for real-world physical systems are based on them. Physically Consistent Neural Networks (PCNNs) were recently developed to address these aforementioned issues, ensuring physical consistency while still leveraging NNs to attain state-of-the-art accuracy. In this work, we scale PCNNs to model building temperature dynamics and propose a thorough comparison with classical gray-box and black-box methods. More precisely, we design three distinct PCNN extensions, thereby exemplifying the modularity and flexibility of the architecture, and formally prove their physical consistency. In the presented case study, PCNNs are shown to achieve state-of-the-art accuracy, even outperforming classical NN-based models despite their constrained structure. Our investigations furthermore provide a clear illustration of NNs achieving seemingly good performance while remaining completely physics-agnostic, which can be misleading in practice. While this performance comes at the cost of computational complexity, PCNNs on the other hand show accuracy improvements of 17-35% compared to all other physically consistent methods, paving the way for scalable physically consistent models with state-of-the-art performance.

Efficient Reinforcement Learning (ERL): Targeted Exploration Through Action Saturation

Reinforcement Learning (RL) generally suffers from poor sample complexity, mostly due to the need to exhaustively explore the state space to find good policies. On the other hand, we postulate that expert knowledge of the system to control often allows us to design simple rules we expect good policies to follow at all times. In this work, we hence propose a simple yet effective modification of continuous actor-critic RL frameworks to incorporate such prior knowledge in the learned policies and constrain them to regions of the state space that are deemed interesting, thereby significantly accelerating their convergence. Concretely, we saturate the actions chosen by the agent if they do not comply with our intuition and, critically, modify the gradient update step of the policy to ensure the learning process does not suffer from the saturation step. On a room temperature control simulation case study, these modifications allow agents to converge to well-performing policies up to one order of magnitude faster than classical RL agents while retaining good final performance.

CONFIG: Constrained Efficient Global Optimization for Closed-Loop Control System Optimization with Unmodeled Constraints

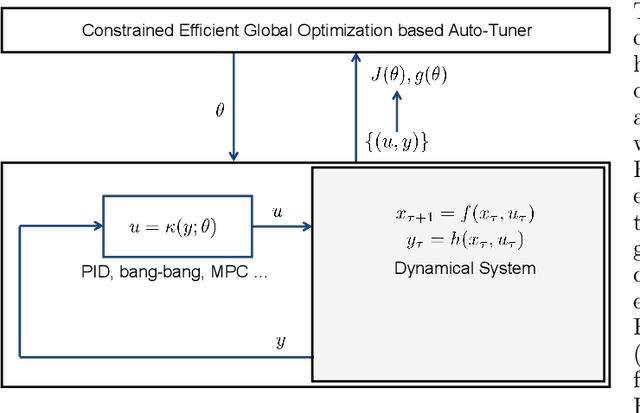
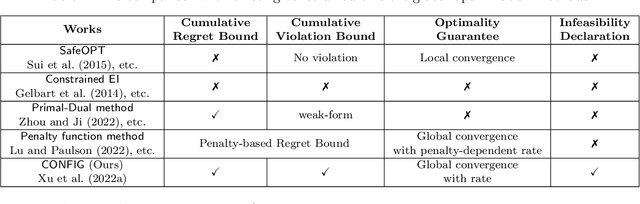
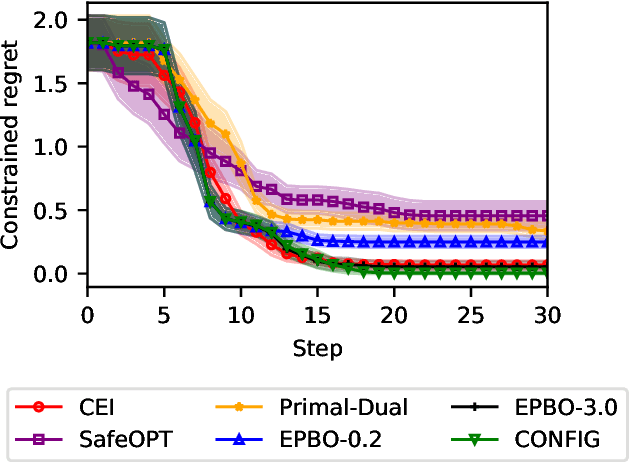
In this paper, the CONFIG algorithm, a simple and provably efficient constrained global optimization algorithm, is applied to optimize the closed-loop control performance of an unknown system with unmodeled constraints. Existing Gaussian process based closed-loop optimization methods, either can only guarantee local convergence (e.g., SafeOPT), or have no known optimality guarantee (e.g., constrained expected improvement) at all, whereas the recently introduced CONFIG algorithm has been proven to enjoy a theoretical global optimality guarantee. In this study, we demonstrate the effectiveness of CONFIG algorithm in the applications. The algorithm is first applied to an artificial numerical benchmark problem to corroborate its effectiveness. It is then applied to a classical constrained steady-state optimization problem of a continuous stirred-tank reactor. Simulation results show that our CONFIG algorithm can achieve performance competitive with the popular CEI (Constrained Expected Improvement) algorithm, which has no known optimality guarantee. As such, the CONFIG algorithm offers a new tool, with both a provable global optimality guarantee and competitive empirical performance, to optimize the closed-loop control performance for a system with soft unmodeled constraints. Last, but not least, the open-source code is available as a python package to facilitate future applications.