Personalized Federated Learning of Probabilistic Models: A PAC-Bayesian Approach

Federated learning aims to infer a shared model from private and decentralized data stored locally by multiple clients. Personalized federated learning (PFL) goes one step further by adapting the global model to each client, enhancing the model's fit for different clients. A significant level of personalization is required for highly heterogeneous clients, but can be challenging to achieve especially when they have small datasets. To address this problem, we propose a PFL algorithm named PAC-PFL for learning probabilistic models within a PAC-Bayesian framework that utilizes differential privacy to handle data-dependent priors. Our algorithm collaboratively learns a shared hyper-posterior and regards each client's posterior inference as the personalization step. By establishing and minimizing a generalization bound on the average true risk of clients, PAC-PFL effectively combats over-fitting. PACPFL achieves accurate and well-calibrated predictions, supported by experiments on a dataset of photovoltaic panel power generation, FEMNIST dataset (Caldas et al., 2019), and Dirichlet-partitioned EMNIST dataset (Cohen et al., 2017).

Stable Linear Subspace Identification: A Machine Learning Approach

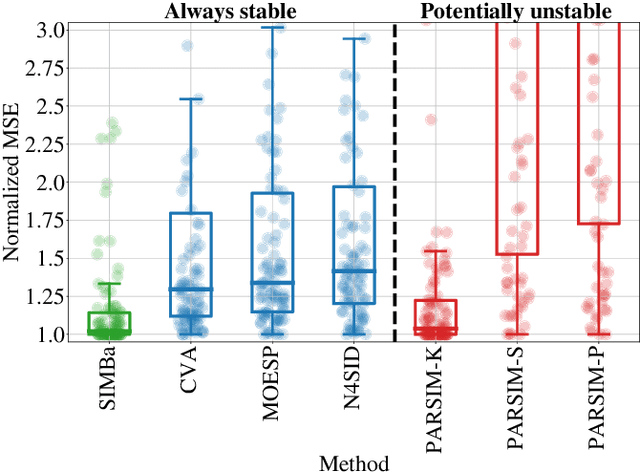
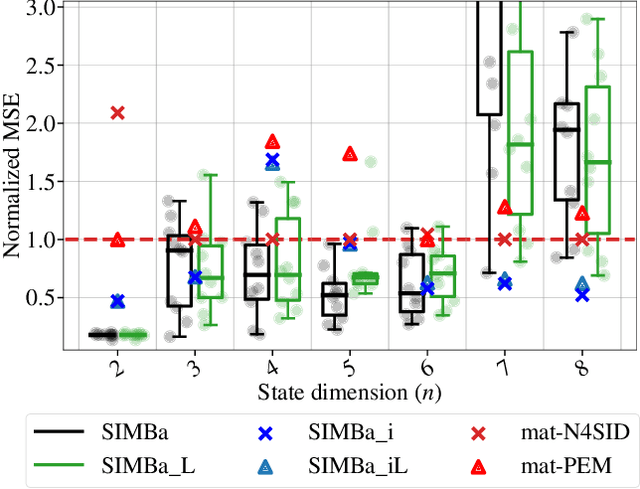
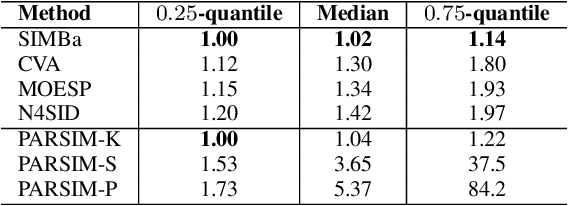
Machine Learning (ML) and linear System Identification (SI) have been historically developed independently. In this paper, we leverage well-established ML tools - especially the automatic differentiation framework - to introduce SIMBa, a family of discrete linear multi-step-ahead state-space SI methods using backpropagation. SIMBa relies on a novel Linear-Matrix-Inequality-based free parametrization of Schur matrices to ensure the stability of the identified model. We show how SIMBa generally outperforms traditional linear state-space SI methods, and sometimes significantly, although at the price of a higher computational burden. This performance gap is particularly remarkable compared to other SI methods with stability guarantees, where the gain is frequently above 25% in our investigations, hinting at SIMBa's ability to simultaneously achieve state-of-the-art fitting performance and enforce stability. Interestingly, these observations hold for a wide variety of input-output systems and on both simulated and real-world data, showcasing the flexibility of the proposed approach. We postulate that this new SI paradigm presents a great extension potential to identify structured nonlinear models from data, and we hence open-source SIMBa on https://github.com/Cemempamoi/simba.

Physically Consistent Neural ODEs for Learning Multi-Physics Systems

Despite the immense success of neural networks in modeling system dynamics from data, they often remain physics-agnostic black boxes. In the particular case of physical systems, they might consequently make physically inconsistent predictions, which makes them unreliable in practice. In this paper, we leverage the framework of Irreversible port-Hamiltonian Systems (IPHS), which can describe most multi-physics systems, and rely on Neural Ordinary Differential Equations (NODEs) to learn their parameters from data. Since IPHS models are consistent with the first and second principles of thermodynamics by design, so are the proposed Physically Consistent NODEs (PC-NODEs). Furthermore, the NODE training procedure allows us to seamlessly incorporate prior knowledge of the system properties in the learned dynamics. We demonstrate the effectiveness of the proposed method by learning the thermodynamics of a building from the real-world measurements and the dynamics of a simulated gas-piston system. Thanks to the modularity and flexibility of the IPHS framework, PC-NODEs can be extended to learn physically consistent models of multi-physics distributed systems.

A unified framework for Hamiltonian deep neural networks

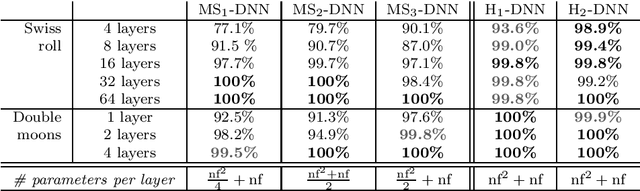
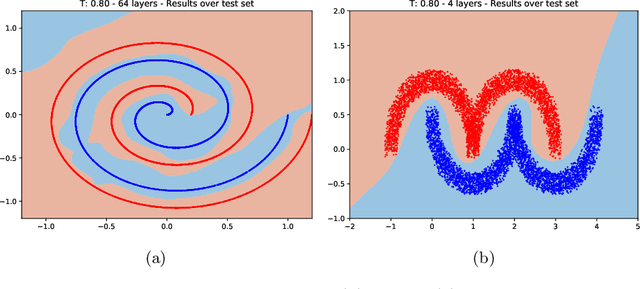
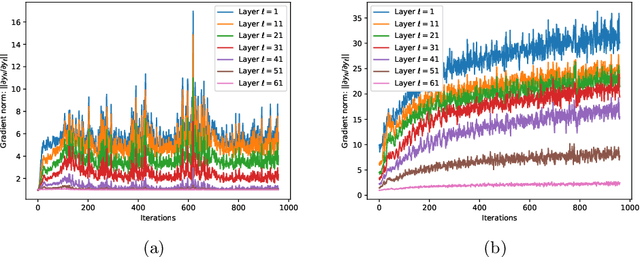
Training deep neural networks (DNNs) can be difficult due to the occurrence of vanishing/exploding gradients during weight optimization. To avoid this problem, we propose a class of DNNs stemming from the time discretization of Hamiltonian systems. The time-invariant version of the corresponding Hamiltonian models enjoys marginal stability, a property that, as shown in previous works and for specific DNNs architectures, can mitigate convergence to zero or divergence of gradients. In the present paper, we formally study this feature by deriving and analysing the backward gradient dynamics in continuous time. The proposed Hamiltonian framework, besides encompassing existing networks inspired by marginally stable ODEs, allows one to derive new and more expressive architectures. The good performance of the novel DNNs is demonstrated on benchmark classification problems, including digit recognition using the MNIST dataset.