Stability-Preserving Online Adaptation of Neural Closed-loop Maps

The growing complexity of modern control tasks calls for controllers that can react online as objectives and disturbances change, while preserving closed-loop stability. Recent approaches for improving the performance of nonlinear systems while preserving closed-loop stability rely on time-invariant recurrent neural-network controllers, but offer no principled way to update the controller during operation. Most importantly, switching from one stabilizing policy to another can itself destabilize the closed-loop. We address this problem by introducing a stability-preserving update mechanism for nonlinear, neural-network-based controllers. Each controller is modeled as a causal operator with bounded $\ell_p$-gain, and we derive gain-based conditions under which the controller may be updated online. These conditions yield two practical update schemes, time-scheduled and state-triggered, that guarantee the closed-loop remains $\ell_p$-stable after any number of updates. Our analysis further shows that stability is decoupled from controller optimality, allowing approximate or early-stopped controller synthesis. We demonstrate the approach on nonlinear systems with time-varying objectives and disturbances, and show consistent performance improvements over static and naive online baselines while guaranteeing stability.

Scaling up Stability: Reinforcement Learning for Distributed Control of Networked Systems in the Space of Stabilizing Policies

We study distributed control of networked systems through reinforcement learning, where neural policies must be simultaneously scalable, expressive and stabilizing. We introduce a policy parameterization that embeds Graph Neural Networks (GNNs) into a Youla-like magnitude-direction parameterization, yielding distributed stochastic controllers that guarantee network-level closed-loop stability by design. The magnitude is implemented as a stable operator consisting of a GNN acting on disturbance feedback, while the direction is a GNN acting on local observations. We prove robustness of the closed loop to perturbations in both the graph topology and model parameters, and show how to integrate our parameterization with Proximal Policy Optimization. Experiments on a multi-agent navigation task show that policies trained on small networks transfer directly to larger ones and unseen network topologies, achieve higher returns and lower variance than a state-of-the-art MARL baseline while preserving stability.

Learning to optimize with guarantees: a complete characterization of linearly convergent algorithms

In high-stakes engineering applications, optimization algorithms must come with provable worst-case guarantees over a mathematically defined class of problems. Designing for the worst case, however, inevitably sacrifices performance on the specific problem instances that often occur in practice. We address the problem of augmenting a given linearly convergent algorithm to improve its average-case performance on a restricted set of target problems - for example, tailoring an off-the-shelf solver for model predictive control (MPC) for an application to a specific dynamical system - while preserving its worst-case guarantees across the entire problem class. Toward this goal, we characterize the class of algorithms that achieve linear convergence for classes of nonsmooth composite optimization problems. In particular, starting from a baseline linearly convergent algorithm, we derive all - and only - the modifications to its update rule that maintain its convergence properties. Our results apply to augmenting legacy algorithms such as gradient descent for nonconvex, gradient-dominated functions; Nesterov's accelerated method for strongly convex functions; and projected methods for optimization over polyhedral feasibility sets. We showcase effectiveness of the approach on solving optimization problems with tight iteration budgets in application to ill-conditioned systems of linear equations and MPC for linear systems.

MAD: A Magnitude And Direction Policy Parametrization for Stability Constrained Reinforcement Learning

We introduce magnitude and direction (MAD) policies, a policy parameterization for reinforcement learning (RL) that preserves Lp closed-loop stability for nonlinear dynamical systems. Although complete in their ability to describe all stabilizing controllers, methods based on nonlinear Youla and system-level synthesis are significantly affected by the difficulty of parameterizing Lp-stable operators. In contrast, MAD policies introduce explicit feedback on state-dependent features - a key element behind the success of RL pipelines - without compromising closed-loop stability. This is achieved by describing the magnitude of the control input with a disturbance-feedback Lp-stable operator, while selecting its direction based on state-dependent features through a universal function approximator. We further characterize the robust stability properties of MAD policies under model mismatch. Unlike existing disturbance-feedback policy parameterizations, MAD policies introduce state-feedback components compatible with model-free RL pipelines, ensuring closed-loop stability without requiring model information beyond open-loop stability. Numerical experiments show that MAD policies trained with deep deterministic policy gradient (DDPG) methods generalize to unseen scenarios, matching the performance of standard neural network policies while guaranteeing closed-loop stability by design.

Learning to Boost the Performance of Stable Nonlinear Systems

The growing scale and complexity of safety-critical control systems underscore the need to evolve current control architectures aiming for the unparalleled performances achievable through state-of-the-art optimization and machine learning algorithms. However, maintaining closed-loop stability while boosting the performance of nonlinear control systems using data-driven and deep-learning approaches stands as an important unsolved challenge. In this paper, we tackle the performance-boosting problem with closed-loop stability guarantees. Specifically, we establish a synergy between the Internal Model Control (IMC) principle for nonlinear systems and state-of-the-art unconstrained optimization approaches for learning stable dynamics. Our methods enable learning over arbitrarily deep neural network classes of performance-boosting controllers for stable nonlinear systems; crucially, we guarantee Lp closed-loop stability even if optimization is halted prematurely, and even when the ground-truth dynamics are unknown, with vanishing conservatism in the class of stabilizing policies as the model uncertainty is reduced to zero. We discuss the implementation details of the proposed control schemes, including distributed ones, along with the corresponding optimization procedures, demonstrating the potential of freely shaping the cost functions through several numerical experiments.

Learning to optimize with convergence guarantees using nonlinear system theory

The increasing reliance on numerical methods for controlling dynamical systems and training machine learning models underscores the need to devise algorithms that dependably and efficiently navigate complex optimization landscapes. Classical gradient descent methods offer strong theoretical guarantees for convex problems; however, they demand meticulous hyperparameter tuning for non-convex ones. The emerging paradigm of learning to optimize (L2O) automates the discovery of algorithms with optimized performance leveraging learning models and data - yet, it lacks a theoretical framework to analyze convergence and robustness of the learned algorithms. In this paper, we fill this gap by harnessing nonlinear system theory. Specifically, we propose an unconstrained parametrization of all convergent algorithms for smooth non-convex objective functions. Notably, our framework is directly compatible with automatic differentiation tools, ensuring convergence by design while learning to optimize.

Unconstrained Parametrization of Dissipative and Contracting Neural Ordinary Differential Equations

In this work, we introduce and study a class of Deep Neural Networks (DNNs) in continuous-time. The proposed architecture stems from the combination of Neural Ordinary Differential Equations (Neural ODEs) with the model structure of recently introduced Recurrent Equilibrium Networks (RENs). We show how to endow our proposed NodeRENs with contractivity and dissipativity -- crucial properties for robust learning and control. Most importantly, as for RENs, we derive parametrizations of contractive and dissipative NodeRENs which are unconstrained, hence enabling their learning for a large number of parameters. We validate the properties of NodeRENs, including the possibility of handling irregularly sampled data, in a case study in nonlinear system identification.

Follow the Clairvoyant: an Imitation Learning Approach to Optimal Control

We consider control of dynamical systems through the lens of competitive analysis. Most prior work in this area focuses on minimizing regret, that is, the loss relative to an ideal clairvoyant policy that has noncausal access to past, present, and future disturbances. Motivated by the observation that the optimal cost only provides coarse information about the ideal closed-loop behavior, we instead propose directly minimizing the tracking error relative to the optimal trajectories in hindsight, i.e., imitating the clairvoyant policy. By embracing a system level perspective, we present an efficient optimization-based approach for computing follow-the-clairvoyant (FTC) safe controllers. We prove that these attain minimal regret if no constraints are imposed on the noncausal benchmark. In addition, we present numerical experiments to show that our policy retains the hallmark of competitive algorithms of interpolating between classical $\mathcal{H}_2$ and $\mathcal{H}_\infty$ control laws - while consistently outperforming regret minimization methods in constrained scenarios thanks to the superior ability to chase the clairvoyant.

Neural System Level Synthesis: Learning over All Stabilizing Policies for Nonlinear Systems

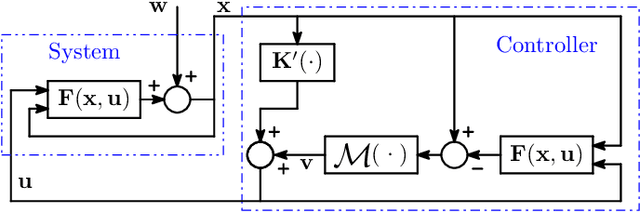
We address the problem of designing stabilizing control policies for nonlinear systems in discrete-time, while minimizing an arbitrary cost function. When the system is linear and the cost is convex, the System Level Synthesis (SLS) approach offers an exact solution based on convex programming. Beyond this case, a globally optimal solution cannot be found in a tractable way, in general. In this paper, we develop a parametrization of all and only the control policies stabilizing a given time-varying nonlinear system in terms of the combined effect of 1) a strongly stabilizing base controller and 2) a stable SLS operator to be freely designed. Based on this result, we propose a Neural SLS (Neur-SLS) approach guaranteeing closed-loop stability during and after parameter optimization, without requiring any constraints to be satisfied. We exploit recent Deep Neural Network (DNN) models based on Recurrent Equilibrium Networks (RENs) to learn over a rich class of nonlinear stable operators, and demonstrate the effectiveness of the proposed approach in numerical examples.

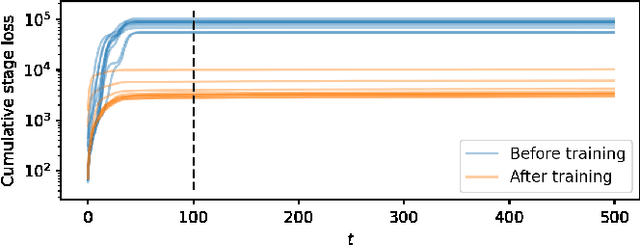
Distributed neural network control with dependability guarantees: a compositional port-Hamiltonian approach

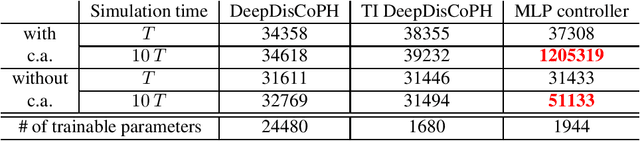
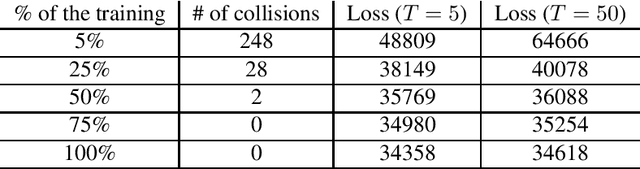
Large-scale cyber-physical systems require that control policies are distributed, that is, that they only rely on local real-time measurements and communication with neighboring agents. Optimal Distributed Control (ODC) problems are, however, highly intractable even in seemingly simple cases. Recent work has thus proposed training Neural Network (NN) distributed controllers. A main challenge of NN controllers is that they are not dependable during and after training, that is, the closed-loop system may be unstable, and the training may fail due to vanishing and exploding gradients. In this paper, we address these issues for networks of nonlinear port-Hamiltonian (pH) systems, whose modeling power ranges from energy systems to non-holonomic vehicles and chemical reactions. Specifically, we embrace the compositional properties of pH systems to characterize deep Hamiltonian control policies with built-in closed-loop stability guarantees, irrespective of the interconnection topology and the chosen NN parameters. Furthermore, our setup enables leveraging recent results on well-behaved neural ODEs to prevent the phenomenon of vanishing gradients by design. Numerical experiments corroborate the dependability of the proposed architecture, while matching the performance of general neural network policies.