Neural Port-Hamiltonian Models for Nonlinear Distributed Control: An Unconstrained Parametrization Approach

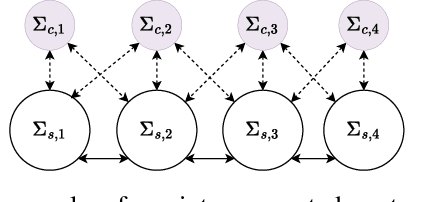
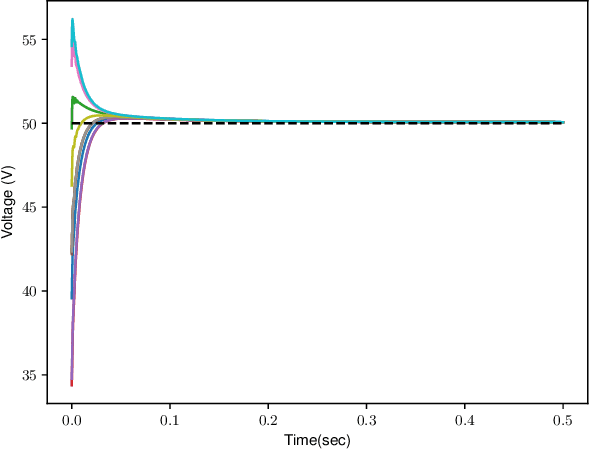
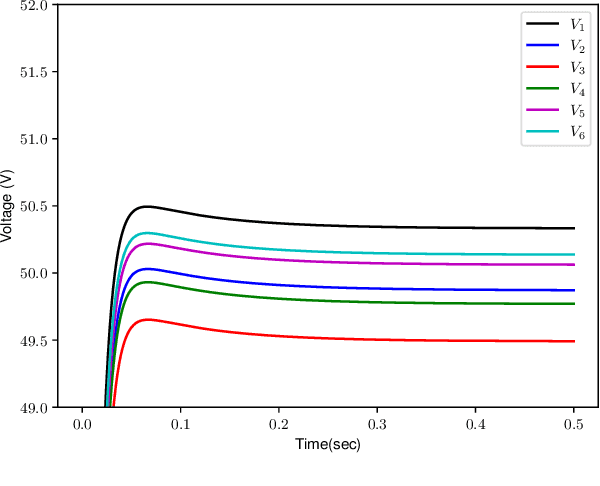
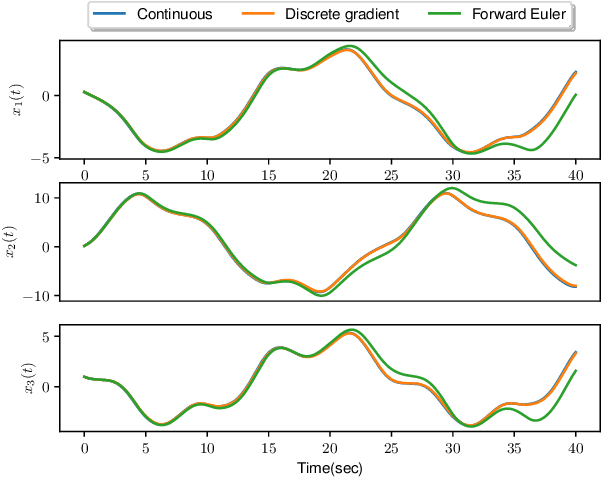
The control of large-scale cyber-physical systems requires optimal distributed policies relying solely on limited communication with neighboring agents. However, computing stabilizing controllers for nonlinear systems while optimizing complex costs remains a significant challenge. Neural Networks (NNs), known for their expressivity, can be leveraged to parametrize control policies that yield good performance. However, NNs' sensitivity to small input changes poses a risk of destabilizing the closed-loop system. Many existing approaches enforce constraints on the controllers' parameter space to guarantee closed-loop stability, leading to computationally expensive optimization procedures. To address these problems, we leverage the framework of port-Hamiltonian systems to design continuous-time distributed control policies for nonlinear systems that guarantee closed-loop stability and finite $\mathcal{L}_2$ or incremental $\mathcal{L}_2$ gains, independent of the optimzation parameters of the controllers. This eliminates the need to constrain parameters during optimization, allowing the use of standard techniques such as gradient-based methods. Additionally, we discuss discretization schemes that preserve the dissipation properties of these controllers for implementation on embedded systems. The effectiveness of the proposed distributed controllers is demonstrated through consensus control of non-holonomic mobile robots subject to collision avoidance and averaged voltage regulation with weighted power sharing in DC microgrids.

Stable Linear Subspace Identification: A Machine Learning Approach

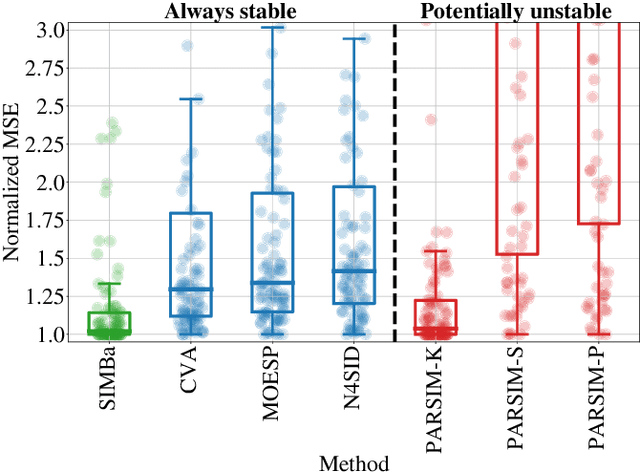
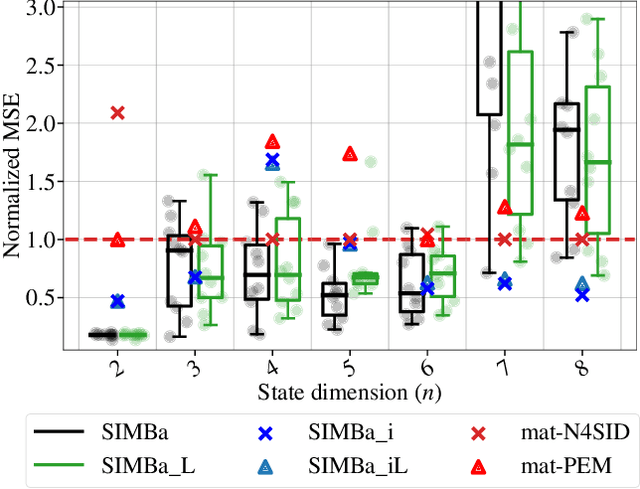
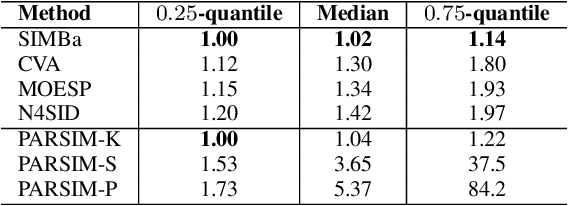
Machine Learning (ML) and linear System Identification (SI) have been historically developed independently. In this paper, we leverage well-established ML tools - especially the automatic differentiation framework - to introduce SIMBa, a family of discrete linear multi-step-ahead state-space SI methods using backpropagation. SIMBa relies on a novel Linear-Matrix-Inequality-based free parametrization of Schur matrices to ensure the stability of the identified model. We show how SIMBa generally outperforms traditional linear state-space SI methods, and sometimes significantly, although at the price of a higher computational burden. This performance gap is particularly remarkable compared to other SI methods with stability guarantees, where the gain is frequently above 25% in our investigations, hinting at SIMBa's ability to simultaneously achieve state-of-the-art fitting performance and enforce stability. Interestingly, these observations hold for a wide variety of input-output systems and on both simulated and real-world data, showcasing the flexibility of the proposed approach. We postulate that this new SI paradigm presents a great extension potential to identify structured nonlinear models from data, and we hence open-source SIMBa on https://github.com/Cemempamoi/simba.

Modulation Classification Through Deep Learning Using Resolution Transformed Spectrograms

Modulation classification is an essential step of signal processing and has been regularly applied in the field of tele-communication. Since variations of frequency with respect to time remains a vital distinction among radio signals having different modulation formats, these variations can be used for feature extraction by converting 1-D radio signals into frequency domain. In this paper, we propose a scheme for Automatic Modulation Classification (AMC) using modern architectures of Convolutional Neural Networks (CNN), through generating spectrum images of eleven different modulation types. Additionally, we perform resolution transformation of spectrograms that results up to 99.61% of computational load reduction and 8x faster conversion from the received I/Q data. This proposed AMC is implemented on CPU and GPU, to recognize digital as well as analogue signal modulation schemes on signals. The performance is evaluated on existing CNN models including SqueezeNet, Resnet-50, InceptionResnet-V2, Inception-V3, VGG-16 and Densenet-201. Best results of 91.2% are achieved in presence of AWGN and other noise impairments in the signals, stating that the transformed spectrogram-based AMC has good classification accuracy as the spectral features are highly discriminant, and CNN based models have capability to extract these high-dimensional features. The spectrograms were created under different SNRs ranging from 5 to 30db with a step size of 5db to observe the experimental results at various SNR levels. The proposed methodology is efficient to be applied in wireless communication networks for real-time applications.

Universal Approximation Property of Hamiltonian Deep Neural Networks

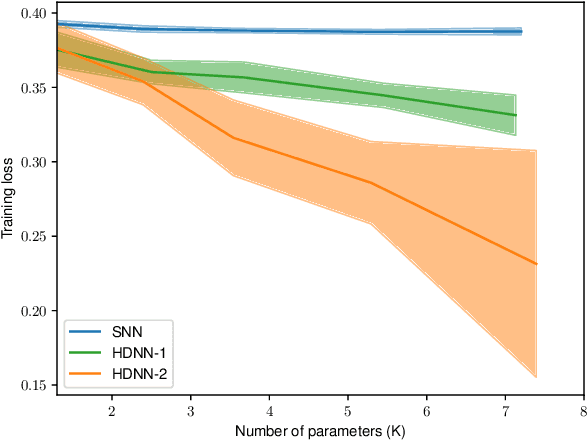
This paper investigates the universal approximation capabilities of Hamiltonian Deep Neural Networks (HDNNs) that arise from the discretization of Hamiltonian Neural Ordinary Differential Equations. Recently, it has been shown that HDNNs enjoy, by design, non-vanishing gradients, which provide numerical stability during training. However, although HDNNs have demonstrated state-of-the-art performance in several applications, a comprehensive study to quantify their expressivity is missing. In this regard, we provide a universal approximation theorem for HDNNs and prove that a portion of the flow of HDNNs can approximate arbitrary well any continuous function over a compact domain. This result provides a solid theoretical foundation for the practical use of HDNNs.

Physically Consistent Neural ODEs for Learning Multi-Physics Systems

Despite the immense success of neural networks in modeling system dynamics from data, they often remain physics-agnostic black boxes. In the particular case of physical systems, they might consequently make physically inconsistent predictions, which makes them unreliable in practice. In this paper, we leverage the framework of Irreversible port-Hamiltonian Systems (IPHS), which can describe most multi-physics systems, and rely on Neural Ordinary Differential Equations (NODEs) to learn their parameters from data. Since IPHS models are consistent with the first and second principles of thermodynamics by design, so are the proposed Physically Consistent NODEs (PC-NODEs). Furthermore, the NODE training procedure allows us to seamlessly incorporate prior knowledge of the system properties in the learned dynamics. We demonstrate the effectiveness of the proposed method by learning the thermodynamics of a building from the real-world measurements and the dynamics of a simulated gas-piston system. Thanks to the modularity and flexibility of the IPHS framework, PC-NODEs can be extended to learn physically consistent models of multi-physics distributed systems.

On Robust Classification using Contractive Hamiltonian Neural ODEs

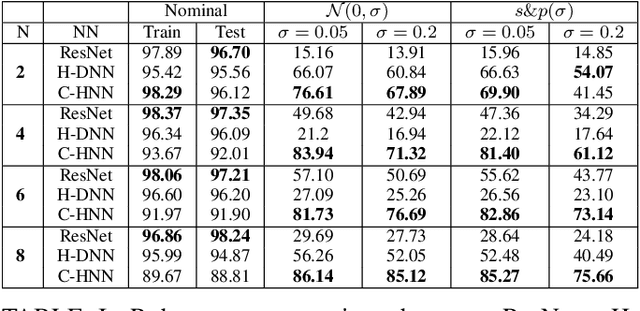
Deep neural networks can be fragile and sensitive to small input perturbations that might cause a significant change in the output. In this paper, we employ contraction theory to improve the robustness of neural ODEs (NODEs). A dynamical system is contractive if all solutions with different initial conditions converge to each other asymptotically. As a consequence, perturbations in initial conditions become less and less relevant over time. Since in NODEs, the input data corresponds to the initial condition of dynamical systems, we show contractivity can mitigate the effect of input perturbations. More precisely, inspired by NODEs with Hamiltonian dynamics, we propose a class of contractive Hamiltonian NODEs (CH-NODEs). By properly tuning a scalar parameter, CH-NODEs ensure contractivity by design and can be trained using standard backpropagation and gradient descent algorithms. Moreover, CH-NODEs enjoy built-in guarantees of non-exploding gradients, which ensures a well-posed training process. Finally, we demonstrate the robustness of CH-NODEs on the MNIST image classification problem with noisy test datasets.

Distributed neural network control with dependability guarantees: a compositional port-Hamiltonian approach

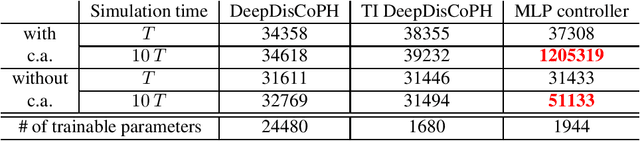
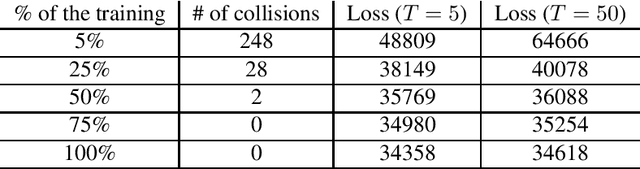
Large-scale cyber-physical systems require that control policies are distributed, that is, that they only rely on local real-time measurements and communication with neighboring agents. Optimal Distributed Control (ODC) problems are, however, highly intractable even in seemingly simple cases. Recent work has thus proposed training Neural Network (NN) distributed controllers. A main challenge of NN controllers is that they are not dependable during and after training, that is, the closed-loop system may be unstable, and the training may fail due to vanishing and exploding gradients. In this paper, we address these issues for networks of nonlinear port-Hamiltonian (pH) systems, whose modeling power ranges from energy systems to non-holonomic vehicles and chemical reactions. Specifically, we embrace the compositional properties of pH systems to characterize deep Hamiltonian control policies with built-in closed-loop stability guarantees, irrespective of the interconnection topology and the chosen NN parameters. Furthermore, our setup enables leveraging recent results on well-behaved neural ODEs to prevent the phenomenon of vanishing gradients by design. Numerical experiments corroborate the dependability of the proposed architecture, while matching the performance of general neural network policies.