Neural Port-Hamiltonian Models for Nonlinear Distributed Control: An Unconstrained Parametrization Approach
Paper and Code
Nov 15, 2024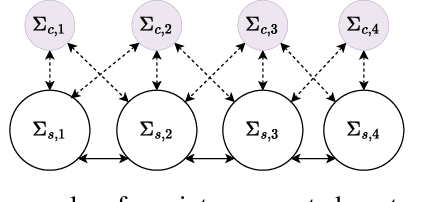
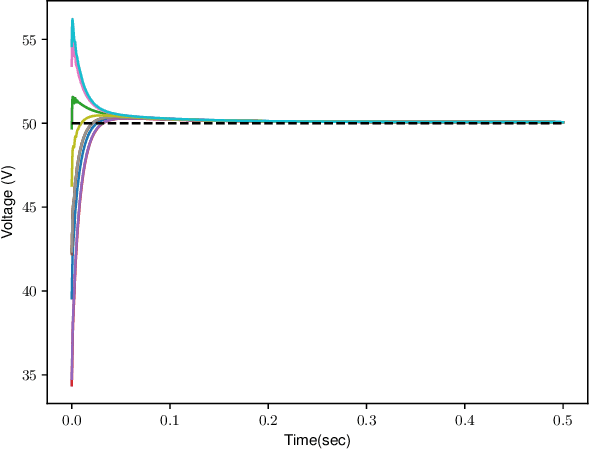
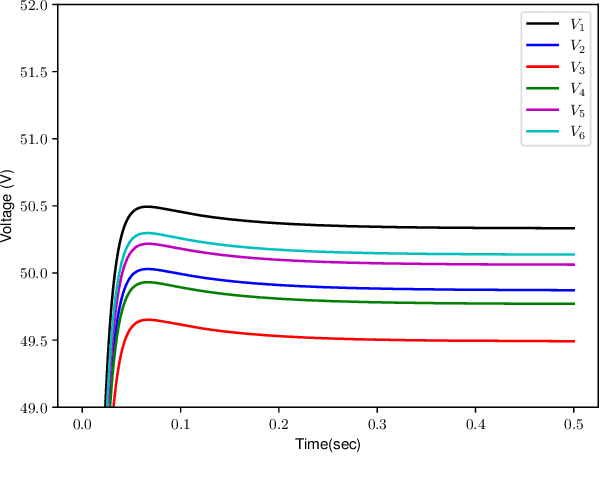
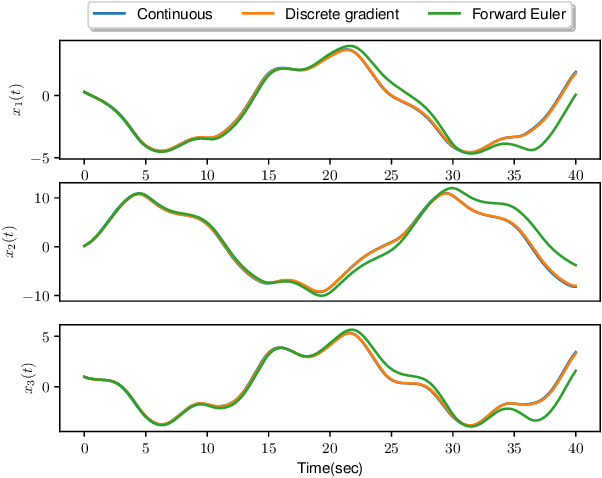
The control of large-scale cyber-physical systems requires optimal distributed policies relying solely on limited communication with neighboring agents. However, computing stabilizing controllers for nonlinear systems while optimizing complex costs remains a significant challenge. Neural Networks (NNs), known for their expressivity, can be leveraged to parametrize control policies that yield good performance. However, NNs' sensitivity to small input changes poses a risk of destabilizing the closed-loop system. Many existing approaches enforce constraints on the controllers' parameter space to guarantee closed-loop stability, leading to computationally expensive optimization procedures. To address these problems, we leverage the framework of port-Hamiltonian systems to design continuous-time distributed control policies for nonlinear systems that guarantee closed-loop stability and finite $\mathcal{L}_2$ or incremental $\mathcal{L}_2$ gains, independent of the optimzation parameters of the controllers. This eliminates the need to constrain parameters during optimization, allowing the use of standard techniques such as gradient-based methods. Additionally, we discuss discretization schemes that preserve the dissipation properties of these controllers for implementation on embedded systems. The effectiveness of the proposed distributed controllers is demonstrated through consensus control of non-holonomic mobile robots subject to collision avoidance and averaged voltage regulation with weighted power sharing in DC microgrids.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge